Учебное пособие Теории вероятностей и математическая статистика

Пример: По нормально распределённой выборке объёма п = 16 найдены xв 20,2 и s 0,8. Оценить доверительный интервал с

надёжностью γ = 0,95.

Решение. По таблицам распределения Стьюдента при γ = 0,95 и п

xв 19,774, xв

Следовательно,

Замечание. При n , а практически при n > 30, распределение Стьюдента переходит в нормальное распределение.

4.7.3 Интервальная оценка дисперсии нормального распределения

Рассмотрим выборку Х объёма п значений нормально распределённой СВ. Пусть параметры (m, σ ) нормального распределения неизвестны. Построить интервальную оценку дисперсии.

Используя элементы выборки x1, x2 ,..., xn , определим исправлен-

ную выборочную дисперсию s2 и введём в рассмотрение статистику

s2 (n 1)2

Данная величина распределена по закону хи-квадрат с (п – 1) степенями свободы.

(Распределение с п степенями свободы называется распределение суммы квадратов с п независимыми с.в., распределёнными по нормальному закону N (0,1))

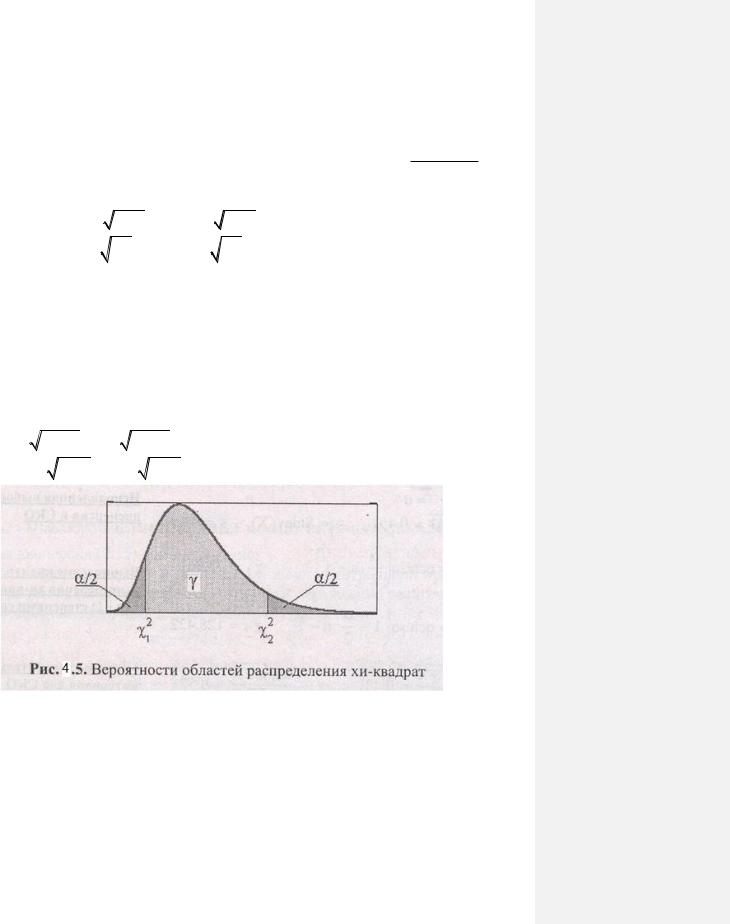
Для определения доверительного интервала задаём уровень значи-

вероятностью γ :

91

В ходе статистической обработки выборочной совокупности возникают предположения о тех или иных характеристиках генеральной совокупности (ГС). Речь может идти о виде предполагаемого распределения или, если закон распределения известен, о значении параметров этого распределения. Любое такое утверждение называют

статистической гипотезой.

Выдвинутое для проверки предположение называют основной или нулевой гипотезой Н0 .

Примеры основных гипотез

1.ГС распределена по а) нормальному закону; б) закону Пуассона;

2.Генеральная средняя равна а0; дисперсии 2-х распределений равны и т. д.

Вместе с основной гипотезой выдвигаются одна или несколько противоречащие ей гипотезы Н1 (Нr , r = 1,2 … ), которые называются

альтернативными.

Выдвинутая гипотеза называется простой, если она однозначно определяет параметр или вид распределения случайной величины. Гипотеза называется сложной, если она определяет некоторую область значений параметра. Например, гипотеза Н0: xB a0 – простая,

Н1: xB a0 – сложная.

В ходе статистической проверки гипотезы Н0 при данной альтернативной Н1 одна из них признаётся не противоречащей наблюдаемым данным, другая отвергается. Критерием значимости К для проверки статистической гипотезы является любое правило, определяющее выбор между гипотезами Н0 и Н1 в соответствие с наблюдаемыми значениями признака. Обычно такой критерий задаётся в виде некоторой функции выборки – K x1, x2 ,..., xn и, следовательно, является

случайной величиной. Чаще всего в качестве критерия используется статистика в виде нормированной нормальной величины, например, распределения хи-квадрат, Стьюдента, Колмогорова, Фишера и т. д.

Вычисляя по произведённой выборке значение критерия, которое называется наблюдаемым – Кнабл, мы делаем вывод о том, принимается или нет нулевая гипотеза, и тем самым отвергается или принимается альтернативная Н1. При этом вычисленное значение сравнивается с теоретическим, отвечающим уровню значимости, имеющему очень малую вероятность α.

93

4.8.2Критическая область. Алгоритм проверки гипотез

Суровнем значимости α тесно связана так называемая критическая область значения критерия К. Те значения К, при которых гипотеза

Н0 принимается, образует множество, которое называется областью принятия гипотезы (ОПГ). Всё остальное множество точек, на ко-

торых значения критерия Кнабл , вычисленного при условии истинности Н0 , равна уровню значимости α, называют критической областью (КО). Таким образом, ОПГ соответствует вероятности (1 – α) попадания в неё значения К. Различают одностороннюю (правосто-

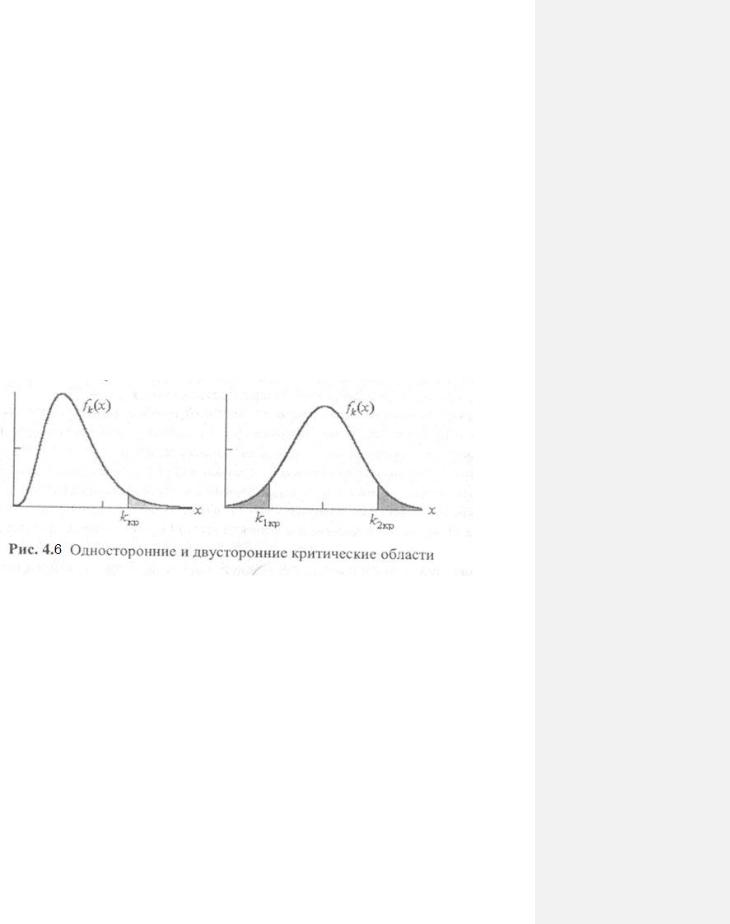
ронняя, если К > Kкр, интервал (Kкр , ), и левосторонняя, если К < Kкр, интервал ( , Kкр )) и двухстороннюю

(K Kкр1, K Kкп2 , Kкп2 Kкр1 ) критические области (см. рис. 4.6 ).

Алгоритм проверки гипотезы состоит из следующих этапов.

1. Формулируется нулевая Н0 и альтернативная Н1 гипотезы.

2.Задаётся уровень значимости α, значение которого обычно достаточно малым – обычно порядка 0,1 или меньше.

3.Выбирается статистика К критерия значимости, распределение которой известно.

4.Определяется тип критической области (односторонняя или двухсторонняя) и граничные значения Ккр.

5.На основе выборочных данных вычисляется наблюдаемое значение КВ.

94

6.Проверяется выполнение критерия. Если КВ попадает в критическую область, то нулевая гипотеза отвергается; если КВ попадает в допустимую область ОПГ, то считается, что данные вы-

борки не противоречат выдвинутой гипотезе Н0 и она принимается.

Возможные результаты проверки приведены в таблице. Поясним эти ситуации.

1.Вероятность отвергнуть проверяемую гипотезу Н0, когда она истинна. Эта вероятность как раз равна уровню значимости α.

2.Вероятность принять Н0 в случае, когда она истинна, и она рав-

на 1 – α.

3.Вероятность 1 – β означает, что отклоняется Н0, когда она ложна (т. е. истинна альтернативная гипотеза Н1 ).

4.Вероятность β есть вероятность того, что принимается гипотеза Н0, когда она ложна.

Вероятности α и β называются вероятностями ошибок первого и второго рода.

Ошибкой 1-го рода называется ошибка отклонения истинной гипоте-

зы Н0 .

Ошибка 2-го рода: отвергается альтернативная гипотеза Н1 , когда она на самом деле верна. Вероятность ошибки 1-го рода (равной α) называется уровнем значимости критерия. Чем она меньше, тем меньше вероятность отклонить верную гипотезу.

Величину 1 – β , т. е. вероятность недопущения ошибки 2-го рода называется мощностью критерии. Правильным решениям соответствуют недиагональные элементы таблицы (1 – α и 1 – β).

Примеры ошибок первого и второго родов.

1) Если отвергается истинное утверждение: «Студент Иванов заслуживает оценки 2», то он получает оценку «3» или выше – это

95

ошибка 1-го рода. Если же принимается ложное утверждение: «студент Иванов заслуживает оценки «2», то это ошибка 2-го рода.

2) Отвергнуто правильное решение: «продолжить строительство жилого дома» – ошибка 1-го рода, принято неверное решение: «продолжить строительство» – ошибка 2-го рода. Цена каждой ошибки зависит от конкретных условий.

Исследователю важно повысить вероятность правильных решений, т. е. одновременно уменьшить вероятности α и β. Однако попытка при том же объёме выборки уменьшить α будет приводить к увеличению вероятности β. Наоборот, при увеличении α вероятность β будет уменьшаться. Единственный способ улучшения обоих критериев – увеличение объёма выборки.

4.8.3 Проверка гипотез о виде распределения

Виды гипотез, которые приходится решать в статистике, можно разделить на два класса: гипотезы о параметрах распределения, которое приблизительно известно, и о характере самого распределения. Здесь мы рассмотрим вторую задачу.

При исследовании статистических данных по виду гистограмм можно сделать предварительное заключение о виде закона распределения. Здесь ставится задача с помощью критерия согласия подтвердить или опровергнуть характер распределения. Наиболее часто используются критерии согласия Пирсона и Колмогорова.

1) Критерий 2 (хи-квадрат) К. Пирсона

Пусть требуется проверить гипотезу Н0 о законе распределения с.в. Х с функцией распределения F (x). В качестве альтернативной гипотезы принимается положение, что гипотеза Н0 не выполняется. Для проверки используется выборка объёма п.

Всю область значений с. в. Х разбивают на m промежутков

с граничными точками x1 x2 ... xm 1 . В общем случае, когда значения с. в. занимают всю числовую ось, промежутки

i (i 1, m) соответствуют отрезкам ( , x1 ],(x1, x2 ],... (xm 1, ) . Подсчитывают вероятности рi (i 1, m) попадания в интервал , ис-

96

теза Н0 противоречит выборочным данным на уровне значимости α, и она отклоняется.

При практическом применении критерия Пирсона желательно, чтобы разбиения на интервалы проводилось таким образом, чтобы

– 8. Другие практические рекомендации заключаются в следующем. Первоначально находятся середины промежутков xi , которым

соответствуют заданные частоты ni . По этим данным определяются

Нормируют с. в. Х, т. е. переходят к вспомогательной с. в.

zi xi xв / в (4.13) с

соответствующей функцией распределения F(x) (для нормального распределения это будет функция N (0, 1)) и вычисляют теоретические вероятности рi попадания в интервал

97

i

Современная компьютерная техника позволяет вести расчёт по исходным формулам, например, в среде Mathcad или Excel. Однако если такого технического оснащения нет, то приходится пользоваться малой техникой, и тогда ручной счёт становится объёмным и утомительным. Для его облегчения можно воспользоваться следующим приёмом, который мы рассмотрим на примере.

Пример 1. При измерении размеров двухсот деталей получены следующие результаты, которые приведены в таблице

Выяснить, можно ли при уровне значимости α = 0,05 считать, что размер детали имеет нормальный закон распределения.

Решение. Для упрощения вычислений выборочных среднего и

тервала, С – константа, равная выборочной моде. Тогда выборочная средняя и дисперсия для с.в. Х через с.в. U запишется в виде:

ni (ui 1) niui2 2 niui ni ,

Подставляя сюда числа из последней строки таблицы, получим

200 – 40 + 482 = 642.

Из данных таблицы находим

находятся по таблицам нормированного нормального распределения, а pi по формулам (4.14). Первые и последние интервалы объединены, поскольку требуется, чтобы было ni > 5. В итоге получили 7 интервалов и число степеней свободы s = 7 – 3 = 4. По таблицам определяем критическое значение ̃ ( ) ̃ ( ) набл, из чего делаем заключение, что гипотеза о нормальном распределении размеров деталей принимается.

Можно найти максимальный уровень значимости, при котором это согласие имеет место. По таблицам находим максимальное значе-

Пример 2. ОТК проверил 200 партий одинаковых изделий и по-

изделий. При уровне значимости α = 0,05 проверить гипотезу о том, что число нестандартных изделий распределено по закону Пуассона.

Решение. По заданному распределению находим выборочную

Вычисляя по этой формуле вероятности Рi появления нестандартных изделий, а по ним – теоретические частоты, получим данные, по которым составим таблицу:

Аналогично проверяется критерий Пирсона и для других законов распределений непрерывных и дискретных случайных величин.

2) Критерий Колмогорова

Критерий Колмогорова является наиболее простым способом проверки гипотезы, но он ограничен тем, что применим только для

100