3.5. Каноническая форма уравнений Эйлера. Принцип максимума

Для задач оптимизации динамических систем, в частности, систем управления, применяют особую форму записи уравнений для определения допустимых экстремалей – с использованием функции Гамильтона. Эта форма получила наиболее широкое распространение для задач с дифференциальными связями и принята за основу в методах оптимизации систем при наличии ограничений в форме неравенств.

Рассмотрим задачу синтеза оптимального управления для объекта, модель которого задана в виде (2). Такая задача может рассматриваться как задача Лагранжа, причем модель объекта дает n дифференциальных связей (аргумент t в явном виде далее не учитывается для сокращения записи):

(19)

для которой далее записывают систему уравнений ЭйлераЛагранжа и применяют другие условия достижения экстремума.

Если дифференциальные связи приводятся к форме (2) или (17), может быть введена функция Гамильтона

Сравнивая выражения (19) и (20), нетрудно установить взамнооднозначное соответствие между функциями Лагранжа и Гамильтона:

Функции ψi(t) называются сопряженными переменными. Они могут быть определены по функции Гамильтона (20):

43

Запишем уравнения Эйлера-Лагранжа, учитывая (21):

Раскрыв скобки и продифференцировав, получим:

Система уравнений (22)...(24) называется системой уравнений Эйлера-Лагранжа в канонической форме.

Рассмотрим условия трансверсальности.

Для подвижных концов на основе (8) с учетом (20) получим:

При работе с функцией Гамильтона вместо (25), (26) обычно применяется следующее общее выражение для условий трансверсальности:

которое трактуется следующим образом:

–заключенное в скобки условие применяется как для левой t=t0, так и для правой t=t0 границ (концов временного интервала);

–если рассматриваемая граница задана, для нее вариация δt=0, если задано граничное условие xi0 или xi1, для данной границы и

44

соответствующего i вариация δxi=0, следовательно, все слагаемые в (27), содержащие такие вариации, тождественно равны нулю;

– для всех отсутствующих в задаче граничных условий соот-

ветствующие вариации δt и δxi являются ненулевыми и взаимно независимыми, следовательно, условие (27) будет выполняться только при равенстве нулю соответствующих сомножителей при вариациях, то есть при выполнении системы условий (25)...(26).

Рассмотренная система необходимых и достаточных условий достижения экстремума функционала в рамках вариационного исчисления обеспечивает получение локальных экстремумов. Этого вполне достаточно в задачах без ограничений на переменные состояния объекта управления или на управляющие сигналы. Если область допустимых управлений не ограничена, абсолютный экстремум совпадает с локальным. Если в задаче рассматривается некоторая ограниченная область допустимых состояний или управлений, задачу оптимизации нельзя свести к определению локального экстремума. Абсолютный экстремум в ряде случаев может совпадать с границей допустимой области.

Для задач с ограничениями используются специальные методы оптимизации, наиболее известными из которых являются принцип максимума Понтрягина и динамическое программирование Беллмана. Наиболее удобен для решения практических задач в силу своей простоты принцип максимума. Рассмотрим этот метод для задач с ограничением на управление.

Основная формулировка принципа максимума соответствует задаче обеспечения минимума функционала путем выбора оптимального управления в пределах некоторой области допустимых

управлений: U (t) C .

Для достижения минимума функционала (18) при заданных уравнениях объекта управления (17) необходимо достижение максимума функции Гамильтона по управлению

при фиксированных X и Ψ , соответствующих экстремуму, и соблюдении условий трансверсальности.

Следует подчеркнуть, что речь здесь идет о достижении абсолютного экстремума.

Отметим также важную особенность, определяющую удобство применения принципа максимума: уравнение (28) позволяет све-

45

сти задачу обеспечения минимума функционала к задаче обеспечения максимума функции Гамильтона как функции одной или нескольких переменных – составляющих вектора управления U. Предусматривается решение такой задачи для всех моментов времени в пределах рассматриваемого интервала.

Обычно область С определяется неравенствами

u jmin ≤ u j ≤ u jmax , j=1,2,...,r.

Оптимальное управление на основе (28) может быть получено

вследующих вариантах:

–как локальный экстремум внутри области C в соответствии с условиями (24);

–как абсолютный экстремум на границе области С ( u j = u jmin

или u j = u jmax );

– как кусочно-непрерывная функция, на отдельных временных интервалах совпадающая с границами, а на других – принимающая значения внутри области C.

В последнем случае для точек разрыва управления (при t=t*) следует учитывать недопустимость скачкообразного изменения переменных состояния объекта управления (условия припасовывания [2]):

0

уравнения связи x = u и ограничения на управление u ≤1.

Составим функцию Гамильтона H=–u2 –x+ψ1 u, уравнения Эйлера в канонической форме и условие трансверсальности:

∂∂Hx = −1, ∂∂Hu = −2u +ψ1 ;

ψ =1; 2u–ψ1 =0; ψ1 (0)=0.

Интегрированием первого уравнения с учетом условия трансверсальности получим: ψ1 =t+c1 , ψ1 (0) =c1 =0, ψ1 =t, u = t / 2 . Найденное управление соответствует локальному экстремуму, ко-

46

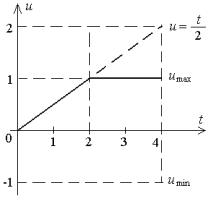
торый на интервале t [2; 4] выходит за пределы области допус-

тимых управлений (рис. 15).

Уравнение принципа максимума (28) позволяет учесть границы области допустимых управлений и определить характер экстремума.

В рассматриваемой задаче вектор управления содержит одну составляющую u, и зависимость H(u) имеет вид параболы, ветви которой направлены вниз. Вершина такой параболы, очевидно, соответствует максимуму функции H. Положение вершины параболы H(u) в рассматриваемом примере определяется полученной зависимостью u = t / 2 или

графиком на рис. 15. Следовательно, для интервала t [0; 2]

решение задачи достигается при u = t / 2 и с учетом вида графика параболы нетрудно установить, что для интервала t [2; 4] максимум H, т. е. ре-

Константы c1 и c2 определяются на основе граничного условия x(4)=0 и условия припасовывания x(2+ 0 )=x(2- 0 ). В результате

Значение достигаемого минимума функционала

47