
- •ВВЕДЕНИЕ
- •1. ПРИМЕРЫ И КЛАССИФИКАЦИЯ ЗАДАЧ ПРИНЯТИЯ РЕШЕНИЙ. ОБЗОР МЕТОДОВ
- •2. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕОРИИ ЭКСТРЕМАЛЬНЫХ ЗАДАЧ
- •2.1. Основные понятия
- •2.2. Порядок решения экстремальных задач
- •3. ДИНАМИЧЕСКИЕ ЗАДАЧИ ПРИНЯТИЯ РЕШЕНИЙ
- •3.1. Постановка задачи оптимального управления
- •3.2. Функционал, его свойства, необходимые и достаточные условия достижения экстремума
- •3.3. Вариационные задачи на безусловный экстремум
- •3.4. Вариационные задачи на условный экстремум
- •3.5. Каноническая форма уравнений Эйлера. Принцип максимума
- •3.6. Практические примеры применения принципа максимума
- •3.6.1. Синтез программы управления мягкой посадкой космического летательного аппарата
- •3.6.2. Синтез системы стабилизации, оптимальной по быстродействию
- •3.6.3. Расчетный пример
- •4. МАТЕМАТИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- •4.1. Линейное программирование: постановка задачи, основные понятия, графическая интерпретация
- •4.2. Симплекс-метод
- •4.2.1. Алгебраический вариант
- •4.2.2. Табличный вариант
- •4.3. Решение задач дискретного линейного программирования
- •4.4. Двойственная задача линейного программирования
- •4.5. Нелинейное программирование
- •4.5.1. Обобщенный метод множителей Лагранжа, условия Куна-Таккера
- •4.5.2. Численный метод зондирования пространства параметров
- •4.5.3. Методы безусловной оптимизации
- •4.5.4. Методы безусловной оптимизации первого и второго порядка
- •4.5.5. Прямые методы условной оптимизации
- •4.5.6. Непрямые методы условной оптимизации
- •4.5.7. Применение симплекс-метода для решения целочисленных задач нелинейного программирования
- •5. СТРАТЕГИЧЕСКИЕ МАТРИЧНЫЕ ИГРЫ
- •5.1. Основные термины и допущения. Формализация задачи. Принципы поиска решения
- •5.2. Общие методы решения стратегических матричных игр
- •5.2.2. Способы упрощения стратегических матричных игр
- •5.2.3. Решение стратегических матричных игр методом линейного программирования
- •5.2.4. Итерационный алгоритм Брауна-Робинсон
- •5.3. Примеры решения стратегических матричных игр
- •6. СТАТИСТИЧЕСКИЕ МАТРИЧНЫЕ ИГРЫ
- •Библиографический список
- •ОГЛАВЛЕНИЕ
Получим |
уравнение |
экс- |
|
|
|
|
|
|
|
|
||||||
тремали: |
|
|
x = t / 2 + c1 , |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = t2 / 4 |
+ c t + c |
2 |
. |
Исполь- |
|
|
|
|
|
|
|
|
||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
зуем |
граничное |
|
условие |
и |
|
|
|
|
|
|
|
|
||||
условия |
трансверсальности |
|
|
|
|
|
|
|
|
|||||||
для нахождения значения T и |
|
|
|
|
|
|
|
|
||||||||
уравнения допустимой |
экс- |
|
|
|
|
|
|
|
|
|||||||
тремали: |
|
|
x(0) |
= с1 = 0 , |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x(T)=T 2 / 4 + c2 , |
|
|
|
|
|
|
|
|
|
|
|
|
||||
− x(T) + x(T)+ 2x(T)= |
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= −T 2 / 4 +T + 2 T / 2 = 0, |
|
|
|
|
|
|
|
|
|
|
||||||
T=8, |
|
x(T)=82 / 4 + c2 =8 , |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c2= –8, x = t2 / 4 −8 . |
|
ука- |
|
|
|
|
|
|
|
|
||||||
Условие |
Лежандра |
|
|
|
|
|
|
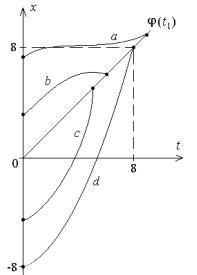
Рис. 14 |
||||||||
зывает на минимум. |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, на кривой |
|
|
|
(кривая d на рис. 14) |
||||||||||||
x = t2 / 4 −8 |
||||||||||||||||
обеспечивается минимум величиной |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
1 t2 |
|
t2 |
|
|
|
1 |
|
||
|
|
|
|
|
Smin = ∫ |
|
|
+ |
|
−8 |
|
|
|
. |
||
|
|
|
|
|
|
4 |
4 |
dt = 21 |
3 |
|||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|||
3.4.Вариационные задачи на условный экстремум
Ввариационных задачах на условный экстремум на функцию X, помимо граничных условий, накладываются дополнительные ограничения в форме некоторых уравнений (уравнений связи) или неравенств. Такие задачи наиболее часто распространены на практике. Так в задачах синтеза систем управления такими уравнениями являются уравнения объекта управления.
Наиболее просто учитываются ограничения в форме уравнений. Здесь аналогично задачам на достижение условного экстремума функции применяется принцип неопределенных множителей Лагранжа, развитый с учетом разновидностей уравнений связи в вариационных задачах. Общий подход состоит в том, что задача на условный экстремум функционала вида (3) сводится к задаче на безусловный экстремум нового функционала
35
t1 |
|
(11) |
J1(X)= ∫F1(X, X,t)dt , |
||
t0 |
|
|
причем вид функции F1 (функции Лагранжа) зависит от вида уравнений связи.
Рассмотрим основные виды таких задач.
Задача Лагранжа (задача с дифференциальными связями):
|
t1 |
|
|
|
обеспечить экстремум функционала |
J (X)= ∫ |
при |
||
f0 (X, X,t)dt |
||||
|
t0 |
|
|
граничных условиях xi (t0 )=xi 0 , xi (t1 )=xi 1 , i=1,2,...,n, причем допустимые кривые должны удовлетворять уравнениям связи
|
, j=1,2,...m<n. |
(12) |
g j (X, X,t)= 0 |
Условия (12) являются независимыми и не противоречат заданным граничным условиям.
Если хотя бы одно уравнение (12) содержит производную, такая задача называется задачей Лагранжа с дифференциальными связями. В частном случае, когда уравнения (12) имеют вид gj =gj (X,t), т. е. не содержат производных, имеем задачу Лагранжа с голономными связями.
Функция Лагранжа в задаче Лагранжа вводится следующим образом:
|
|
m |
|
(13) |
|
||||
F1(X, X,t)= f0 |
(X, X,t)+ ∑ψ j (t)g j (X, X,t), |
|||
j=1
где ψj (t) – произвольные функции времени, выступающие здесь как аналог неопределенных множителей Лагранжа в задаче обеспечения экстремума функции.
Экстремум функционала (11) ищут на основе рассмотренной в подразд. 3.3 системы необходимых и достаточных условий, причем при поиске допустимых экстремалей здесь возникает ситуация, когда имеется n+m неизвестных функций: xi (t), i=1,2,...,n
и ψj (t), j=1,2,...,m. Для их нахождения имеются m уравнений связи, а также n уравнений Эйлера-Лагранжа, составляемых дифференцированием функции F1. Отметим, что для получения ре-
зультата функции ψj находить, вообще говоря, не требуется, и в ряде конкретных задач их удается исключить в ходе решения.
Условия трансверсальности и Лежандра также применяются к функции F1.
36
Пример |
21. |
Обеспечить |
экстремум |
функционала |
|||
5 2 |
−t |
dt |
при граничных условиях x1 (0)=0, x2 (0)=1 с |
||||
J (x1, x2 )= ∫x2 e |
|
||||||
0 |
|
|
|
|
|
|
|
учетом уравнения связи x1 = x2 . |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
−t |
|
− x2 ). |
Составим функцию Лагранжа: F1 = x2 e |
|
+ ψ1(x1 |
|||||
Найдем частные производные и составим систему уравнений Эйлера-Лагранжа и необходимые условия трансверсальности (левый конец в задаче закреплен, правый подвижен):
∂F1 |
|
∂F1 |
|
|
|
|
|
∂F1 |
|
|
|
∂F1 |
|
|
−t |
|
|
|
||||
= 0 , |
|
|
|
= −ψ1 , |
= ψ1 , |
|
|
|
; |
= 0 , |
||||||||||||
∂x1 |
∂x2 |
|
|
|
|
|
|
|
|
= 2x2e |
|
−ψ1 |
||||||||||
|
|
|
|
|
|
∂x1 |
|
|
|
∂x2 |
|
|
|
|
|
|
||||||
|
− ψ1 − |
|
d |
|
|
−t |
)= 0 ; |
|
∂F1 |
|
|
|
|
|
= ψ1(5)= 0 , |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dt |
(2x2e |
|
|
|
|
t = 5 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
∂x1 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
∂F1 |
|
|
= 2x2 |
(5)e |
−5 |
= 0 . |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
∂x2 |
t = 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
После интегрирования ψ1 =c1 , |
|
|
|
|
−t |
= c1t + c2 . Применив ус- |
||||||||||||||||
2x2e |
|
|||||||||||||||||||||
ловия трансверсальности, получим c1 =0, c2 =0 и x2 = 0 . После-
довательно интегрируя последнее уравнение и уравнение связи, получим уравнения экстремали: x2 =c3 , x1 =c3 t+c4 .
С учетом граничных условий находим допустимую экстре-
маль: x1 = t , x2 =1 .
Составим матрицу (7) и проверим выполнение условия Лежандра:
F.. = |
|
0 |
0−t |
|
|
|
, ∆1 =∆2 =0. |
|
|
|
|||||
xx |
|
0 |
2e |
|
|
|
|
Вывод о характере экстремума сделать не удается. Тем не менее, с учетом неотрицательности интегранта значение функционала, доставляемое найденной допустимой экстремалью J=0, очевидно, является минимумом.
Таким образом, на кривой X = (t;1) обеспечивается минимум
величиной Smi n =0.
Изопериметрическая задача (задача с интегральными связя-
|
t1 |
|
|
ми): обеспечить экстремум функционала |
J (X)= ∫ |
||
f0 (X, X,t)dt |
|||
|
t0 |
|
37
при граничных условиях xi (t0 )=xi 0 , xi (t1 )=xi 1 , i=1,2,...,n, причем допустимые кривые должны удовлетворять уравнениям связи в форме интегральных уравнений:
t1 |
|
. |
|
|
|
|
|
j=1,2,...k. |
(14) |
∫G j |
X, X,t dt = wj , |
|||
t0 |
|
|
|
|
Отметим, что в отличие от задачи Лагранжа, количество уравнений связи здесь не ограничено.
Функция F1 вводится в данной задаче непосредственно в соответствии с принципом неопределенных множителей Лагранжа:
|
|
k |
|
(15) |
|
||||
F1(X, X,t)= f0 |
(X, X,t)+ ∑λ jG j (X, X,t), |
|||
j=1
где λj – произвольные постоянные коэффициенты.
Пример 22. Обеспечить экстремум функционала J (x)= 1∫x2dt
0
при граничных условиях x(0)=0, x(1)=1 с учетом уравнения свя-
1
зи ∫xdt = 0 .
0
Составим функцию Лагранжа: F1 = x2 +λ1x .
Найдем частные производные и составим уравнение Эйлера (концы в задаче закреплены, условия трансверсальности не требуются):
|
|
∂F1 |
= λ1 , |
∂F1 |
= 2x; λ1 |
−2x = 0 . |
|
|
|
|
|
|
|
||||
|
|
∂x |
|
∂x |
|
|
|
|
|
|
|
|
получим: |
x = λt / 2 + c1 , |
|||
Интегрированием |
уравнения |
|||||||
|
|
|
|
|
|
|
|
|
x = λt2 / 4 + c t + c |
2 |
. |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Уравнения экстремали в изопериметрических задачах содержат дополнительные константы – множители Лагранжа. Количество таких констант соответствует количеству уравнений связи, которые и используются вместе с граничными условиями или условиями трансверсальности для нахождения коэффициентов уравнения допустимой экстремали.
Применим граничные условия:
x(0)=c2 =0, x(1)=λ/4+c1 =1, λ=4–4c1 .
Подставим последнее выражение в уравнение экстремали: x=t2 -c1 t2 +c1 t, а результат – в уравнение связи:
38

1 |
(t2 |
−c t2 |
|
|
|
3 |
− c1t |
3 |
+ c1t |
2 |
|
1 = |
1 − c1 |
+ c1 = 0 , c1 = –2, |
∫ |
+c t)dt = t |
|
|
|
|
|||||||||
|
1 |
1 |
|
3 |
3 |
|
2 |
|
|
0 |
3 3 |
2 |
||
0 |
|
|
|
|
|
|
|
|||||||
λ=12.
Врезультате уравнение допустимой экстремали: x = 3t2 − 2t .
Проверим выполнение условия Лежандра: ∂2 F1 = 2 > 0 .
∂x∂x
Таким образом, на кривой |
|
|
обеспечивается мини- |
|
|
x = 3t2 − 2t |
|||
1 2 |
dt = |
1 |
2 |
|
мум величиной Smin = ∫x |
∫ |
(6t − 2) dt = 4 . |
||
0 |
|
0 |
|
|
Если в задаче одновременно присутствуют уравнения связи
(12) и (14), функция F1 |
вводится в форме |
|
|
|
||
|
|
|
m |
|
k |
|
|
|
|
||||
F1(X, X,t)= f0 |
(X, X,t)+ ∑ψ j (t)g j (X, X,t)+ ∑λ jG j (X, X,t). |
|||||
|
|
|
j=1 |
|
j=1 |
|
Для нахождения экстремума функционала к функции F1 применяются условия (5) ... (10) с учетом размерности задачи и полноты граничных условий.
Пример 23. Обеспечить экстремум функционала
5
J (x1, x2 )= ∫x22e−tdt при граничном условии x2 (0)= –2 с учетом
0
1
уравнений связи x1 = x2 , ∫x1dt =1.
0
Составим функцию Лагранжа: F1 = x22e−t +ψ1(x1 − x2 )+λ1x1 . Найдем частные производные и составим систему уравнений Эйлера-Лагранжа и необходимые условия трансверсальности (ле-
вый конец в задаче частично закреплен, правый подвижен):
∂F1 |
= λ1 |
, |
∂F1 |
= −ψ1 , |
∂F1 |
= ψ1 , |
∂F1 |
|
|
−t |
; |
|||||||
|
|
|
||||||||||||||||
∂x1 |
∂x2 |
|
|
|
|
|
= 2x2e |
|
||||||||||
|
|
|
|
∂x1 |
|
|
∂x2 |
|
|
|
|
|||||||
|
λ1 |
|
|
|
= 0 , − ψ1 |
− |
d |
|
|
−t |
)= 0 |
; |
|
|
||||
|
− ψ1 |
dt |
(2x2e |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂F1 |
t |
= 0 |
= ψ1(0)= 0 |
, |
∂F1 |
t =1 |
= ψ1(1) |
= 0 , |
|
|
||||||||
|
|
|
|
|
|
|||||||||||||
∂x1 |
|
|
|
|
∂x1 |
|
|
|
|
|
|
|
||||||
39
|
∂F1 |
|
= 2x2 (1)e |
−1 |
= |
0 . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
∂x2 |
t =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−t |
|
λ t2 |
|
После интегрирования ψ1 =λ1 t+c1 , |
2x2e |
|
= |
|
+c1t +c2 . |
|||||
|
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
Применив условия трансверсальности, получим c1 =0, λ1 =0,
c2 =0 и x2 = 0 .
Последовательно интегрируя последнее уравнение и уравнение связи, составим уравнения экстремали: x2 =c3 , x1 =c3 t+c4 .
С учетом граничных условий находим допустимую экстре-
маль: x1 = 2 − 2t , x2 = −2 .
Аналогично примеру 21 можно сделать окончательный вывод: на кривой X = (2 − 2t; − 2) обеспечивается минимум величиной
Smi n =0.
Задача Майера (задача управления конечным состоянием): найти векторную функцию X(t)=(x1 (t),x2 (t),…,xn (t)), удовле-
|
|
|
j=1,2,...m<n и |
творяющую уравнениям связи g j (X, X,t)= 0 , |
|||
граничным |
условиям xi (t0 )=xi 0 |
(i=1,2,...,n), xi (t1 )=xi 1 |
|
(i=2,3,...,n), |
значение первой составляющей которой при t=t1 |
||
максимально (минимально). Отметим, что начальные условия могут быть заданы полностью или частично. Примеры такой задачи приведены во введении (примеры 3,4).
Задача Майера сводится к задаче Лагранжа, например, пред-
ставлением |
x1 |
t1 |
и |
далее |
принимается |
(t1 )= ∫x1dt |
|||||
|
|
|
|
|
|
|
|
t0 |
|
|
|
t1 |
|
|
|
принцип |
Лагранжа в |
J (X)= ∫x1dt → max (min), применяется |
|||||
|
|
|
|
|
|
t0 |
|
|
|
|
|
форме (13), составляются уравнения Эйлера-Лагранжа, условия трансверсальности и т. д. Вернемся к примеру 3.
Пример 3 (формализация задачи Майера и переход к задаче Лагранжа). Введем переменные состояния, образующие вектор-
ную функцию X(t)=(x1 (t),x2 (t),x3 (t),x4 (t)): x1 =h, x2 =v, x3 =m, x4 =u. Уравнения связи примут вид:
x1 = x2 ,
40
|
x2 = |
cx4 |
− g , |
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|
x3 = −x4 . |
|
|
|
||
|
|
|
|
|
|
|
Заданы |
граничные условия: x1 (0)=0, |
x2 (0)=0, x3 (0)=m0 , |
||||
x1 (t1 )=H, |
t0 =0; значение t1 , а также остальные граничные усло- |
|||||
вия не заданы. Требуется обеспечить x2 (t1 )→ min . |
|
|
||||
Вводя критерий оптимальности в форме |
J (X) |
t1 |
, |
|||
= ∫x2dt → min |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
t0 |
|
получаем задачу Лагранжа.
Задача Больца: найти векторную функцию X(t)=(x1 (t),x2 (t),…,xn (t)), удовлетворяющую уравнениям связи
|
, |
j=1,2,...m<n, и граничным условиям |
g j (X, X,t)= 0 |
ϕl (t0 , X(t0 ),t1, X(t1 ))= 0 , l=1,2,...,k, которая доставляет экстре-
мум функционалу J (X)= t∫1 f0 (X, X,t)dt + Ψ(t0 , X(t0 ),t1, X(t1 )). От-
t0
метим, что в частных случаях граничные условия могут иметь вид, рассмотренный в предыдущих задачах.
Для перехода к задаче Лагранжа здесь вводится дополнительная составляющая вектора X
x |
(t)= ϕl (t0 , X(t0 ),t1, X(t1 )). |
(16) |
n+1 |
t1 −t0 |
|
|
|
Независимость функции (16) от времени t далее учитывается в форме дополнительного уравнения связи xn+1 = 0 . С учетом (16)
оптимизируемый функционал приводится к стандартному виду
t1 |
|
|
t1 |
|
|
|
J (X)= ∫ |
(t1 |
− t0 )= ∫[f0 |
]dt , |
|||
f0 (X, X,t)dt + xn+1 |
(X, X,t)+ xn+1 |
|||||
t0 |
|
|
t0 |
|
|
|
а на основе |
(16) вводится дополнительное |
граничное условие |
||||
xn + 1 (t0 )-xn + 1 (t1 )=0. |
|
|
|
|
|
|
|
Пример 24. Определить характеристический полином САУ, |
|||||||
|
T0 |
2 |
2 |
|
2 |
|
|
для которой функционал |
J (x)= ∫(a0 x |
)dt +αx |
(T0 )→ min . |
||||
|
+ a1x |
|
|||||
|
0 |
|
|
|
|
|
|
Заданы ненулевое значение x(0)=x0 , положительные a0, a1, α, конечное T0.
41

Обозначим исходную переменную x=x1 и введем дополнитель-
ную переменную |
x = αx2 |
(T |
)/ T |
. В задаче появится одно урав- |
|||
нение |
связи |
2 |
0 |
0 |
примет |
вид |
|
x2 = 0 , |
|
а |
функционал |
||||
|
|
|
|
|
|
|
|
J (x1, x2 )= T∫0(a0 x12 + a1x12 + x2 )dt .
0
Составим функцию Лагранжа, найдем ее производные, составим уравнения Эйлера-Лагранжа и условие трансверсальности:
F1 = a0x12 + a1x12 + x2 +ψ1x2 ;
∂F1 |
= 2a0 x1 , |
∂F1 |
= |
1, |
∂F1 |
= |
2a1x1 , |
∂F1 |
= ψ1 ; |
|||
|
|
|
|
|
|
|
||||||
∂x1 |
|
∂x2 |
|
|
∂x1 |
|
|
∂x2 |
|
|||
|
|
|
|
|
|
|||||||
|
1 − ψ1 = 0 , |
2a0 x1 |
−2a1x1 = 0 ; |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂F1 |
|
|
|
= 2a1x1(T0 )= 0 . |
|
|
|||||
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
||||||
|
∂x1 |
t =T0 |
|
|
|
|
|
|
|
|||
Отметим, что поскольку уравнение для x1 оказалось изолированным, первое дифференциальное уравнение решать не требуется и можно ограничиться только одним условием трансверсальности. Решение последнего уравнения дает общее выражение для
выходного сигнала САУ: x=x1 =c1 ek t +c2 e- k t , где k = 
 a0
a0  a1 . Применим граничное условие и условие трансверсальности:
a1 . Применим граничное условие и условие трансверсальности:
x(0)=c1 ek 0 +c2 e- k 0 =c1 +c2 =x0 ,
x(0)= c1kek0 −c2ke−k0 = c1k −c2k = 0 , c1=c2=x0/2.
Таким образом, здесь в отличие от примера 16 обе константы c1 и c2 оказываются ненулевыми, в выражении для выходного сигнала содержатся экспоненты как с отрицательным, так и с положительным показателем степени, а характеристический полином САУ должен иметь вид D(s)=(s+k)(s–k).
Отметим, что с точки зрения теории управления такая система является асимптотически неустойчивой [2]. Действительно, если работа системы рассматривается на ограниченном интервале времени, работоспособной и, как в рассмотренном примере, оптимальной может быть и неустойчивая с точки зрения классического предельного подхода система.
42
