На основе полученного решения задачи линейного программирования (табл. 46) получим решение игры, приведенной в табл. 42: V =1/ q = 5 (здесь, в отличие от (70), решалась задача обеспе-

Остается внести поправку в значение цены игры и записать решение исходной игровой задачи: V=5–5=0, P*=(0,25; 0,5; 0,25), Q*=(0,25; 0,5; 0,25).

5.2.4. Итерационный алгоритм Брауна-Робинсон

Приближенный численный метод решения игр основан на использовании итерационного алгоритма Брауна-Робинсон. Данный алгоритм предусматривает моделирование многократного повторения партий игры с выбором каждой из сторон для очередной партии чистой стратегии, обеспечивающей ей наилучший результат в условиях применения противоположной стороной наблюдаемой смешанной стратегии. Наблюдаемая, или опытная, смешанная стратегия рассчитывается по результатам проведенных партий игры. Установлено, что при увеличении количества смоделированных партий опытные стратегии сторон стремятся к оптимальным, а средний выигрыш стороны А – к цене игры.

Проследим работу алгоритма на основе примера 41. Матрица игры представлена в табл. 42.

Предположим, что для первой партии игры сторона А выбрала максиминную стратегию А1, сторона В – одну из минимаксных стратегий В2. В результате этой партии выигрыш стороны А составил «–3» единицы. Опытная стратегия стороны А описывается вектором P=(1; 0; 0), стороны В – вектором Q=(0; 1; 0).

Для второй партии игры сторона В выбирает чистую стратегию в условиях применения стороной А чистой стратегии А1. Очевидно, она придет к выводу о целесообразности сохранения стратегии В2. В свою очередь сторона А для второй партии выбирает чистую стратегию в условиях применения стороной В чистой стратегии В2. В этом случае наибольший выигрыш она сможет получить, перейдя к стратегии А2. Итак, сочетание стратегий сторон во второй партии игры А2В2, выигрыш стороны А во второй партии составит

146

4 единицы. Суммарный накопленный выигрыш стороны А по результатам двух партий игры равен единице, средний выигрыш за две партии составил 0,5.

После двух партий опытная стратегия стороны А описывается вектором P=(0,5; 0,5; 0), стороны В – вектором Q=(0; 1; 0).

Для третьей партии игры сторона В выбирает чистую стратегию в условиях применения стороной А опытной смешанной стратегии. Поэтому прогнозируемый результат для каждой из возможных чистых стратегий она должна рассчитывать усреднением соответствующего столбца матрицы игры с учетом опытных частот применения стороной А ее чистых стратегий – элементов полученного по предшествующим партиям вектора P. Наименьший ожидаемый проигрыш соответствует стратегиям В1 и В3. Примем для стороны В правило выбора в таких случаях стратегии с наименьшим номером.

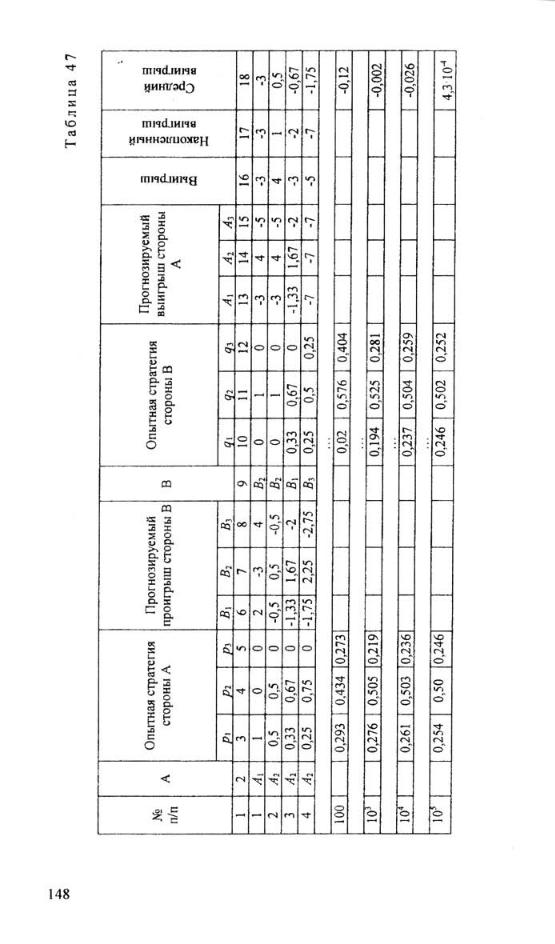
Результаты работы алгоритма на рассмотренных и последующих шагах подробно представлены в табл. 47.

В первом столбце таблицы приводится номер очередной партии, итог и накопленные результаты которой представлены в соответствующей строке. В столбцах 2 и 9 – чистые стратегии, примененные сторонами в очередной партии, в столбцах 3...5 – опытная смешанная стратегия стороны А после очередной партии, в столбцах 4...6 – ожидаемые проигрыши стороны В при различных ее чистых стратегиях в условиях применения стороной А такой опытной стратегии, в столбцах 10...12 – опытная стратегия стороны В, в столбцах 13...15 – ожидаемые выигрыши стороны А при различных ее чистых стратегиях в условиях применения стороной В текущей опытной стратегии, в столбце 16 – выигрыш стороны А, соответствующий сочетанию чистых стратегий из столбцов 2 и 9, в столбце 17 – суммарный (накопленный) выигрыш стороны А с учетом рассматриваемой партии, в столбце 18 – средний выигрыш стороны А в проведенных партиях игры (отношение накопленного выигрыша к номеру строки).

Представленные в табл. 47 результаты в сопоставлении с результатами решения рассматриваемого примера методом линейного программирования подтверждают возможность получения решения игры итерационным методом, причем точность результата, очевидно, определяется количеством смоделированных партий.

147