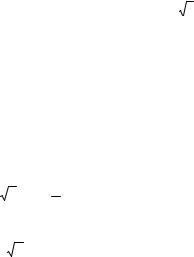
Рассмотрим статистику D

= D

(x , x ,...,x

n

) = n

sup

F (x)− F (x)

.

n

n

1 2

−∞<x<+∞

0

рия. При

n → ∞ критическое значение C совпадает с (1 − α) % кванти-

лью распределения Колмогорова.

При

практической

реализации

критерия

сначала

по

выборке

x , x

2

,..., x

n

составляют

вариационный ряд

x , x ,..., x .

Затем

находят

1

1

2

n

значение статистики

Dn . Для этого можно использовать несколько фор-

мул. Например,

i

i −1

Dn =

n max

− F0 (xi

), F0 (xi )

−

.

(5.6.5)

1≤i≤n n

n

Другая употребительная формула имеет вид

F0 (xi )−

2i −1

1

Dn =

n max

+

.

(5.6.6)

2n

2n

1≤i≤n

После этого сравнивают полученное значение Dn

с критическим зна-

чением C для заданного уровня значимости α и принимают или отвер-

гают гипотезу H0 .

Пример. Дано следующее распределение успеваемости 100 студен-

тов-заочников, сдавших четыре экзамена:

Число сданных

0

1

2

3

4

экзаменов

Число студентов

1

1

3

35

60

Проверить по критериям χ2 -Пирсона и Колмогорова гипотезу о том,

что

число сданных

экзаменов распределено

биномиально.

Принять

α = 0.1.

P(X = x) = C4x pxq4−x ,

x = 0,1,2,3,4 .

(5.6.7)

Для оценки вероятности

p

воспользуемся методом максимального

правдоподобия.

Получим

L(x1, x2 ,..., xk ) = P(X = x1 )×

× P(X = x

2

) ... P(X = x

k

) = C x1 p x1 qk −x1 C x2 p x2 qk −x2

... C xk p xk qk −xk =

k

k

k

= (Ckx1 + Ckx2 + ... + Ckxk

)p x1 +x2 +...+xk qk 2 −(x1 +x2 +...+xk ) =

= (Ckx1 + Ckx2

k

k 2

k

∑ x

− ∑ x

+ ... + Ckxk )pi=1 i q

i=1 i

. Найдем логарифм функции прав-

доподобия

k

k2

k

так как

k

k

k

i

∑xi

− ∑xi

2

2

p

=1

q

i=1

n

lnL = ln

=

∑Cni = 2n

= k ln2 + ∑xi ln p + k

−∑xi lnq .

i=1

i=1

i=1

∂ln

L

1

k

1

k

)

k

Тогда

∂p

=

∑xi −

k

2

− ∑xi

= 0 . Отсюда p = p

= ∑xi

k 2 .

p i=1

q

i=1

i =1

раз, т.е.

в

задаче

задана

сгруппированная

выборка.

Тогда

k

l

p =

∑xi

∑ximi

k 2 = sn

i=1

=

i=1

,

где

- число экзаменов,

сдаваемых всеми

k 2

sn

100 студентами,

s = 4

- число сдаваемых экзаменов,

n = 100 - число сту-

дентов, l

= 5

-

число

разрядов

сгруппированной

выборки.

Тогда

l

p =

∑xi mi

0

1 +1 1 + 2 3 + 3 35 + 4 40

i =1

=

= 0.88 .

Вычислим

теперь

sn

4 100

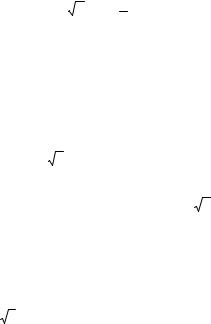
X

0-2

3

4

p

0.0732

0.3271

0.5997

Так как

F0 (x) =

∑ pi

, то гипотетическая функция распределения

xi <x

0,

x ≤ 2,

≤ 3,

будет равна F0 (x) =

0.0732, 2 < x

≤ 4,

0.4003, 3 < x

1,

x > 4.

Рассчитаем

теперь

значение

статистики

Dn

сначала

по

формуле (5.6.5)

i

i

−1

Dn

=

n max

− F0 (xi

), F0 (xi

)−

.

1≤i≤n n

n

1

− 0, 0

−

1 −1

= 0.3333,

i = 1 : max

3

3

2

1

i = 2 : max

− 0.0732, 0.0732 −

= 0.5935,

3

3

2

i = 3 : max 1 − 0.4003, 0.4003 −

= 0.5997.

3

Отсюда Dn =

3 max(0.3333, 0.5935, 0.5997) = 1.0387 .

При вычислении значения статистики по формуле (5.6.6) получим те

же

значения.

Действительно,

Dn =

n

F0 (xi )−

2i −1

1

max

+

,

1≤i≤n

2n

2n

i = 1 :

2 - 1

+

1 = 0.3333,

i

= 2 :

0.0732 -

3

+ 1 = 0.5935,

0 -

6

6

6

6

i = 3 :

0.4003 -

5

1

= 0.5997.

+

6

6

Dn =

3 max(0.3333, 0.5935, 0.5997) = 1.0387 .

Найдем

критическое

значение C критерия Колмогорова. Это 90% квантиль этого распределе-

ния, т.е. C = K −1(0.9) = 1.23 . Так как

D

< C ,

следовательно, D W \ ω