асимметрии более пологий склон многоугольника распределения наблюдается слева, в противном случае – справа. В первом случае асимметрию называют левосторонней, во втором – правосторонней.
Эксцессом или коэффициентом крутости называется число
E = |
μ4 |
−3 . |
(1.2.10) |
|
|||
|
σ4X |
|
|
Эта характеристика служит для сравнения на «крутость» данного и нормального распределения. Эксцесс для случайной величины, распределенной нормально, равен нулю. Если распределению соответствует отрицательный эксцесс, то соответствующий многоугольник распределения имеет более пологую вершину по сравнению с нормальной кривой. В случае положительного эксцесса многоугольник более крутой по сравнению с нормальной кривой.
1.3. Законы распределения непрерывных случайных величин
Непрерывной случайной величиной называется такая случайная величина, вероятность попадания которой в любую бесконечно малую область бесконечно мала и для которой при каждом x существует конечный или бесконечный предел
f (x) = lim |
P(x ≤ X < x + x) |
. |
(1.3.1) |
|
|||
x→0 |
x |
|
|
Все основные определения относительно закона распределения здесь остаются в силе. Для непрерывной случайной величины невозможно задать ряд распределения. Функция же распределения для нее существует и представляет собой непрерывную кривую.
Функцией распределения непрерывной случайной величины X называется вероятность следующего неравенства:
x |
|
F(x) = P(X < x) = ∫ f (t)dt |
(1.3.2) |
−∞ |
f (x) |
при условии, что существует такая неотрицательная функция |
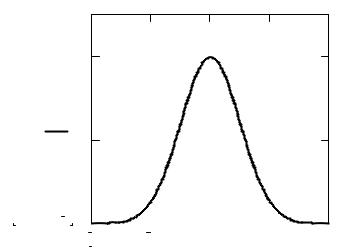
(рис. 1.2), интегрируемая в бесконечных пределах. Эта функция называется плотностью распределения вероятностей. Справедливы следующие соотношения:
9
0.5
0.4
f( x)
0.2
. |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1.338302 10 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
0 |
2 |
4 |
||||||
|
|
4 |
|
|
|
||||||||
|
|
4 |
|
|
|
|
|
x |
|
4 |
|||
Рис. 1.2. Функция плотности вероятности непрерывной случайной величины |
|||||||||||||
|
|
|
|
|
|
|
x |
f (t)dt, |
|
|
|
||
|
|
|
|
|
|
|
∫ |
|
|
|
|||
|
|
|
F (x) = |
|
|
|
(1.3.3) |
||||||
|
|
|
|
|
|
−∞ |
|
|
|
|
|||
|
|
|
|
f (x) = |
dF(x) |
. |
|
|
|
|
|||
|
|
|
|
|
dx |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функции плотности вероятностей соответствует кривая плотности распределения, или кривая плотности вероятности. Она является одной из форм закона распределения, но не универсальной, ибо существует только для непрерывной случайной величины. Ее некоторой аналогией для дискретных случайных величин является многоугольник распределения.
Свойства функции плотности распределения: 1. f (x) ≥ 0,
∞
2. ∫ f (x)dx = 1.
−∞
10
1.4. Числовые характеристики непрерывных случайных величин
Математическим ожидание непрерывной случайной величины X с плотностью вероятности f (x) называется
∞ |
|
M (X ) = mX = ∫xf (x)dx. |
(1.4.1) |
−∞
Все свойства математического ожидания, приведенные в предыдущих подразделах, остаются справедливыми и для этого определения. Еще две характеристики положения, а именно, мода и медиана остаются в силе для непрерывной случайной величины и даже определяются в этом случае наиболее естественным образом, если пользоваться понятием функции
плотности распределения. |
|
|
|
d X , |
|
Модой непрерывной случайной величины X |
называется число |
||||
определяемое как точка максимума функции плотности вероятности |
f (x). |
||||
Итак, |
|
|
|
|
|
f / (d X ) = 0, |
f / (x < d X ) > 0 и |
f / (x > d X )< 0. |
(1.4.2) |
||
Медианой непрерывной случайной величины |
X называется число |
||||
hX , удовлетворяющее условию |
|
|
|
|
|
h |
∞ |
1 . |
|
|
|
∫X |
f (x)dx = ∫ f (x)dx = |
|
(1.4.3) |
||
−∞ |
hX |
2 |
|
|
|
|
|
|
|
||
Все определения для начальных и центральных моментов остаются в силе, только суммы заменяются интегралами.
Дисперсией непрерывной случайной величины называется ее второй центральный момент, т.е.
∞ |
|
|
DX = D(X ) = ∫ |
(x − mX )2 f (x)dx. |
(1.4.4) |
−∞ |
|
|
Квантилью, или квантилем, |
порядка p распределения непрерывной |
|
случайной величины X называется число t p , удовлетворяющее условию
P(X < t p )= p или |
t p |
(x)dx = p . |
|
∫ f |
(1.4.5) |
||
|
−∞ |
|
|
Очевидно что, например, hX = t0.5 . |
|
|
|
Критической точкой порядка |
p распределения непрерывной случай- |
||
ной величины X называется число κp , удовлетворяющее уравнению
11
∞ |
|
P(X ≥ κp )= p или ∫ f (x)dx = p . |
(1.4.6) |
κ p
Квантили и критические точки одного и того же распределения связаны между собой простым соотношением κp = t1− p .
Асимметрия и эксцесс для непрерывных случайных величин определяются аналогично формулам (1.2.9) и (1.2.10).
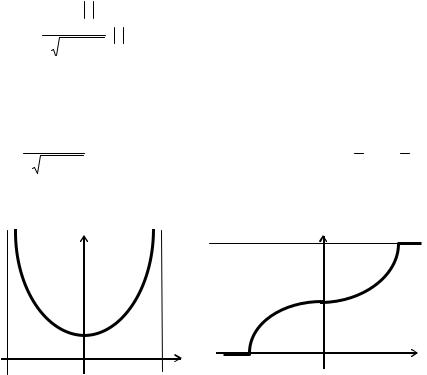
Пример. Случайная величина X подчинена закону арксинуса (рис. 1.3) с плотностью распределения вероятностей
|
|
0, |
x ≥ a, |
|
|
1 |
, x < a. Найти функцию распределения F(x) и вычис- |
f (x) = |
|
||
|
π |
a2 − x2 |
|
|
|||
лить mX , |
DX , |
d X , hX , κ0.75. |
|
|
Найдем |
сначала |
F(x). |
|
|
По |
определению |
|
|||||||||
x |
dt |
|
1 |
|
|
t |
|
x |
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||
= ∫ |
= |
|
|
|
|
|
|
|
|
|
|||||||
|
|
arcsin |
|
|
|
|
= |
|
|
arcsin |
|
+ arcsin1 |
= |
||||
|
π |
a |
|
|
|
a |
|||||||||||
−a π a2 − t 2 |
|
|
|
|
−a |
|
|
π |
|
|
|
||||||
|
|
|
|
|
|
||||||||||||
x
F(x) = ∫ f (t)dt =
−∞
12 + π1 arcsin ax .
Графики функции плотности вероятности и функции распределения приведены ниже.
f(x) |
F(x) |
|
|
|
|
0,5 |
|
1 |
|
|
|
|
|
|
|
|
|
πa |
|
|
|
|
|
|
||
-а |
|
а |
-а |
а |
|
|
|
||
Рис. 1.3. Графики функций плотности вероятности и распределения закона арксинуса
Определим теперь все числовые характеристики, необходимые по условию задачи.
12