Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский государственный технический университет "ВОЕНМЕХ" им. Д.Ф. Устинова

Предмет:

Теория вероятностей и математическая статистика

Файл:

Учебное пособие С.Д. Шапорев ПРИКЛАДНАЯ СТАТИСТИКА.pdf

Скачиваний:

596

Добавлен:

26.03.2015

Размер:

2.25 Mб

Скачать

☆

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 1516 / 3316 17 18 19 20 21 22 23 24 25 26 27 28 > Следующая >>>

5.2. Критерий Неймана – Пирсона

Если имеется некоторая выборка x1, x2 ,..., xn , то с помощью заданных ошибок первого и второго рода α и β можно решать задачу о наилучшем критерии. Именно по заданному значению уровня значимости α ищется такой критерий, чтобы его мощность 1 −β была максимальна. Введем

предварительно несколько обозначений и определений.

Размером α0 критерия называется максимальное значение вероятности ошибки первого рода при использовании данного критерия, т.е.

α0 = sup α(F(x)).	(5.2.1)
F (x) F

Равномерно наиболее мощным критерием заданного размера α0 на-

зывается критерий, имеющий среди всех критериев размера α0	наиболь-
шую мощность 1 −β =1 −β(F(x)) при любом распределении	F(x) F .

Равномерно наиболее мощные критерии существуют в крайне редких слу-

чаях, например, в случае простых гипотез H0 и H1 .				x1, x2 ,..., xn
Рассмотрим	две простые гипотезы	на	выборке	x1, x2 ,..., xn
H0 : F(x) = F0 (x)	и H1 : F(x) = F1(x), где	F0 (x)	и F1(x)	- известные

функции распределения. В этом случае равномерно наиболее мощный критерий называется критерием отношения правдоподобия и описывается следующим образом. Введем статистику


	Λ(x , x	2	,..., x	n	)=	L1	(x1, x2 ,..., xn )		,	(5.2.2)

	1					L0	(x1	, x2 ,..., xn )
где L0 (x1, x2 ,..., xn ) = f (x1)		f (x2 ) ... f (xn )						для непрерывной случайной
величины	X и L0 (x1, x2 ,..., xn ) = P(x1) P(x2 ) ... P(xn )									для дискретной.
Статистика	Λ(x1, x2 ,..., xn ) носит название отношения правдоподобия и

является отношением вероятностей (или плотностей распределения) получить выборку x1, x2 ,..., xn при условии справедливости гипотез H0 и H1 .

Естественно предположить, что чем больше отношение правдоподобия, тем большее предпочтение мы должны оказать гипотезе H1 . Об этом го-

вориться в лемме Неймана - Пирсона.

Лемма Неймана – Пирсона. Среди всех критериев заданного уровня значимости α, проверяющих две простые гипотезы H0 и H1 , кри-

терий отношения правдоподобия является наиболее мощным.

При практической реализации критерия отношения правдоподобия обычно удобно пользоваться не отношением правдоподобия, а его лога-

113

рифмом. В этом случае мы	должны принять гипотезу	H0 ,	если
Λ = Λ(x1, x2 ,..., xn )≤ C = ln C1 ,	и отвергнуть ее, т.е. принять	H1 ,	если

Λ > C . В соответствии с общим правилом уровень значимости α и мощность 1−β критерия отношения правдоподобия в зависимости от крити-

ческого значения C определяются по формулам:

α = α(C) = P(Λ(x1

, x2 ,..., xn ) > C H0 ) =

)dx dx

...dx

...

(x )

) ... f

Λ(x , x

∫ ∫

)>C

,..., x

P(Λ(x1

, x2 ,..., xn ) > C H1 ) =

β = β(C) =

(5.2.3)

= ∫...∫

(x1 )

(x2 ) ... f1(xn )dx1dx2...dxn .

Λ(x , x

,..., x

)>C

x1, x2 ,..., xn N(m, D)

Пример.

Пусть

H0 : m = a0 ,

H1 : m = a1 > a0 . Воспользуемся критерием Неймана – Пирсона. Крити-

ческая

область

для

гипотезы

определена

тогда,

когда

Λ(x1, x2 ,..., xn )> C .

(xi ) =

−

(xi −a0 )2

нашем

случае

2D ,

2πD

−a1)2

−a

n −

∑(xi

f (x ) =

e−

. Тогда Λ(x , x

)

2πD) e

i=1

,...,x

> C .

1 i

2πD

−

∑(x

−a

(1 2πD)n e

2D i=1

Упростим последнее выражение:

	1		n		)2−(x		)2
	1		∑(x	−a	)2−(x	−a	)2
e	2D		i	0	i	1
e		i=1						> C ,

∑n [(xi − a0 )2 − (xi − a1 )2 ]= ∑n (xi2

i =1

n	]> 2DlnC ,
∑[(xi − a0 )2 − (xi − a1)2	]> 2DlnC ,
i=1

− 2xi a0 + a02 − xi2 + 2xi a12 − a12 )=

		n					1		n
= 2∑xi (a0 − a1 )+ n(a02 − a12 )> 2D ln C ,							1		∑xi = mX =
= 2∑xi (a0 − a1 )+ n(a02 − a12 )> 2D ln C ,									∑xi = mX =
	i =1							n i =1
=	1		2D ln C − n(a02 − a12 ) = ϕ(C, D, a		0	, a ) = C .			Итак, m	> C , а так как
=			2D ln C − n(a02 − a12 ) = ϕ(C, D, a			, a ) = C .			Итак, m	> C , а так как
	n		2(a0 − a1 )			1	1		X	1
	n		2(a0 − a1 )
m		N(a		, D n), то можно по этому неравенству найти C , зная α, на-
X			i							1

114

пример,	m		− a	0	C	− a	0	=
пример,	α = P	X		0	> 1		0	=
			D n			D n
			D n			D n

2π

∞

∫

C1 −a0

−t 2	dt = 1	C		− a	0
e 2	dt = 1	− Φ	1		0	.
				D n
				D n

Таким образом, по α находится C1 из

	C	− a	0	= α. Кроме того,
1 − Φ	1		0	= α. Кроме того,
		D n
		D n

m		− a	C	− a	=
ства β = P	X	1 ≤	1	1	=
	D n			D n
	D n			D n

можно найти и β

Φ C1 − a1 . D n

решения уравнения

из аналогичного равен-

5.3. Проверка гипотез о числовых значениях параметров нормального распределения

Обозначим через X случайную величину, имеющую нормальный закон распределения с параметрами mX и DX , т.е. X N(mX , DX ), при-

чем числовые значения либо одного, либо обоих параметров неизвестны. Узнать, каково численное значение неизвестного параметра, можно, обследовав всю генеральную совокупность, что сделать, как правило, нельзя.

Обычно вместо этого проводят выборочные наблюдения, предполагая при этом, что они независимы и проводятся в одинаковых условиях. Тогда

1 n

несмещенными

оценками

являются

∑x

n i=1

)

∑(xi − mX )

. Затем приступают к проверке гипотез.

n −1i=1

1. Проверка

гипотезы

числовом

значении

математического

ожидания нормального распределения при известной дисперсии

Нулевая гипотеза здесь

H0 : mX = a0 , а альтернативная гипотеза мо-

жет

быть

сформулирована

трех

видах

H1 : mX = a1 > a0 ,

2) H1 : mX = a1 < a0 , 3) H1 : mX = a1 ≠ a0 .

Зададим уровень значимости критерия α, а так как DX

известна, то в

качестве

статистики

критерия

можно

взять

случайную

величину

z = mX − a0 .

Так как

mX N(a0 , DX n),

что было уже несколько раз

показано ранее, ибо xi N(a0 , DX ), то z N(0,1).

115

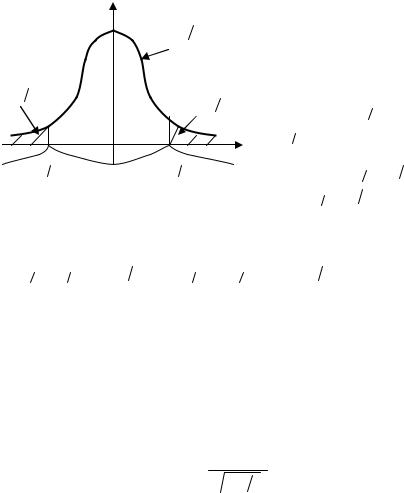
Выделим критическую область ω статистики z , при которой H0 отвергается. Размер и расположение критической области зависят от форму-

лировки

альтернативной

f (z H0 )

гипотезы. Рассмотрим 3-й

случай

H1 : mX = a1 ≠ a0 ,

здесь целесообразно выбрать

двусторонний

критерий

(рис. 5.6). Критическую об-

α 2

ласть образуют два интерва-

α 2

ла

(− ∞, zлев,α 2 )

(zпр,α 2 ,+∞).

Критические

W \ ω

точки определяются из ус-

tα 2

t1−α 2

ловий P(z < zлев,α 2 )= α 2 и

Рис. 5.6. Двусторонняя критическая область для

P(z > zпр,α 2 )= α 2 . Так как

матожидания

z N(0,1), то

критические

точки – это квантили нор-

мального

распределения

(см.

формулу

(1.4.5)),

т.е.

лев,α 2

= t

α 2

= Φ−1(α 2), а z

пр,α 2

= t

= Φ−1(1 − α 2).

1−α 2

Далее по выборке находим выборочное значение статистики критерия

zв

∑xi . Если zв ω , гипотеза

отвергается с уровнем значимо-

n i=1

сти α и принимается гипотеза

H1 . Если же zв W \ ω , то гипотеза

принимается.

2. Проверка гипотезы о числовом значении математического ожидания нормального распределения при неизвестной дисперсии.

В этом случае отличие от предыдущих формул и предположений будет касаться лишь статистики критерия z и ее распределения. Выберем в

качестве статистики величину z = (mX) − a0 ) . Как было уже показано

DX n

ранее (см. подразд. 4.7, п. 2), эта статистика имеет распределение Стьюдента с (n −1) - й степенью свободы, т.е. z Sn−1(t). Все остальные пунк-

ты проверки остаются без изменений. Например, если выбрана альтернативная гипотеза 2-го вида H1 : mX = a1 < a0 (рис. 5.7), критическая об-

ласть будет левосторонней, ее образует один интервал (−∞, zлев,α),

116

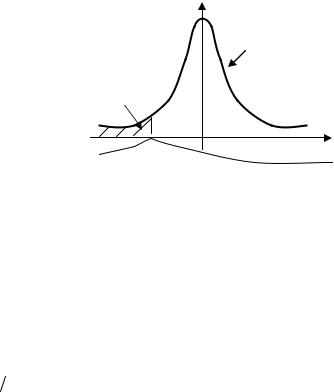
где точка zлев,α есть

квантиль распределения

sn−1(t)

Стьюдента. Он опреде-

ляется

из

условия

P(z < zлев,α = tα,n−1)= α

tα,n −1

или

∫s(t)dt = α, т.е.

−∞

tα,n−1 = S

−1

(α)

tα,n−1

W \ ω

Рис. 5.7. Левосторонняя критическая область

для матожидания

3. Проверка гипотезы о числовом значении дисперсии нормаль-

ного распределения.

Итак,

в этом случае известно, что X N(mX , D), но числовое значе-

ние дисперсии неизвестно. По выборке наблюдений x1, x2 ,..., xn

вычислим

)

точечные оценки mX =

∑xi

и DX =

∑(xi − mX )

и проверим ги-

n i=1

n −1i=1

потезу

H0 : DX = D0 , где D0 - заранее заданное число. В качестве стати-

стики

такой

гипотезы

следует

взять

случайную

величину

)

z =

DX (n −1) D0 . Ранее (см. подразд. 4.7) было показано, что эта случай-

ная

величина

имеет χ2 -распределение

n −1

степенью свободы, т.е.

z χn2−1 .

z и определения ее распределения все ос-

После выбора статистики

тальные вопросы проверки гипотезы носят технический характер. Зададимся уровнем значимости α, сформулируем альтернативную гипотезу и

перейдем к построению критической области и проверке H0 . Рассмотрим правосторонний критерий, т.е. альтернативная гипотеза должна быть

сформулирована в виде	H1 : DX > D0 , (рис. 5.8). Критическую область
образует один интервал	(zпр,1−α,+∞), где точка zпр,1−α есть 1 − α - про-
центный квантиль χ2 -распределения,		определяется из условия
P(z > zпр,1−α) = α или	∞
	∫kn−1(t)dt = α,	т.е. zпр,1−α = K −1(1 − α). Далее

zпр,1−α

117

<<< < Предыдущая 4 5 6 7 8 9 10 11 12 13 14 1516 / 3316 17 18 19 20 21 22 23 24 25 26 27 28 > Следующая >>>

Соседние файлы в предмете Теория вероятностей и математическая статистика