величины за точки |
|
χ12 |
|
и χ22 |
были одинаковы и равны |
α 2 = (1 − β) 2 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P(χ |
|
|
|
|
|
)= β . |
|
|
|
|
|
|
|
2 |
|
|
(n −1)DX |
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
2 |
|
|
2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
(рис. 4.3). Тогда |
P |
|
χ |
1 |
< |
|
|
|
|
|
|
< χ |
2 |
= 1 |
− P χ |
|
< |
χ |
1 ) |
− |
|
> χ |
2 |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
DX |
|
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Переворачивая |
неравенство внутри |
вероятности, |
окончательно |
|
будем |
||||||||||||||||||||||||||||||
|
|
|
) |
|
|
|
|
|
|
|
|
(n |
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(n −1)D |
X |
|
|
|
|
|
|
−1)D |
X |
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
||||||||
иметь P |
|
|
|
< D |
X |
< |
|
|
|
|
|
= β . |
Величины |
χ |
1 |
и χ |
2 |
находят |
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
χ |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
χ2 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
по таблицам |
χ2 -распределения |
|
из |
равенств P(χ2 > χ12 )= 1 − |
α |
= |
|
1 + β |
, |
||||||||||||||||||||||||||
|
2 |
|
|||||||||||||||||||||||||||||||||
P(χ2 > χ22 )= |
α |
|
1 − β |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||
= |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4.8. Лабораторная работа № 4. Оценивание параметров вероятностных распределений в пакетах STATGRAPHICS и MATHCAD
При построении оценок параметров распределений к ним предъявляются различные требования, такие как: несмещенность, эффективность, устойчивость к отклонениям от модели и тому подобное. Постоянно предлагаются новые концепции и подходы к оцениванию, а также конкретные алгоритмы их реализации. Свой вклад в разнообразие оценок вносят и различные способы параметризации распределений. Все это порождает множество различных оценок одних и тех же параметров. Поэтому трудно ожидать, что в том или ином статистическом пакете обязательно найдется процедура, в точности реализующая требуемый алгоритм. Однако почти все пакеты выводят значения наиболее распространенных оценок параметров стандартных вероятностных распределений.
В пакете STATGRAPHICS Plus for Windows большинство точечных оценок получается по методу максимального правдоподобия, а интервальные оценки для матожидания и дисперсии строятся точные. При этом в комментариях в StatAdvisor подчеркивается, что выборка должна быть взята из нормальной генеральной совокупности, иначе доверительные интервалы не точны и должны быть скорректированы.
Получим точечные и интервальные оценки для распределения Парето, описанного в подразд. 3.6. Для этого в начале смоделируем выборку этого распределения объемом в 100 единиц. Моделирование выборок псевдослучайных чисел в пакете STATGRAPHICS описано в лабораторной работе № 2 (подразд. 2.7). Для этого необходимо в головном меню пакета выбрать пункт Plot→Probability Distribution и в появившемся дополнительном меню отметить распределение № 18 – Парето. После
101
щелчка по кнопке ОК появится заставка распределения Парето. Функция плотности вероятности этого распределения равна
f (x) = α x0 (x0 x)α+1, x > x0 . В пакете автоматически задается x0 = 1,
таким образом, для полного определения распределения необходимо выбрать параметр формы α.
Щелкнем правой кнопкой мыши в любом месте заставки распределения Парето и в появившемся дополнительном меню выберем пункт Analysis Options. Зададим не пять, как позволяет пакет, а одно распределение с параметром формы (Shape), равным четырем. Далее в меню заставки распределения Парето выберем пункт Tabular Options и зададим в нем пункт Random Numbers. После щелчка по кнопке ОК будет автоматически смоделирована выборка псевдослучайных чисел, подчиненных распределению Парето, объемом 100 единиц. Сохраним эту выборку с помощью пункта меню Save Results под именем Pareto.
Для получения точечных и интервальных оценок параметров распределений в пакете STATGRAPHICS выберем в головном меню пункт Describe (Описание данных)→Numeric Data (Числовые данные)→OneVariable Analysis (Анализ одной переменной). Появится заставка дополнительного меню анализа одной переменной, в котором в окне Data необходимо указать имя выборки Pareto и нажать кнопку ОК.
Появится поле Analysis Summary (Сводка анализа). Выберем пункт дополнительного меню Tabular Options и зададим в нем вывод информа-
ции по разделам Analysis Summary, Summary Statistic (Описание данных) и Confidence Intervals (Доверительные интервалы). После щелчка по кнопке ОК на экран будет выведена информация, представленная на левой половине рис. 4.5.
Следует заметить, что по умолчанию пакет выводит значения лишь восьми общих статистик из девятнадцати. Если необходимы значения других точечных характеристик распределения, то их вывод на экран можно задать, щелкнув правой кнопкой мыши в поле Summary Statistics и выбрав пункт Pane Options дополнительного меню.
Аналогичный щелчок в поле Confidence Intervals и выбор пункта Pane Options вызывает дополнительное меню (рис. 4.4), которое задает величину доверительной вероятности
β (Confidence Level). По умолчанию
задается значение 95%. Выберем β = 99 и щелкнем по кнопке ОК. В
поле Confidence Intervals немедлен-
Рис. 4.4. Меню задания величины но изменятся границы точных дове-
доверительной вероятности
рительных интервалов для матема102
тического ожидания и стандартного отклонения. В пункте дополнительного меню Graphics Options отметим разделы Scatterplot (Диаграмма рассеи-
вания), Frequency Histogram (Частотная гистограмма) и Density Trace (График функции плотности). Тогда вид информации, выводимой на экран дисплея, будет полностью соответствовать изображенной на рис. 4.5.
Оценка параметра формы распределения Парето по методу максимального правдоподобия в пакете не находится, по элементам выборки этот параметр рассчитывается следующим образом:
|
|
|
|
|
|
|
) |
|
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
α = 1 |
|
|
∑ln xi |
− ln x0 . |
|
(4.8.1) |
||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
n i =1 |
|
|
|
|
||
|
|
Косвенно его можно оценить по оценке математического ожидания |
|||||||||||||
|
|
|
α |
|
|
|
|
|
|
|
|
) |
m |
|
|
m |
X |
= |
|
|
x |
|
, α > 1 , |
тогда, |
так |
как x = 1, то |
α = |
X |
= |
||
|
|
|
|
||||||||||||
|
|
α −1 |
|
0 |
|
|
|
|
|
0 |
|
mX −1 |
|||
=1.284351.28435−1 ≈ 4.52.
Впакете MATHCAD нет встроенных процедур оценок максимально-
го правдоподобия и построения доверительных интервалов, поэтому их придется программировать самостоятельно. Кроме того, в табл. 1 (см. подразд. 2.7) нет распределения Парето, следовательно, будем моделировать его по формуле (3.6.6) с использованием стандартных равномерных случайных чисел, получаемых по программам URAND или RUNIF (см. лабораторную работу №3, подразд. 3.6).
Сначала, так же как в пакете STATGRAPHICS, смоделируем выборку из генеральной совокупности с функцией распределения Парето объемом 100 единиц. Это можно сделать следующим образом.
|
1 |
t := runif (n,0,1) i := 1...100 |
|
|
|
1 |
c |
|
ORIGIN := 1 n := 100 x0 := 1 alfa := 4 c := |
d |
i |
:= x0 * |
|
||||
|
|
|||||||
|
alfa |
|
|
|
|
|||
|
|
|
ti |
|
||||
Mx := mean (d ) Mx = 1.375 Dx := var (d ) σx := 
Dx
Dx = 0.433 σx = 0.658
Получены точечные оценки матожидания и дисперсии. Оценка матожидания практически совпадает с аналогичной оценкой в пакете STATGRAPHICS, там Average=1.284. Дисперсия же значительно больше. Это связано с моделирующей формулой (3.6.6); если элементы выборки, полученной в пакете STATGRAPHICS, изменялись примерно от единицы до трех, то в пакете MATHCAD разброс элементов анало-
103
гичной выборки составляет от единицы до пяти, т.е. масштаб рассеивания значительно больше.
104
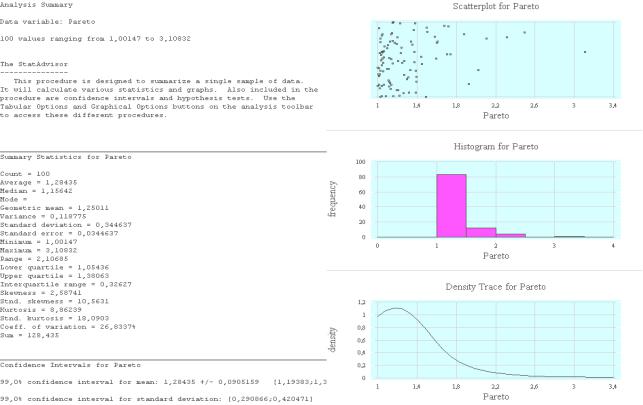
Рис. 4.5. Характеристики распределения Парето
Оценим теперь параметр формы α распределения Парето по методу максимального правдоподобия. Для этого составим функцию правдоподобия с учетом того, что x0 = 1:
|
L(x, α) |
|
n |
1 α+1 |
|
|
n |
|
1 |
α+1 |
|
|||||||
|
= ∏ |
α |
|
|
|
= αn ∏ |
|
|
. |
(4.8.2) |
||||||||
|
x |
|
x |
|||||||||||||||
|
|
i=1 |
i |
|
|
|
i=1 |
|
i |
|
|
|||||||
Логарифм функции правдоподобия |
α+1 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
|||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
= n ln α − (α +1)∑ln xi . |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ln L(x, α) = n ln α + ∑ln |
|
|
|||||||||||||||
|
∂ln L(x,α) |
|
|
|
|
|
i =1 |
|
xi |
|
|
|
|
i =1 |
|
|||
|
|
n |
|
n |
|
|
|
|
α) |
|
|
n |
|
|||||
Тогда |
= |
− ∑ln xi |
= 0 |
и |
= n ∑ln xi , т.е. |
получена |
||||||||||||
∂α |
|
|||||||||||||||||
|
|
α |
i=1 |
|
|
|
|
|
|
|
|
i =1 |
|
|||||
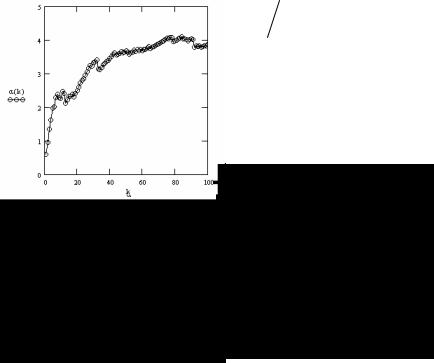
формула (4.8.1) с учетом x0 =1 . Вычислим в пакете MATHCAD логарифм функции правдоподобия и построим ее график:
n
LnL(α):= n * ln(α)− (α +1)* ∑ln(di ) i=1
k :=1...100 α(k ):= |
k |
α(10) = 2.262 α(50) = 3.697 α(100) = 3.865 |
|
∑ln(di )
i=1k
Построим, наконец, 99%-ные доверительные интервалы для математического ожидания и дисперсии, точечные оценки которых дают программы mean и var. Поскольку в пакете MATHCAD имеются встроенные функции для вычисления процентилей нормального распределения, рас-
пределения Стьюдента и χ2 - распределения, то легко строятся по форму-
лам подразд. 4.7 любые доверительные интервалы. Построим сначала приближенные интервалы.
105
β := 0.99 |
|
|
1 + β |
|
|
t1 = 2.576 |
ε := |
Dx |
* t1 |
||
t1 := qnorm |
2 |
|
,0,1 |
n |
|||||||
Mxl |
:= Mx − ε |
|
+ ε |
|
|
|
|
||||
Mxr := |
Mx |
Mxl = 1.205 |
Mxr = 1.544 |
||||||||
ε1 := |
2 |
* Dx * t1 ε1 = 0.158 |
|
Dxl := Dx − ε1 Dxr := Dx + ε1 |
|||||||
|
n-1 |
|
Dxr = 0.591 |
|
|
|
|
|
|
|
|
Dxl = 0.274 |
|
|
|
|
|
|
|
||||
Итак, доверительные интервалы, базирующиеся на предположениях ЦПТ, вычислены. Допуская, что выборка взята из нормальной генеральной совокупности (а наша выборка имеет распределение Парето!), построим «точные» интервалы.
t1 |
|
1 + β |
|
|
|
|
= 2.626 |
ε := |
Dx |
* t1 ε = 0.173 |
|
|
|
|
|||
:= qt |
2 |
, n t1 |
n |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
= 1.202 Mxr1 = 1.548 |
|
|
|
||||||
Mxl1 := |
Mx − ε |
Mxr1 := Mx |
+ ε Mxl1 |
|
|
|
|||||||||||
t1 |
|
1 − |
β |
, n |
|
= 66.510 |
|
|
1 |
+ β |
, n − |
|
= |
138.987 |
|||
:= qchisq |
2 |
|
−1 t1 |
t2 := qchisq |
2 |
1 t2 |
|||||||||||
|
|
|
−1) |
|
|
(n − |
1) |
|
|
|
|
|
|||||
Dxl1 := Dx * |
(n |
Dxr1 := |
Dx * |
Dxl1 = 0.308 |
Dxr1 = 0.644 |
|
|||||||||||
t2 |
|
|
t1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
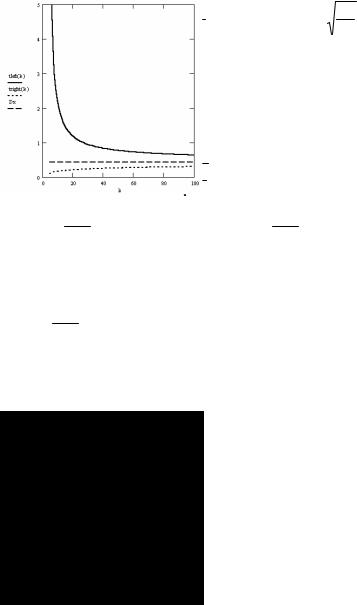
В заключение исследуем изменение длины точного доверительного интервала, например, для дисперсии в зависимости от объема выборки.
β1 := 1 −2 β k := 5...100
β2 := |
1 + β |
|
|
||||||
2 |
|
|
|
k −1 |
|
|
|||
|
|
|
|
|
|
||||
tright(k ):= Dx * |
|
|
|||||||
qchisq(β2, k −1) |
|
|
|
||||||
tleft(k ) |
:= Dx * |
|
k −1 |
|
|
||||
qchisq(β1, k −1) |
|
|
|
||||||
|
|
|
|
|
Задание №1. По номеру фами- |
||||
|
|
|
|
|
лии студента в журнале преподава- |
||||
|
|
|
|
|
теля выбрать распределение из |
||||
|
|
|
|
|
табл. 1 (если номер больше 16, вы- |
||||
|
|
|
|
|
бирать номер минус 15) и получить |
||||
|
|
|
|
|
точечные |
и интервальные |
оценки |
||
|
|
|
|
|
( β = 0.95 ) |
математического |
ожида- |
||
ния и дисперсии в пакетах STATGRAPHICS и MATHCAD. В пакете
MATHCAD, кроме того, по методу максимального правдоподобия оценить параметры выбранного распределения.
106