Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Балтийский государственный технический университет "ВОЕНМЕХ" им. Д.Ф. Устинова

Предмет:

Теория вероятностей и математическая статистика

Файл:

Учебное пособие С.Д. Шапорев ПРИКЛАДНАЯ СТАТИСТИКА.pdf

Скачиваний:

600

Добавлен:

26.03.2015

Размер:

2.25 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 3312 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

свойств, например, при некоторых условиях имеют минимальную дисперсию и тому подобное.

4.5.Методы получения точечных оценок

1.Метод моментов. Пусть имеется выборка x1, x2 ,..., xn из генеральной совокупности с теоретической функцией распределения F(x), при-

надлежащей k -параметрическому семейству F(x,θ1,θ2 ,...,θk ) с неизвестными параметрами θ1,θ2 ,...,θk , которые нужно оценить. Так как вид F(x)

известен, можно вычислить первые k теоретических моментов распределения, ибо формулы для этих моментов тоже известны. Эти моменты будут зависеть и от k неизвестных параметров θ1,θ2 ,...,θk :

	ν	= M (X )= ν			(θ ,θ		,...,θ	k	),
	1	= M (X	2	1	1	2		k
ν2		= M (X		)= ν2 (θ1,θ2 ,...,θk ),						(4.5.1)
										(4.5.1)
................................................
		= M (X	k	)= νk (θ1,θ2 ,...,θk ).
νk		= M (X		)= νk (θ1,θ2 ,...,θk ).

Суть метода моментов заключается в том, что так как выборочные моменты являются состоятельными оценками теоретических моментов, можно в системе (4.5.1) теоретические моменты ν1, ν2 ,..., νk заменить вы-

борочными ν1 , ν2 ,..., νk , а затем решить систему (4.5.1) относительно неизвестных параметров θ1,θ2 ,...,θk , т.е. найти оценки θ)1,θ)2 ,...,θ)k . Вместо

системы (4.5.1) реально приходится решать систему
	ν1 = ν1	(θ)1,θ)2		,..., θ)k ),
		)	)	)
	ν2 = ν2 (θ1		,θ2	,..., θk ),
................................................
		)	)	)

		(θ1	,θ2	,..., θk ).
	νk = νk

Часто получается, что найденные оценки θ)1,θ)2 ,..., θ)k

(4.5.2)

будут состоя-

тельными оценками θ1,θ2 ,...,θk . Справедлива следующая теорема об асимптотической нормальности оценок, полученных методом моментов.

		Теорема 4.2.	При некоторых условиях, наложенных на	семейство
F(		,θ1,θ2 ,...,θk ),	совместное распределение случайных	величин
	x
n (θ)1 −θ1), n (θ)2 −θ2 ),…, n (θ)k −θk ) при n → ∞ сходится к k -мер-

ному нормальному закону с нулевыми средними и ковариационной

матрицей, зависящей от теоретических моментов ν1, ν2 ,..., νk и матрицы ∂νi ∂θ j .

Практически моментами выше четвертого пользоваться нежелательно, так как точность их вычисления резко падает с увеличением порядка моментов. В методе моментов не обязательно использовать первые k моментов. Иногда в этом методе привлекают более или менее произвольные функции от элементов выборки.

Оценки, полученные методом моментов, имеют эффективность по Крамеру – Рао, существенно меньшую единицы, и могут быть смещенными. Но они часто используются из-за простоты получения, иногда в качестве начального приближения.

2. Метод максимального правдоподобия. Один из важнейших ме-

тодов для отыскания оценок параметров по данным выборки был предложен Р. Фишером и носит название метода наибольшего (или максимального) правдоподобия. Пусть имеется выборка объема n : x1, x2 ,..., xn из


генеральной		совокупности		с теоретической		функцией распределения
F(x). Если случайная величина					X , представленная этой выборкой, дис-
кретна, то ее ряд распределения					P(X = xi ), i =		. Пусть распределение
						1, n
имеет k	неизвестных параметров θ1, θ2 ,...,θk , которые нужно оценить.
Тогда	функция		L = L(x1, x2 ,..., xn , θ1, θ2 ,..., θk ) = P(x1, θ1, θ2 ,..., θk )×
× P(x2 , θ1, θ2 ,..., θk ) ... P(xn , θ1, θ2 ,..., θk ) называется функцией								правдо-
подобия.	Ее	значение –		это	вероятность	произведения		событий,

X = x2 ,…, X = xn , или, иначе, совместная вероятность появления чисел x1, x2 ,..., xn . Чем больше значение L , тем правдоподобнее или более вероятно появление в результате наблюдений чисел x1, x2 ,..., xn . Отсюда и

название функции – функция правдоподобия результатов наблюдений. Если наблюдаемая случайная величина X непрерывна, то функция правдоподобия имеет аналогичный вид, с той лишь разницей, что вместо вероятностей P(xi , θ1, θ2 ,..., θk ) фигурируют значения функции плотности

f (xi , θ1, θ2 ,..., θk ).

Метод нахождения оценок неизвестных параметров, основанный на требовании максимизации функции правдоподобия, называется методом максимального правдоподобия, а найденные этим методом оценки – оценками максимального правдоподобия.

Функции L или ln L , рассматриваемые как функции параметров θ = (θ1, θ2 ,..., θk )Τ , достигают максимума при одном и том же значении

параметра θ , так как ln L - монотонно возрастающая функция. Поэтому

вместо отыскания максимума функции L находят (что удобнее) максимум функции ln L . Функция ln L называется логарифмической функцией правдоподобия.

По этому методу за оценку параметров θ1 = θ1(x1, x2 ,..., xn ),

θ2 = θ2 (x1, x2 ,..., xn ),…, θk = θk (x1, x2 ,..., xn ) принимаются значения аргументов функции L или ln L , при которых вероятность получения

Lданных значений выборки максимальна. Очевидно, что для этого

необходимо

∂L ∂θ = 0

или

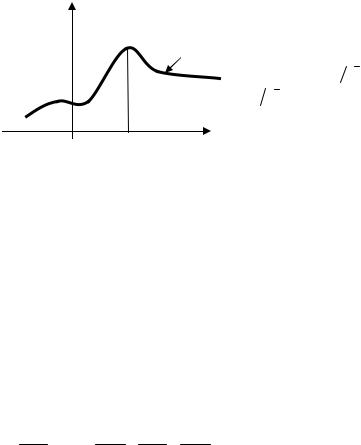
∂ ln L ∂θ = 0 . Решая эту в общем случае систему нелинейных урав-

)		нений, находят значения парамет-
θ	)	ров θ)	, θ)	2	,..., θ)	k	(рис. 4.1).
Рис. 4.1. Оценка параметра	θ на графике	1		2		k
Рис. 4.1. Оценка параметра	θ на графике	Пример. Найдем оценку мак-
функции правдоподобия		Пример. Найдем оценку мак-
		симального правдоподобия для ве-

роятности успеха в схеме Бернулли. Можно вероятность p рассматривать

как параметр, входящий в распределение дискретной двузначной случайной величины X , принимающей только два значения 1 и 0 в зависимости от того, появится ли рассматриваемое событие в текущем испытании или

не появится. Тогда P(X = m) = pm (1 − p)n−m , где n - количество испытаний, а m - число успехов в схеме Бернулли. Если m не фиксировать зара-

нее,

то

L = ∏ p zk (1 − p)1−zk ,

где zk = 0,1 - индикатор появления рас-

k =1

сматриваемого события,

= 1 , если это событие появится в

k -м испы-

тании и

= 0 , если не появится. Очевидно,

что

z1 + z2 +... + zn = m .

ln p +(1− z

)ln(1− p)] и

∂ln L

n z

− z

Тогда ln L =

∑

−

∑

−

)

∂p

∑

)

k =1

1− p

k =1

−

)

∑zk =

−

)

= 0 .

Здесь

∑zk .

Отсюда

1 − p k =1

1 − p

− p

n k =1

)

p = zk

∑zk

n k =1

Пример. Рассмотрим случайную величину X , подчиненную закону Пуассона с неизвестным параметром λ . Произведя выборку, получим наблюденные значения x1, x2 ,..., xn . Величина X может принять любое из

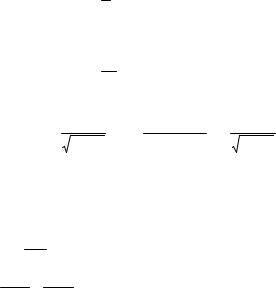
значений 0, 1, 2,… Так как P(X = x) = (λx x!)e−λ, x = 0,1,2,... , то функция

n	λ	x	k
правдоподобия имеет вид L(x1, x2 ,..., xn , λ) = ∏				e−λ	=
	xk !
k =1

λx1

e−λ

λx2

e−λ ...

λxn

e−λ

= e−nλ

Найдем производную функции

∑ xk

	λk =1					.
x	! x	2	! ... x	n	!
1
ln L			по	λ : ln L(x1, x2 ,..., xn , λ) =

n	n	∂ ln L		1	n	)	1	n
= ∑xk ln λ − nλ − ln ∏ xk ! ,			=	)	∑xk − n = 0 ,	λ =		∑xk .
		∂λ
k =1	k =1			λ k =1			n k =1

В заключение необходимо убедиться, что найденный стандартным методом матанализа экстремум – максимум. Представляем читателям сделать это самостоятельно.

Пример. Пусть величины xi , i =1, n имеют нормальное распределение. А неизвестных параметров два – матожидание и дисперсия. В этом случае

L(x

, x

,..., x

, m

, D

) =

∏

exp −

(xk − mX )

2πD

2DX

2πD

k =1

− m

× exp− ∑

, а ln L = −

(ln 2π + ln DX )−

∑(xk −mX )

k =1

x k =1

)

Для оценок

)

получим систему двух уравнений:

∂ln L

)

∂mX

)

∑(xk − mX ) = 0,

DX k =1

∂ln L

)

∂DX

= −

)

∑(xk − mX ) = 0.

2DX

)

Отсюда

∑xk

, а

∑(xk − mX ) .

n k =1

Метод максимального правдоподобия обладает важными достоинствами: он всегда приводит к состоятельным (хотя иногда и смещенным) оценкам, распределенным асимптотически нормально, имеющим наименьшую возможную дисперсию по сравнению с другими, также асимптотически нормальными оценками.

Однако далеко не для всех практических задач метод максимального правдоподобия дает удовлетворительные результаты. Дело в том, что предположение о принадлежности неизвестной плотности распределения

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 1112 / 3312 13 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете Теория вероятностей и математическая статистика