ления F(x) =1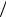
(1 + e−(x −μ)
λ ). После несложных преобразований методом обращения получается следующая моделирующая формула
x = μ − λln |
1 − ri |
, |
r R[0,1]. |
(3.6.15) |
|
||||
i |
ri |
i |
|
|
|
|
|
||
Задание № 1. По номеру фамилии студента в журнале преподавателя (если номер больше 15, считать номер минус 15) выбрать одно из рассмотренных пятнадцати распределений и смоделировать по соответствующим формулам выборку псевдослучайных чисел объемом 100 единиц. Построить график этой выборки. Для выборок, получаемых методом суммирования, определить эффект влияния количества слагаемых в теоре-
ме 3.2.
Стандартные равномерно распределенные случайные числа получать с помощью подпрограмм URAND или RANDU.
Смоделировать выборку такого же объема с помощью программ пакета MATHCAD (см. табл. 1), построить график этой выборки и сравнить оба полученных графика.
4. ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЙ И ИХ СВОЙСТВА
4.1. Статистические характеристики вариационных рядов и показатели их качества
Построив вариационный ряд и изобразив его графически, можно получить первоначальное представление о закономерностях в ряду наблюдений. Однако часто этого не достаточно. Поэтому для дальнейшего изучения изменения значений случайной величины используют числовые характеристики вариационных рядов. Поскольку эти характеристики вычисляются по статистическим данным, их обычно называют статистическими характеристиками или оценками.
Пусть по значениям измерений некоторой случайной величины требуется найти число, близкое к неизвестному значению измеряемого параметра. Например, пусть по значениям выборки объема n необходимо
оценить неизвестный параметр θ закона распределения случайной вели- |
|||||||
чины X P(X ≤ x) = F(θ, x). |
|
|
|
|
|
|
|
Точечной оценкой θ) неизвестного параметра θ |
|
называется произ- |
|||||
вольная функция элементов выборки θ) = f |
θ |
(x , x |
2 |
,..., x |
n |
). Значения этой |
|
|
1 |
|
|
|
|||
функции при полученных в результате измерений |
Xi = xi , i =1,2,...,n , |
||||||
будут считаться приближенным значением параметра θ . |
|
||||||
81 |
|
|
|
|
|
|
|
Любая функция результатов опытов, которая не зависит от неизвестных статистических характеристик, называется статистикой.
Точечной оценкой статистической характеристики θ (параметра) называется статистика, реализация которой, полученная в результате опытов, принимается за неизвестное истинное значение параметра θ .
Ясно, что статистика – случайная величина. Но не всякая статистика может быть оценкой θ . Чтобы статистика могла служить оценкой неизвестного параметра, необходимо, чтобы ее распределение было сосредоточено в достаточной близости от неизвестного значения θ . Оценка должна быть «хорошей», т.е. обладать рядом положительных качеств.
Показатель качества – это некоторая характеристика, определяющая соответствие оценки ее назначению, т.е. ее пригодность для получения решения поставленной задачи. Показатели качества могут измеряться в разных шкалах: количественных (шкала интервалов, отношений, абсолютных разностей), порядковых (шкала порядка, рангов, баллов), номинальных (шкала наименований). Показатели качества могут быть про- блемно-ориентированными, наиболее удобными, физически понятными при решении задач определенного класса, или универсальными, пригодными для различных классов задач. Количественные показатели могут быть представлены в абсолютных или относительных единицах. Для функциональных характеристик, представляющих собой функции f (θ)
некоторого аргумента θ , показатели могут быть локальными или глобальными. Локальные показатели характеризуют качество оценки f (θ)
при фиксированных значениях аргумента θ , а глобальные - вдоль всего диапазона изменения θ . Локальным показателем является, например,
дисперсия D(f (θ)), глобальным max D(f (θ)).
θ
Вся совокупность показателей качества может быть сгруппирована в четыре класса: функциональные, метрологические, технические и экономические (эффективности и эксплуатации).
4.2.Типовые принципы, используемые при построении оценок [5]
1.Принцип несмещенности π1 . Согласно этому принципу оператор
f , применяемый к выборке x , должен выбираться так, чтобы оценка θ) была несмещенной или асимптотически несмещенной, т.е.
M (θ))= θ или lim M (θ))= θ, θ F, |
(4.2.1) |
n→∞ |
|
где F - класс возможных оценок. Показателем качества в этом случае является значение смещения εθ) = M (θ))−θ. Чем меньше εθ) , тем качествен-
82
нее оценка и ее алгоритм. εθ) = 0 соответствует оптимальному по этому
показателю алгоритму.
2. Принцип состоятельности π2 . В качестве оценки следует выби-
рать состоятельную оценку, которая при неограниченном объеме выборки n сходится по вероятности к оцениваемой характеристике θ , т.е.
Pδ = P( |
) |
P |
|
θ − θ |
≤ δ)→1, δ > 0, n → ∞. |
(4.2.2) |
Не всякая состоятельная оценка несмещенная, но всякая состоятельная оценка, имеющая асимптотически конечное среднее, будет асимптотически несмещенной. Показателем качества здесь может быть, например, значение объема выборки n1 , начиная с которого Pδ меньше заданного
δ. Меньший объем выборки соответствует более качественной оценке.
3.Принцип минимума среднего квадрата отклонения (эффектив-
ности) π3 . Лучшей (более эффективной) считается та оценка, которая
имеет меньшее значение среднего квадрата уклонения (ошибки, квадратичного риска)
|
|
|
2 |
) |
2 |
|
2 |
|
2 |
|
|
2 |
→ min . |
(4.2.3) |
|||
|
|
|
|
||||||||||||||
|
σθ) |
= M (θ−θ) |
= ε |
θ) |
+σθ), |
σθ) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для каждой оцениваемой характеристики или параметра θ |
можно |
|||||||||||||||
попытаться найти нижнюю грань |
|
|
|
2 |
вдоль всех возможных операто- |
||||||||||||
|
|
|
|||||||||||||||
inf σ) |
|||||||||||||||||
|
|
|
|
|
|
|
|
f |
|
θ |
|
|
|
|
|
|
|
ров |
) |
, для которой достигается |
|
|
2 |
|
|||||||||||
|
|
|
|||||||||||||||
f . Оценка θ |
inf σ) , называется эффектив- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
θ |
|
ной.
4. Принцип минимума дисперсии или объема эллипсоида рассеи-
вания π4 . В тех случаях, когда смещение εθ) известно, его можно учесть
в результатах измерений. В других случаях оно может не влиять на результат. Тогда необходимо выбирать такой оператор f , который обеспе-
чивает минимум дисперсии σθ2) . Для несмещенных оценок это эквива-
лентно минимуму σθ2) = σθ2) . Для векторных параметров рассматривается минимум объема эллипсоида рассеяния. Можно попытаться найти ниж-
нюю грань дисперсии |
|
2 |
и соответствующий ей оператор f . Показа- |
inf σ) |
|||
|
f |
θ |
|
телем качества оценки θ) являются дисперсия оценки D(θ)) или дисперсия объема эллипсоида рассеяния или значение n1 , при котором обеспечивается требование к дисперсии оценки или к объему эллипсоида.
83
5. Принцип минимума ширины доверительных интервалов π5 .
Показатель качества таких оценок - значение ширины доверительного интервала. По этому принципу обычно конструируются интервальные оценки.
6. Принцип минимума меры близости π6 . Показатель качест-
ва – значение меры близости, например, d(θ,θ), 0 ≤ d ≤1 , причем
d (θ,θ)→ min . Условие предпочтительности оценки имеет вид
d(θ1 )≤ d(θ2 ).
7. Принцип извлечения максимума информации, содержащейся в выборке π7 . Выбираются такие алгоритмы и оценки, которые содержат в
себе максимум информации, имеющейся в выборке об измеряемой характеристике θ . Показателем качества оценки является значение разности информации, содержащихся в оценке и в выборке, например,
|
I (x,θ) |
|
|
|
|
|||
i(θ))= |
I (θ |
,θ) |
, |
i(θ))→ max . Условие предпочтительности i(θ) |
)≥ i(θ) |
|
). |
|
|
|
|
|
|||||
|
|
|
|
|
1 |
|
2 |
|
8. Принцип минимума потерь от использования оценки и про-
блемной ориентации π8 . Выбирается оценка, дающая меньшие потери,
если вместо истинного значения θ принимается θ) . Показателем качества могут быть абсолютные или отнесенные к наилучшей оценке значения средних потерь байесовского типа, различные показатели качества реше-
|
) |
R(θ) |
) |
|
ния |
r(θ)= |
inf R(θ)) |
, |
r(θ)→ min . |
f
9. Принцип асимптотической определенности π9 . Согласно этому
принципу асимптотические (при n → ∞ ) свойства оценок должны быть четко определенными, что обеспечивает метрологическую определенность измерения характеристик. Асимптотическая определенность может сводиться, например, к асимптотической нормальности оценок, их несмещенности, эффективности и тому подобное.
10. Принцип инвариантности по наблюдениям π10 или по изме-
ряемой характеристике π11 . Оценка θ) называется инвариантной по наблюдениям, если для любого взаимно однозначного отображения f (X )
имеет место равенство θ)(x)= θ)(f (x)). Оценка θ) называется инвариантной по измеряемой характеристике θ , если для произвольной однозначной функции f выражение f (θ)) есть оценка для f (θ) той же структуры, того
же типа, что и оценка θ) .
84