Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования

«Балтийский Государственный Технический Университет «Военмех» им. Д.Ф. Устинова»

Курсовая работа по прикладному программированию по теме

«Решение дифференциальных уравнений численными методами»

Выполнил: студент Н111

Макурова В.В.

Проверил: доцент каф. Н1

Жуков Ю.А.

Санкт-Петербург

2012

Оглавлени

Техническое задание 3

Описание модели исследуемого объекта 4

Математическое описание методов интегрирования для уравнения динамики системы тел 5

Описание программы на C++ 8

Краткое описание программы в пакете Matlab и представление результатов ее выполнения 10

Описание программы в Matlab 10

Выводы 13

Оглавление 2

Техническое задание 3

Описание модели исследуемого объекта 4

Математическое описание методов интегрирования для уравнения динамики системы тел 5

Описание программы на C++ 8

Краткое описание программы в пакете Matlabи представление результатов ее выполнения 10

Выводы 13

Техническое задание

Описать физический процесс с помощью системы дифференциальных уравнений второго порядка. Разработать программу в среде C++BuilderXE2, реализующую математическое моделирование физического процесса, а также решение дифференциальных уравнений тремя методами — Эйлера, Рунге-Кутта, Адамса. Сравнить результаты, полученные тремя методами. Выполнить проверку в математическом пакетеMatlab.

Описание модели исследуемого объекта

В качестве физического процесса рассмотрим движение тележки с двумя пружинами по бокам и пружинным маятником, закрепленным сверху, внутри коробки (см. рис.1).

Рис.1. Схематическое изображение системы

Процесс описывается тремя дифференциальными уравнениями в форме Коши:

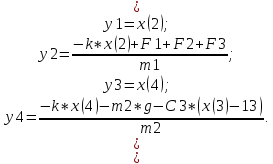(1.1)

Где

m 1 – масса нижнего тела (тележки);

m 2 – масса верхнего тела (груза);

C1 – жесткость левой пружины;

C2 – жесткость правой пружины;

C3 – жесткость верхней пружины;

l1 –длина покоя левой пружины;

l2 – длина покоя правой пружины;

l3 – длина покоя верхней пружины;

w – длина нижнего тела;

h – высота нижнего тела;

k – коэффициент трения среды;

L – ширина всей площадки, на которой перемещаются тела;

nyu – коэффициент трения о поверхность

Математическое описание методов интегрирования для уравнения динамики системы тел

Обыкновенными дифференциальными уравнениями описывают задачи движения системы взаимодействующих материальных точек, сопротивление материалов и многое другое. Ряд важных задач для уравнений в частных производных также сводятся к задачам для обыкновенных дифференциальных уравнений. Таким образом, решение обыкновенных дифференциальных уравнений занимает важное место среди прикладных задач физики, химии, техники. Обыкновенные дифференциальные уравнения n-го порядка можно с помощью замены свести к эквивалентной системе n уравнений первого порядка.

Решить дифференциальное уравнение численным методом – значит для заданной последовательности аргументов х₀, х₁…, х_nи числа у₀, не определяя функцию у=F(x), найти такие значения у₁, у₂,…, у_n, что у_i=F(x_i)(i=1,2,…, n) и F(x₀)=y₀.

Таким образом, численные методы позволяют вместо нахождения функции У=F(x) получить таблицу значений этой функции для заданной последовательности аргументов. Величина h=x_k−x_k-1называется шагом интегрирования.

Рассмотрим некоторые методы.

1. Метод Эйлера

Метод Эйлера относится к численным методам первого порядка, дающим решение в виде таблицы приближенных значений искомой функции у(х). Он является сравнительно грубым и применяется в основном для ориентировочных расчетов. Однако идеи, положенные в основу метода Эйлера, являются исходными для ряда других методов.

Рассмотрим дифференциальное уравнение первого порядка 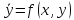с начальным условием x=x₀, y(x₀)=y_0.Найдём решения уравнения на отрезке [a,b]

Разобьем отрезок [a,b] наnравных частей и получим последовательность х₀, х₁, х₂,…, х_n, гдеx_i=x₀+ih(i=0,1,…,n), аh=(b-a)/n− шаг интегрирования.

В методе Эйлера приближенные значения у(х_i+1)≈y_i+1вычисляются последовательно по формулам:

y_i+1 = у_i+hf(x_i, y_i) (i=0,1,2…)

При этом искомая интегральная кривая у=у(х), проходящая через точку A₀(х₀, у₀), заменяется ломанойA₀A₁A₂… с вершинамиA_i(x_i,y_i) (i=0,1,2,…); каждое звеноA_iA_i+1этой ломаной, называемой ломаной Эйлера, имеет направление, совпадающее с направлением той интегральной кривой уравнения, которая проходит через точкуAi.

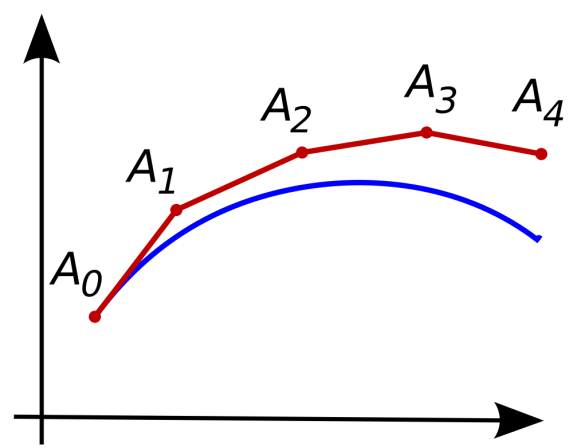
Рис.2. Ломаная Эйлера

Вычисления по методу Эйлера с пересчетом делаются в два этапа.

Прогноз:

Коррекция:

Модифицированный метод Эйлера с пересчетом имеет второй порядок точности, однако для его реализации необходимо дважды вычислять правую часть функции. Заметим, что метод Эйлера с пересчетом представляет собой разновидность методов Рунге-Кутты.

2. Метод Рунге-Кутты

Методы Рунге-Кутта обладают следующими свойствами:

1. Эти методы являются одноступенчатыми: чтобы найти у_к+1, нужна информация о предыдущей точке (x_к,y_к)

2. Методы согласуются с рядом Тейлора вплоть до членов порядка h^p, где степень р различна для различных методов и называется порядковым номером или порядком метода.

3. Они не требуют вычисления производных от f (x,y), а требуют вычисления самой функции.

Алгоритм Рунге-Кутта четвертого порядка:

Рассмотрим задачу Коши.

Приближенное значение в последующих точках вычисляется по формуле:

Вычисление нового значения проходит в четыре стадии:

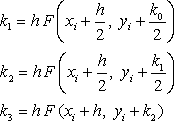
Этот метод имеет четвёртый порядок точности, то есть суммарная ошибка на конечном интервале интегрирования имеет порядок (ошибка на каждом шаге порядка).