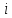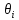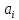- •2014 Оглавление
- •Постановка задачи и исходные данные
- •2. Формулировка последовательности согласованных систем координат. Кинематическая схема манипулятора
- •3. Расширенные матрицы перехода к системам координат, связанным со звеньями. Матрица манипулятора
- •4. Уравнение движения манипулятора. Прямая задача динамики
- •5. Регуляторы приводов манипулятора
- •5.1 Непрерывный пид-регулятор
- •5.2. Дискретный пид-регулятор
- •5.3 Регулятор с прямым расчётом момента
- •Приложения Приложение 1
- •Приложение 2
- •6. Литература
Балтийский государственный технический университет
«ВОЕНМЕХ» им. Д. Ф. Устинова
Кафедра Н1: Мехатроника и робототехника

ДОМАШНЯЯ РАБОТА
по дисциплине «Управление роботами и РТС»
Вариант 2
Выполнил: Евстифеев А. С.
Группа: Н101
Проверил: Жуков Ю.А.
Санкт-Петербург
2014 Оглавление
1.Постановка задачи и исходные данные 3
2. Формулировка последовательности согласованных систем координат. Кинематическая схема манипулятора 4
3. Расширенные матрицы перехода к системам координат, связанным со звеньями. Матрица манипулятора 5
4. Уравнение движения манипулятора. Прямая задача динамики 6
5. Регуляторы приводов манипулятора 12
5.1 Непрерывный ПИД-регулятор 12
5.2. Дискретный ПИД-регулятор 13
5.3 Регулятор с прямым расчётом момента 13
Приложения 15
Приложение 1 15
Приложение 2 18
6. Литература 21
Постановка задачи и исходные данные
По заданной кинематической схеме сформировать последовательность согласованных систем координат, связанных со звеньями манипулятора. Изобразить их на чертеже в исходном положении вместе с кинематической схемой манипулятора.
Составить расширенные матрицы перехода к системам координат, связанным со звеньями, и матрицу манипулятора.
Составить уравнения Лагранжа манипулятора и по нему вычислить обобщенные силы в сочленениях 1 и 2, реализующие заданную траекторию.
Решить прямую задачу динамики.
Вариант № 2 (ВПВ – 4)
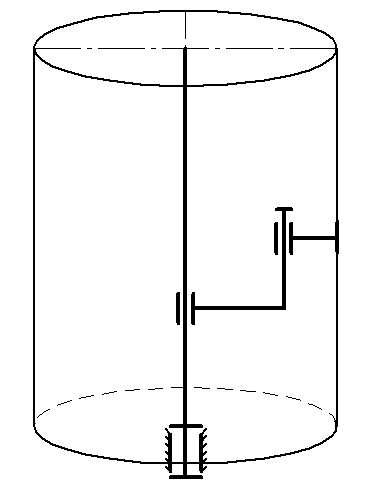
Рис.
1. Заданная кинематическая схема
манипулятора.
2. Формулировка последовательности согласованных систем координат. Кинематическая схема манипулятора
Последовательность согласованных систем координат сформируем в соответствии с представлением Денавита – Хартенберга. Для этого выполним следующие действия:
Формирование базовой системы координат (СК), связанной с основанием
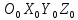 - ось
- ось направлена вдоль оси 1-го сочленения;
направлена вдоль оси 1-го сочленения;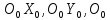 – произвольны.
– произвольны.Формирование i-ой СК, скреплённой с i-м звеном, при условии, что СК с № 0, 1, 2 … i-1 сформированы. Ось
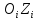 направлена вдоль оси движения
(вращательного и поступательного
направлена вдоль оси движения
(вращательного и поступательного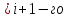 сочленения. Началоi
+ 1 - ой СК расположено на пересечении
осей
сочленения. Началоi
+ 1 - ой СК расположено на пересечении
осей
 и
и или на пересечении общей нормали к осям
или на пересечении общей нормали к осям и
и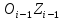 с
осью
с
осью Орт оси
Орт оси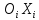 выбирается как
выбирается как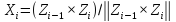 или вдоль общего перпендикуляра к осям
или вдоль общего перпендикуляра к осям и
и если они параллельны. Ось
если они параллельны. Ось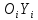 дополняет
дополняет и
и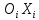 до правой тройки.
до правой тройки.Формирование СК схвата
 Ось
Ось направляется вдоль оси
направляется вдоль оси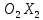 ;
точка
;
точка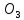 выбирается в геометрическом центре
схвата; ось
выбирается в геометрическом центре
схвата; ось направляется
в плоскости движения губок схвата
перпендикулярно
направляется
в плоскости движения губок схвата
перпендикулярно Ось
Ось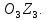 дополняет систему до правой тройки.
дополняет систему до правой тройки.
Кинематическая схема манипулятора в исходном положении и сформированные СК , связанные с его звеньями изображены на рис. 2.
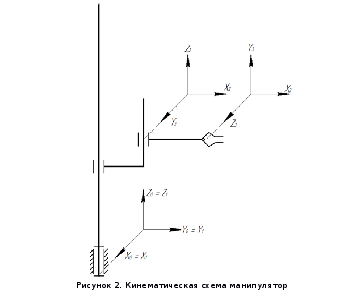
3. Расширенные матрицы перехода к системам координат, связанным со звеньями. Матрица манипулятора
Определим геометрические параметры звеньев в соответствии с представлением Денавита – Хартенберга.
 –присоединенный
угол – угол, на который надо повернуть
ось
–присоединенный
угол – угол, на который надо повернуть
ось
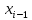 вокруг оси
вокруг оси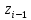 ,
чтобы она стала сонаправлена с осью
,
чтобы она стала сонаправлена с осью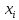 .
.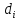 –расстояние
между пересечением оси
–расстояние
между пересечением оси
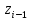 с осью
с осью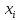 и началом
и началом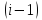 -й
системы координат, отсчитываемое вдоль
оси
-й
системы координат, отсчитываемое вдоль
оси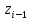 .
. –линейное смещение
– расстояние между пересечением оси
–линейное смещение
– расстояние между пересечением оси
 с осью
с осью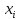 и началом -й системы координат,
отсчитываемое вдоль оси
и началом -й системы координат,
отсчитываемое вдоль оси ,
т.е. кратчайшее расстояние между осями
,
т.е. кратчайшее расстояние между осями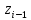 и
и .
. –угловое смещение
– угол, на который надо повернуть ось
–угловое смещение
– угол, на который надо повернуть ось
 вокруг оси
вокруг оси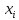 ,
чтобы она стала сонаправленной с осью
,
чтобы она стала сонаправленной с осью .
.
Введём в рассмотрение
обобщенные координаты звеньев
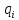 следующим образом:
следующим образом:
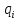 –угол поворота
звена
–угол поворота
звена
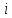 вокруг оси
вокруг оси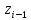 для всех
для всех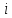 = 1,4,5,6;
= 1,4,5,6;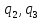 – смещение звена 2 вдоль оси
– смещение звена 2 вдоль оси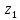 от начала базовой СК и смещение звена
3 вдоль оси
от начала базовой СК и смещение звена
3 вдоль оси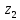 ,
соответственно.
,
соответственно.
|
Сочленение
|
|
|
|
|
|
1 |
|
0 |
0 |
0 |
|
2 |
|
|
|
0 |
|
3 |
0 |
|
|
|
Здесь
 – длина
– длина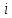 -го звена манипулятора (
-го звена манипулятора (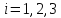 ).
).
По формуле (2.2-29)[1] определим ДХ-матрицы преобразования.
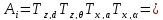

где
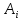 – матрица преобразования от
– матрица преобразования от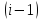 -й
к
-й
к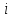 -й системе координат;
-й системе координат;
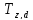 –однородная
матрица сдвига вдоль оси
–однородная
матрица сдвига вдоль оси
 на расстояние
на расстояние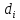 ;
;
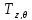 –однородная
матрица поворота вокруг оси
–однородная
матрица поворота вокруг оси
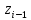 на угол
на угол ;
;
 –однородная
матрица сдвига вдоль оси
–однородная
матрица сдвига вдоль оси
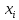 на расстояние
на расстояние ;
;
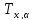 –однородная
матрица поворота вокруг оси
–однородная
матрица поворота вокруг оси
 на угол
на угол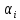 .
.
Таким образом,
при подстановке значений в формулу для
определения
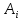 ,
находим
,
находим
A(:,:,1) = [ cos(q(1)) -sin(q(1)) 0 0
sin(q(1)) cos(q(1)) 0 0
0 0 1 0
0 0 0 1 ];
%=====================================================================
A(:,:,2) = [ 0 -1 0 0
1 0 0 L(2)
0 0 1 q(2)
0 0 0 1 ];
%=====================================================================
A(:,:,3) = [ 1 0 0 L(3)
0 0 -1 0
0 1 0 q(3)
0 0 0 1 ];