
Мороз_Электротехника
.pdf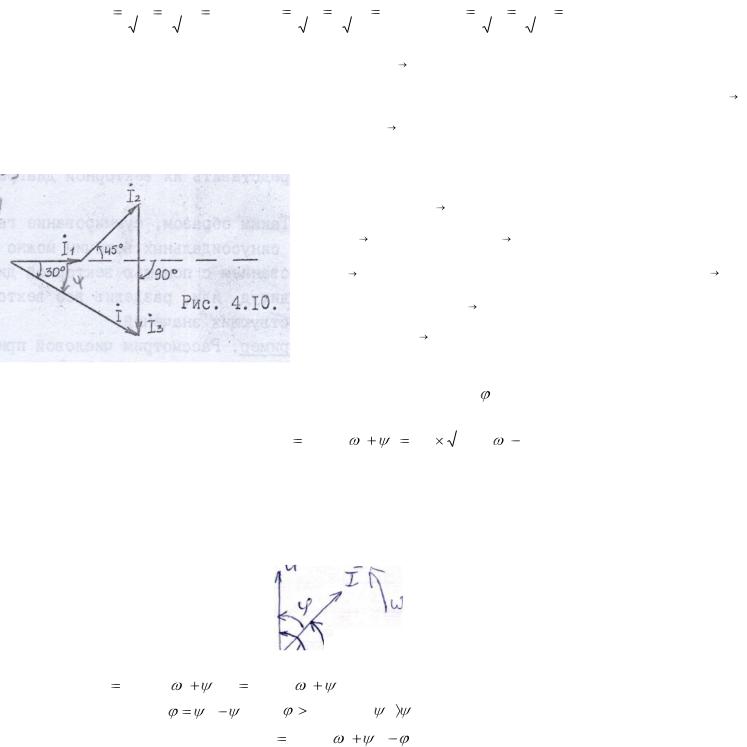
41
Сложение произведем при помощи векторной диаграммы. Определим действующие значения токов:
I1 |
I1m |
2,82 |
2A |
I 2 |
I 2m 4,23 |
3A |
I |
|
|
I3m |
5,64 |
|
3A |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
2 |
2 |
|
2 |
|
|
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Выбрав масштаб тока, переходим к построению векторной диаграммы. |
||||||||||||||||||||||||||||||||||
Сначала откладываем в масштабе ток I1 , направление которого (как первого |
||||||||||||||||||||||||||||||||||
вектора) выбираем произвольно (рис.4.10), |
|
далее |
|
|
из |
конца |
вектора |
I 1 |
||||||||||||||||||||||||||
откладываем в масштабе вектор тока I 2 |
, учитывая что по условию задачи он |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
опережает |
ток i |
|
|
на |
yгoл |
+450 |
(см.запись . |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
мгновенных |
значений токов |
i1 ; i2 |
; i3 ).Затем |
из |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
конца вектора I 2 |
|
откладываем в масштабе вектор |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
тока |
|
I 3 |
.Вектор тока I 3 согласно условию отстает |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
от |
I1 |
на угол 90°. Соединив конец вектора I 3 |
и |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
начало |
вектора |
|
I1 , получим результирующий |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
вектор тока |
I . |
Измерив величину этого вектора |
||||||||||||||||||||||
иучитывая масштаб, найдем действующее
значение общего тока I =4,6 А и угол сдвига его |
=-30°. |
||
Теперь можно написать мгновенное значение этого тока: |
|||
|
|
|
t 30 ) |
i I m sin( t ) 4,6 2 sin( |
|||
Для цепи состоящей из одного элемента, к которой приложено напряжение и ток в котором отстаѐт по фазе на угол  от напряжения,
от напряжения,
векторная диаграмма имеет вид:
U Um sin( t |
|
u ) i Im sin( t |
i ) |
|
|
||
Где угол |
U |
i |
, |
0 |
т.к. |
U |
i |
|
|
|
|
||||
|
|
|
|
|
|
|
|
Или можно записать: i |
Im sin( |
t U |
|
) |
|||
4.6. Синусоидальный ток в цепи с активным сопротивлением

42
На рис.4.11 приведена простейшая цепь, состоящая из одного активного сопротивления r . К зажимам цепи подведено синусоидальное напряжение U Um sin t Требуется определить мгновенное значение, тока i , действующее
значение тока I , мощность Р и построить векторную диаграмму.
Рис. 4.11
Мгновенное значение тока для данной цепи определяем по закону Ома, для этого мгновенное значение напряжения U разделим на сопротивление r
:
i =U/w |
(4.4) |
Подставляя вместо мгновенного значения u , его выражение, получаем :
i |
U m sin |
t |
I m sin |
t |
|
|
|
|
||||
r |
|
|
(4.5) |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
I m |
U |
m |
|
I |
I m |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r |
,где |
|
2 |
|
|||
- действующее значение тока Из выражения следует, что ток изменяется во времени по сину-
соидальному закону, как и напряжение U , причем в рассматриваемой цепи обе эти величины совпадают по фазе (рис.4.12).
На рис.4.13 показана векторная диаграмма тока и напряжения для этой
цепи
Мощность цепи синусоидального тока. Мгновенное значение мощности цепи синусоидального тока равно:
Pt Ui Um sin( t |
U ) Im sin( t |
i ) |
После преобразования получим:
|
|
P |
|
Um Im |
(cos( |
|
|
) |
cos(2 t |
|
|
)) |
|
||
|
|
|
|
U |
i |
U |
i |
|
|||||||
|
|
t |
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
P |
U m I m |
|
(cos |
cos(2 t |
|
)) |
UI (cos |
|
cos(2 t |
)) |
|||||
|
|
|
|
|
|
|
|||||||||
t |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||

43
 U
U  i -угол сдвига фаз между током и напряжением
i -угол сдвига фаз между током и напряжением
PUI(cos cos(2 t
cos(2 t  ))
))
Т.е. мгновенное значение мощности имеет две составляющие: постоянную UI cos - не изменяющаяся во времени, и переменную
- не изменяющаяся во времени, и переменную
составляющую UI cos(wt  ) -изменяющаяся по косинусоиде, колеблющаяся с двойной частотой относительно частоты тока (напряжения).Работа, совершаемая за один период Т частоты может быть выражена через среднее значение мощности:
) -изменяющаяся по косинусоиде, колеблющаяся с двойной частотой относительно частоты тока (напряжения).Работа, совершаемая за один период Т частоты может быть выражена через среднее значение мощности:
|
|
|
T |
|
|
|
Pcp |
T |
pdt |
|
|
|
|
|
0 |
|
|
T |
|
|
T |
T |
|
Pcp (1/ T ) |
pdt UI / T cos |
dt UI / T |
cos(2 t |
)dt |
|
0 |
|
|
0 |
0 |
|
Т.к. среднее значение за период косинусоиды двойной частоты равно |
|||||
нулю, то среднее значение мощности за один период Т=1: Pcp |
UI cos |
||||
Среднюю мощность Pcp |
называют |
активной |
, т.к. |
она характеризует |
|
интенсивность передачи энергии от источника к приемнику, т.е. идет активный процесс превращения электрической энергии в тепловую или механическую.
Для цепи , состоящей из элементов только c активным сопротивлением r,
cos 1 и |
|
|
P |
UI UI cos2 |
t |
Отсюда видно, что мгновенное |
значение |
активной мощности содержит |
постоянную сост. UI и переменную UIcos2 t , которые всегда положительные, т.к. cos2 t 0,и колеблется с двойной частотой:
Pcp UI , т.к. cos 1
1
Поскольку по закону Ома напряжение U R Ua 
может быть определена:
P U a I rI 2 U a 2 / r , (Вт)
4.7. Синусоидальный ток в цепи с индуктивностью L

44
Пусть электрическая цепь имеет только одну индуктивность (рис.4. 15) (об индуктивности было сказано ранее). На схеме принято по ГОСТу изображать индуктивность в виде трех полуокружностей, как на рис.4.15. Переменный синусоидальный ток создает переменное магнитное поле, которое по закону электромагнитной индукции индуктирует в витках ЭДС самоиндукции : eL = - L di/dt
Подставим значение производной от тока по времени:
eL |
L |
di |
|
LI m cos |
t |
LI m sin( t |
|
) |
|
|||
dt |
2 |
(4.7) |
||||||||||
|
|
|
|
|
|
|
|
|||||
Выражение (4.7) показывает, что ЭДС самоиндукции изменяется по закону |
||||||||||||
синуса и отстает от тока на |
угол |
|
П |
. |
Какое же |
напряжение необходимо |
||||||
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
подвести к зажимам цепи (рис.4.15), чтобы при наличии |
самоиндукции в ней |
|||||||||||
протекал заданный ток i |
Im sin |
t |
|
|
|
|
|
|
||||
На этот вопрос можно ответить, применив второй закон Кирхгофа. Для этого на схему (рис.4.15) наносим положительные направления напряжения, тока и ЭДС, принимая за положительное направление ЭДС, направление, совпадающее с током. Так как в цепи отсутствует сопротивление r согласно
второму закону Кирхгофа получим |
eL =U или |
|
||
U eL |
LI m cos t tI m sin( t |
|
) |
(4.8) |
|
||||
|
2 |
|
|
|
(если контур обходить по направлению тока).
Из выражения (4.8) видно, что напряжение приложенное к зажимам цепи, изменяется по закону синуса и опережает ток на угол [? Сравнивая выражения (4.7) и (4.8), видим, что напряжение по величине равно ЭДС самоиндукции и имеет противоположное направление.
Выражение (4.8) можно записать так:
U L U m sin( |
t |
|
) |
|
|
|
2 |
|
(4.9) |
||||
|
|
|
|
|
||
Где Um |
LIm |
|
xL Im |
|
|
|
|
|
|
||||
Разделив левую и правую части на |
2 |
получим: |
|
|||
|
|
|
U L |
xL I |
(4.10) |
|
|
|
|
|
|
|
|

45
Где xL , равное L, имеет размерность сопротивления: [wL]=Ом, и называется индуктивным сопротивлением.
Рассмотрим как соотносятся между собой ток и приложенное напряжение в цепи с одной индуктивностью. Для этого подведем к цепи синусоидальное
напряжение ,мгновенное значение |
которого U Um sin( |
t |
U ) .Для удобства и |
||||||||
простоты рассмотрения применим начальный угол U |
.Для рассматриваемого |
||||||||||
контура с L по второму закону Кирхгофа можно записать: U |
eL |
||||||||||
U m sin |
|
t ( |
L |
di |
) |
|
|
||||
|
|
|
|||||||||
|
|
|
|
|
|
|
|
dt |
|
|
|
|
di |
|
Um |
sin |
t |
|
|
||||
|
|
|
|
|
|
|
|||||
|
dt |
|
L |
|
|
|
|
|
|||
di |
U m |
sin |
tdt |
|
|
||||||
|
|
|
|||||||||
|
|
|
L |
|
|
|
|
|
|||
Найдем производную от тока по времени:
i |
T U m |
sin tdt |
|
|
U m |
cos |
t |
U m |
sin( t |
|
) ) |
||||||||||
0 |
|
L |
|
L |
|
L |
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
I m |
|
U m |
|
U m |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
t |
|
|
xL |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
i |
I m sin( |
t |
|
|
), |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
Где |
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда |
|
|
|
|
|
|
|
|
|
|
П |
90 |
|
|
|||||||
|
L |
u i |
u |
|
|
|
|
||||||||||||||
|
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
мгновенное значение мощности во времени:
P |
Ui U |
|
sin |
tI |
|
sin( t |
|
) |
|
Um Im |
sin 2 t UI sin 2 t |
m |
m |
|
|
||||||||
t |
|
|
|
|
2 |
|
2 |
|
|||
|
|
|
|
|
|
|
|
|
|||
Рис.4.15а |
Рис.4.15б |
На рис.4.16 показана векторная |
диаграмма напряжения, тока и ЭДС |
самоиндукции для электрической цепи, состоящей из одной индуктивности. На векторной диаграмме наглядно видно, что, ток отстает от напряжения на угол 90°. Можно сказать и иначе, что напряжение опережает ток на угол 90°, а ЭДС самоиндукции, в свою очередь, отстает от тока на 90 .
Мгновенное значение мощности:

46
Pt |
U i i U m sin tI m |
sin( t |
|
) UI sin t |
|
||||
|
|
2 |
|
|
На рис.4.17 показан график изменения тока, напряжения и мощности. В силу того, что ток отстает от напряжения ровно на
.17.
90°.
Мгновенная мощность изменяется за период четыре раза, причем если за первую четверть периода мощность положительна, то за вторую четверть она отрицательна. Это явление станет понятным из следующего. В первую четверть периода, когда ток и напряжение положительны (рис.4.17), мощность также положительна. Энергия от источника переходит в цепь в индуктивной катушке и затрачивается на создание магнитного поля в катушке. .
Во вторую четверть периода ток i убывает, но остается положительным. Напряжение U L и мощность QL отрицательны.
Энергия из магнитного поля катушки возвращается обратно в цепь. Таким образом, в индуктивности (когда r =0) происходит периодический обмен энергией между внешним источником и магнитным полем. Такая энергия обмена между источником и приемником электрической энергии, которая не преобразуется в другие виды энергии, называется реактивной энергией. Интенсивность обмена характеризуется реактивной мощностью:
QL U L I sin 
Средняя (активная) мощность такой цепи равна нулю. Полная мощность равна S=UI.Размерность полной мощности
[S]=B*A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. |
Катушка с индуктивностью L подключена к сети переменного |
|||||||||||||||
синусоидального |
тока с частотой |
f и напряжением U Um sin |
t . Определить |
|||||||||||||
действующее |
и |
мгновенное |
значение |
|
|
тока, |
индуктивное |
сопротивление |
||||||||
катушки и мощность, если f=50(1/C)Гц; L |
|
=0,0159Гн; U m =141 В. |
|
|||||||||||||
Решение. Определяем: индуктивное сопротивление |
|
|||||||||||||||
X L L |
2 fL |
2 3,14 50 |
0,0159 |
5Ом |
|
|
|
|
|
|
|
|
||||
Действующие значение напряжения: |
|
|
|
|||||||||||||
|
|
|
U |
U m |
141 |
100 |
В |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||

47
Действующие значение тока:
I |
U |
100 |
20 |
А |
||
|
|
|
||||
xL |
5 |
|||||
|
|
|
||||
Определяем мгновенное значение тока: поскольку в цепи только индуктивность, ток будет отставать от напряжения на угол П/2.Следовательно, мгновенное значение тока:
I = I m sin( t 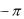 / 2) 20
/ 2) 20  1.41sin( t 2 )
1.41sin( t 2 )
Активная мощность P =0
S=UI=100*20=2000В*А Q=UI sin =2000 вар
4.8. Синусоидальный ток в цепи с активным сопротивлением r и индуктивностью L
Пусть имеем электрическую цепь, состоящую из активного сопротивления r и индуктивности L (рис.4.18), в которой протекает синусоидальный ток:
|
|
|
|
|
|
|
|
i |
I m sin |
t |
|
|
|
|
Требуется |
рассчитать |
такую |
цепь, |
|
т.е. |
определить |
приложенное к |
|||||||
зажимам напряжение, |
напряжения на участках U r ,U L |
потребляемую мощность и |
||||||||||||
пр. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Прежде всего нанесем на схему произвольно положительное направление |
||||||||||||||
тока. |
Положительное |
|
направление |
напряжения |
примем |
|||||||||
совпадающим с током и нанесем его на схему (рис.4.18). При про - |
||||||||||||||
хождении по индуктивности синусоидального тока в ней будет ин - |
||||||||||||||
дуктироваться |
ЭДС, |
|
которую |
на |
схеме |
также направим по направле- |
||||||||
нию |
тока. |
Напишем |
уравнение |
по |
второму закону |
Кирхгофа: |
||||||||
eL ri |
U ,откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
ri eL |
ri |
( L |
di |
) rI m sin |
t LI m cos t |
rI m sin t |
LI m sin( |
t |
|
) |
|||
|
|
|||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|
2 |
|
||
(4.11) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если выбрать обход цепи по направлению тока. |
|
|
|
|
||||||||||
Мгновенное |
значение |
напряжения |
U , приложенное |
к зажимам цепи, |
||||||||||
состоит из двух слагаемых |
U r |
и U L , |
где |
|
|
|
|
|
|
|||||
48
|
|
|
|
|
|
|
|
|
|
|
|
Ur |
rIm sin |
t , U L |
|
|
|
LI m sin( t |
|
|
|
) |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
(4.12) |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Обозначим |
rI m через |
|
Urm |
|
и |
L I m через ULm , |
тогда |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U rm |
, |
|
|
|
|
U Lm |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im |
|
|
|
|
|
I m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2r |
2xL |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
Разделив обе части этих выражений на |
|
2 ,перейдѐм к действующим |
||||||||||||||||||||||||||||||||||||||||
значениям: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
I |
|
U r |
|
|
I |
U L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
r |
, |
|
|
|
xL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.13) |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
На основании (4.11) построим векторную диаграмму. Алгебраическую |
||||||||||||||||||||||||||||||||||||||||||
мгновенных значений заменим геометрической суммой действующих значений: |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.14) |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
U Ur U L |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
Отложим в масштабе действующее значение тока в цепи I . |
Обход цепи |
|||||||||||||||||||||||||||||||||||||||||
начнем |
|
с |
активного |
|
сопротивления |
|
|
|
|
|
r . |
Падение |
напряжения |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
U r |
r I |
откладываем по направлению тока ( |
|
U r |
|
совпадает по направлению с |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
током) - рис.4.19. К вектору |
|
|
согласно (4.14) пристраиваем вектор U L |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
который как видно из(4.II) и (4.12), опережает ток на угол |
/2. Замыкающий |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
вектор |
|
U будет |
|
равен |
|
действующему |
|
напряжению |
на |
зажимах цепи. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
U |
|
|
|
U 2 |
U 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Диаграмму напряжений (рис.4.19) |
называют треугольником |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
a
Рис.4.19
напряжений, из которого очевидно, что действующее значение напряжения на зажимах
|
|
|
U |
U 2 |
U 2 |
|
|
(4.15) |
|||||
|
|
|
|
|
r |
|
l |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
Заменив в (4.15) напряжения U r и Ul |
произведением сопротивления на ток |
||||||||||||
I (4.13), получим |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
U r2 |
U L2 = I r 2 |
xL2 Iz |
(4.16) |
||||||
|
|
|
|
|
|
|
|||||||
где |
z |
- |
называется полным сопротивлением цепи: z |
|
r 2 xL2 Полное |
||||||||
сопротивление |
z |
можно представить |
в |
|
виде |
треугольника |
сопротивлений |
||||||
(рис.4.20), разделив стороны треугольника напряжений (рис.4.19) на величину тока I

|
|
49 |
|
|
|
|
I |
U |
|
|
U |
|
(4.18) |
|
|
|
|
|
||
z |
|
|
|
|
||
|
|
r 2 xL2 |
||||
|
|
|
|
|
||
Из (4.16) следует, что между током I и напряжением на зажимах U имеется сдвиг по фазе, равный углу 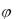 который определяется или из треугольника напряжений:
который определяется или из треугольника напряжений:
|
U l |
cos |
U r |
|
U L |
|
tg |
U |
sin |
||||
|
||||||
U r |
|
U |
||||
|
|
|
|
или из треугольника сопротивлений (4.20):
tg |
xL / r |
(4.19) |
cos |
r / z |
(4.20) |
|
|
|
sin |
x L / z |
(4.21) |
.20.
Из формул (4.19), (4.20), (4.21) и из рис.4.20 видна роль индуктивности в образовании угла и в увеличении общего сопротивления цепи для синусоидального переменного тока. Зная угол сдвига фазы напряжения по отношению к току, нетрудно написать мгновенное значение напряжения (4.II) для цепи с активно-индуктивным сопротивлением: для тока
|
|
|
|
i Im sin wt : |
U 2U sin(wt ) |
||
|
|
|
|
Умножив стороны треугольника напряжений (рис.4.19) на ток I получим треугольник мощностей (4.21), из которого видно, что гипотенуза треугольника является полной мощностью:
S zI 2 UI |
(4.22) |
Горизонтальный катет в том же масштабе равен активной мощности:
P rI 2 U I UI cos |
S cos |
(4.23) |
r |
|
|
|
|
другой катет равен реактивной мощности:
Q |
x |
L |
I 2 |
UI sin |
S sin |
(4.24) |
l |
|
|
|
|
|
Рис. 4.21.
Полную мощность S можно выразить иначе:
S= P 2 Q 2 |
(4.25) |

50
Размерность мощности: активной (Р)=Вт, реактивной (Q)=вар, полной (S)=ВА.
Как было принято ранее, активная, или полезная мощность определяется как среднее значение мощности за период. Поэтому мгновенное значение мощности Р можно определить как:
P |
1 |
T Uidt |
1 |
T U m sin( t )I m sin |
|
tdt |
UI cos |
|
(4.26) |
||
|
|
|
|||||||||
|
T 0 |
T 0 |
|
|
|
|
|
|
|
||
|
|
|
|
|
cos |
|
P |
|
|
|
|
В выражении |
(4.26) |
множитель |
|
|
|
- |
коэффициент мощности |
||||
|
S |
||||||||||
|
|
||||||||||
(безразмерная величина). |
|
|
|
|
|
|
|
|
|
||
Наличие в цепи индуктивности снижает коэффициент мощности и тем |
|||||||||||
уменьшает полезную мощность. Только при |
L |
=0, когда cos |
=1, вся мощность |
||||||||
источника S=UI превращается в полезную мощность |
Р |
, во всех других |
|||||||||
случаях при L 0 |
|
cos 1 и полезная мощность P<S. |
|
|
|||||||
4.9. Синусоидальный ток в цепи с емкостью
Вспомним основные свойства емкости, известные из физики. Емкость - это две металлические пластины, разделенные диэлектриком (рис.4.22). При постоянном токе металлические пластины, разделенные диэлектриком, представляют разрыв цепи и, следовательно, ток через емкость не проходит.
При переменном токе напряжение, приложенное к пластинам, непрерывно с частотой f меняет знак. При этом на пластинах с частотой f меняется знак электрических зарядов, что приводит к созданию непрерывно меняющегося по величине и направлению электрического поля между пластинами и появлению в цепи с емкостью переменного тока:
i dq / dt |
(4.27) |
Величина заряда q в любой момент времени пропорциональна значению емкости С и напряжению на пластинах:
|
q=CU |
|
(4.28) |
Таким образом: емкость С |
является |
своего рода |
коэффициентом |
пропорциональности между зарядом |
q |
и величиной |
приложенного |
напряжения U . Величина емкости зависит от расстояния между пластинами, от качества диэлектрика и размеров пластины. Ёмкость рассчитывается по формуле:
C |
0 S |
|
d |
||
|
