
- •18. Постоянный электрический ток.
- •19. Электрические токи в вакууме.
- •17. Вещество в электрическом поле.
- •16. Потенциал.
- •4. Диэлектрическая проницаемость среды.
- •15. Электростатика.
- •3.Электрическое поле и его напряженность.
- •9.Молекулярно – кинетические явления.
- •4.Скорость поступательного движения молекул газов.
- •10.Молекулярные столкновения, проникновения.
- •11. Явления передачи.
- •12. Основы термодинамики.
- •4.Работа , совершаемая при изменении объёма газа.
- •13. Адиабатический процесс.
- •1. Цикл Карно. Цикл Карно состоит из четырёх стадий:
- •14. Реальные газа, жидкости и твёрдые тела.
17. Вещество в электрическом поле.
1.
Явление электростатической индукции
в проводниках. В
1831г. Англ. Физик Фарадей открыл явление
электромагнитной индукции заключ. В
том что в замкнутом контуре L
при изменении потока
 магнитной индукции охватываемого эти
контурам возникает электрический ток,
получивший название индукционного.
Величина индукционного тока совершенно
не зависит от способа изменения потока
магнитной индукции, а определяется
лишь скоростью его изменения. Открытие
явления электромагнитной индукции
имело большое значение, так как была
доказана возможностью получения
электрического тока с помощью магнитного
поля. Этим была установлена взаимосвязь
между электрическими и магнитными
полями. Возникновение индукционного
тока указывает на наличие в явлении
электромагнитной индукции электродвижущей
силы, называемой электродвижущей
индукции. Обобщая результаты своих
многочисленных опытов. М. Фарадей пришёл
к количественному закону электромагнитной
индукции: величина индукции тока, а
следовательно, и ЭДС электромагнитной
индукции
магнитной индукции охватываемого эти
контурам возникает электрический ток,
получивший название индукционного.
Величина индукционного тока совершенно
не зависит от способа изменения потока
магнитной индукции, а определяется
лишь скоростью его изменения. Открытие
явления электромагнитной индукции
имело большое значение, так как была
доказана возможностью получения
электрического тока с помощью магнитного
поля. Этим была установлена взаимосвязь
между электрическими и магнитными
полями. Возникновение индукционного
тока указывает на наличие в явлении
электромагнитной индукции электродвижущей
силы, называемой электродвижущей
индукции. Обобщая результаты своих
многочисленных опытов. М. Фарадей пришёл
к количественному закону электромагнитной
индукции: величина индукции тока, а
следовательно, и ЭДС электромагнитной
индукции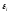 определяется только скоростью изменения
магнитного потока,
определяется только скоростью изменения
магнитного потока, -
Закон Фарадея.
-
Закон Фарадея.
С
учётам правила Ленца закон электромагнитной
индукции записывается в виде:
 -Закон
Фарадея-Ленца. Знак «минус« в формуле
(2) и является математическим выражением
правила Ленца, установленного в 1833 г.
Для нахождения направления индукционного
тока.
-Закон
Фарадея-Ленца. Знак «минус« в формуле
(2) и является математическим выражением
правила Ленца, установленного в 1833 г.
Для нахождения направления индукционного
тока.
2.
электроёмкость. Разные
проводники. Имеющие одинаковые заряды
 ,
приобретают различные потенциалы.
Поэтому для уединённого проводника
можно записатьg=C
,
приобретают различные потенциалы.
Поэтому для уединённого проводника
можно записатьg=C .
Величину C=g/
.
Величину C=g/ .
Называют электроёмкостью проводника.
Емкость проводника зависит только от
его размеров и формы. Это связано с тем,
что избыточные заряды распределяются
по внешней поверхности проводника.
Единица электроёмкости – фарад (Ф):
1Ф-емкость такого уединённого проводника,
потенциал которого изменяется на 1В
при сообщении ему заряда 1 Кл (1Ф=1 Кл/1В).
.
Называют электроёмкостью проводника.
Емкость проводника зависит только от
его размеров и формы. Это связано с тем,
что избыточные заряды распределяются
по внешней поверхности проводника.
Единица электроёмкости – фарад (Ф):
1Ф-емкость такого уединённого проводника,
потенциал которого изменяется на 1В
при сообщении ему заряда 1 Кл (1Ф=1 Кл/1В).
3.Конденсатор.
На практике,
однако, необходимы устройства, обладающие
достаточно большой емкостью. Такие
устройства получили название
конденсаторов. Простейший конденсатор
состоит из двух параллельных металлических
пластин-обкладок, разделённых тонким
слоем диэлектрика. Обкладки этого
конденсатора, называемого плоским,
сообщаются разноименные равные по
величине заряды. Под емкостью плоского
конденсатора понимается отношение
положительного заряда g,
накопленного на обкладке с потенциалом
 к разности потенциалов∆
к разности потенциалов∆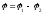 между его обкладками (
между его обкладками ( >
> :
: .
Если площадь каждой пластиныS,
расстояние между пластинами d
и пластины разделены диэлектриком с
диэлектрической проницаемостью ε, то
для емкости плоского конденсатора
получается выражение:
.
Если площадь каждой пластиныS,
расстояние между пластинами d
и пластины разделены диэлектриком с
диэлектрической проницаемостью ε, то
для емкости плоского конденсатора
получается выражение:
 .
.
При
параллельном соединении конденсаторов
суммарный заряд поэтому полная емкость
батареи равна сумме емкостей отдельных
конденсаторов:
 .
При последовательном соединении
конденсаторов напряжение батареи
.
При последовательном соединении
конденсаторов напряжение батареи ,
поэтому суммируются обратные величины
емкостей:
,
поэтому суммируются обратные величины
емкостей: ,
при последовательном соединении
конденсаторов результирующая емкость
С всегда меньше наименьшей емкости в
батарее конденсаторов.
,
при последовательном соединении
конденсаторов результирующая емкость
С всегда меньше наименьшей емкости в
батарее конденсаторов.
4.
Энергия электрического поля. Электрическая
энергия
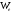 заряженного
проводника равна работе затраченной
на зарядку проводника,
заряженного
проводника равна работе затраченной
на зарядку проводника, .
Как всякий заряженный проводник,
конденсатор обладает электрической
энергией, которая может быть рассчитана
по формуле:
.
Как всякий заряженный проводник,
конденсатор обладает электрической
энергией, которая может быть рассчитана
по формуле: .
Если в эту формулу подставим электроёмкость
С плоского конденсатора , а разность
потенциалов∆
.
Если в эту формулу подставим электроёмкость
С плоского конденсатора , а разность
потенциалов∆ заменим
на произведении напряженности Е на
расстояниеd
между пластинами, то получим формулу:
заменим
на произведении напряженности Е на
расстояниеd
между пластинами, то получим формулу:
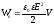 ,
где V=S*d
объем конденсатора.(15). Формула (15)
показывает что энергия конденсатора
а следовательно и его электрического
поля пропорциональна квадрату
напряжённости и объёму, в котором
существует однородное поле. Указанное
выражение соответствует представлениям
теории поля (теории близкодействия).
Считается что электрическая энергия
подобно ве-ву распределена в пространстве
с объемной плотностью
,
где V=S*d
объем конденсатора.(15). Формула (15)
показывает что энергия конденсатора
а следовательно и его электрического
поля пропорциональна квадрату
напряжённости и объёму, в котором
существует однородное поле. Указанное
выражение соответствует представлениям
теории поля (теории близкодействия).
Считается что электрическая энергия
подобно ве-ву распределена в пространстве
с объемной плотностью
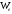 :
: ,
т.е. плотность энергии электрического
поля называется отношение его энергии
к объему, в котором это поле существует.
,
т.е. плотность энергии электрического
поля называется отношение его энергии
к объему, в котором это поле существует.
