
- •1.Кинематика материальной точки и твёрдого тела.
- •1. Связь физики с другими науками и производством.
- •2.Динамика материальной точки.
- •4.Механика твёрдого тела.
- •4.Основной закон динамики вращения.
- •6. Теорема об изменении момента импульса.
- •4. Гидростатическое уравнение.
- •6.Механические колебания.
- •3.Вынужденое колебание. Резонанс.
- •7.Волны.
1.Кинематика материальной точки и твёрдого тела.
1. Связь физики с другими науками и производством.
физика оказывает большое влияние на развитие производства. Достаточно напомнить, что физика дала производству электроэнергетику, все виды транспорта, радиосвязь, ядерную энергетику, телевидение. Уместно также отметить что процессы жизнедеятельности растений и леса в значительной мере определяются физическими условиями среды: световым, тепловым, водным и воздушными режимами. Задача физики состоит в изучении этих условий и установлении наиболее благоприятных режимов для их роста. Большое значение имеют изучение физических проблем фотосинтеза и исследования по воздействию на растения таких физических факторов, как ультразвуковые колебания, радиоактивные излучения различного рода.
2.Основные характеристики движения. Механическим движением тела называется изменение положения тела или его частей в пространстве относительно других тел с течением времени. Положенное тело в пространстве и его движение можно задать только относительно другого тела( тела отсчёта). Выбранное таким образом тело словно считается неподвижным, а связанная с ним система координат и часы для определения времени образуют систему отсчёта.
3. Общий случай криволинейного движения материальной точки.
Материальной точкой наз-т тело,размерами и внутр.структурой кот-го в конкретной задаче можно при небречь,а всю массу тела считать сконцентрированной в одной точке.Линию,которую описывает материальная точка при дв-ии в опред-ной с-ме отсчета,наз-ют траекторией движения.Вид траектории дв-я своб.матер.точки зависит от сил,кот-ые действуют на нее,нач.условий и с-мы отсчета,а вид траектории дв-я несвободной точки – от хар-ра связей.Прямолинейным дв-ем наз-ся дв-е, траекторией которого в данной системе отсчета явл-ся прямая линия.Криволинейным наз-ся дв-е,траекторией которого в данной задаче явл-ся некоторая кривая линия.
4.
Угловой
скоростью
называется векторная величина, равная
первой производной угла поворота тела
по времени:
![]() Вектор
направлен вдоль оси вращения по правилу
правого винта, т.е. так же, как и вектор
(рис.7). Размерность угловой скорости
dim w=T–1, а ее единица — радиан в секунду
(рад/с). Линейная скорость точки (см.
рис. 6)
Вектор
направлен вдоль оси вращения по правилу
правого винта, т.е. так же, как и вектор
(рис.7). Размерность угловой скорости
dim w=T–1, а ее единица — радиан в секунду
(рад/с). Линейная скорость точки (см.
рис. 6)![]() т.
е.
т.
е. В
векторном виде формулу для линейной
скорости можно написать как векторное
произведение:
В
векторном виде формулу для линейной
скорости можно написать как векторное
произведение:![]() При
этом модуль векторного произведения,
по определению, равен
При
этом модуль векторного произведения,
по определению, равен![]() ,
а направление совпадает с направлением
поступательного движения правого винта
при его вращении отωкR.Если
(ω= coмассаnst,
то вращение равномерное и его можно
характеризовать периодом
вращения T
— временем, за которое точка совершает
один полный оборот, т.е. поворачивается
на угол 2. Так как промежутку времени
t
= T
соответствует∆φ= 2, тоω =
2/T,
откуда
,
а направление совпадает с направлением
поступательного движения правого винта
при его вращении отωкR.Если
(ω= coмассаnst,
то вращение равномерное и его можно
характеризовать периодом
вращения T
— временем, за которое точка совершает
один полный оборот, т.е. поворачивается
на угол 2. Так как промежутку времени
t
= T
соответствует∆φ= 2, тоω =
2/T,
откуда![]() Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называется частотой
вращения:
Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называется частотой
вращения:![]()
![]() откуда
откуда![]() Угловым
ускорением называется векторная
величина, равная первой производной
угловой скорости по времени:
Угловым
ускорением называется векторная
величина, равная первой производной
угловой скорости по времени:![]() При
вращении тела вокруг неподвижной оси
вектор углового ускорения направлен
вдоль оси вращения в сторону вектора
элементарного приращения угловой
скорости. При ускоренном движении
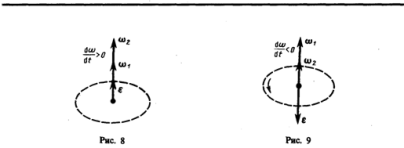
вектор ε сонаправлен векторуω(рис.8),
при замедленном — противонаправлен
ему (рис.9).Тангенциальная составляющая
ускорения
При
вращении тела вокруг неподвижной оси
вектор углового ускорения направлен
вдоль оси вращения в сторону вектора
элементарного приращения угловой
скорости. При ускоренном движении
вектор ε сонаправлен векторуω(рис.8),
при замедленном — противонаправлен
ему (рис.9).Тангенциальная составляющая
ускорения![]()
![]() Нормальная
составляющая ускорения
Нормальная
составляющая ускорения![]()
 Таким
образом, связь между линейными (длина
пути s, пройденного точкой по дуге
окружности радиуса R, линейная скорость
v, тангенциальное ускорениеα, нормальное
ускорениеα, ) и угловыми величинами
(угол поворота , угловая скорость ,
угловое ускорение ) выражается
следующими формулами:
Таким
образом, связь между линейными (длина
пути s, пройденного точкой по дуге
окружности радиуса R, линейная скорость
v, тангенциальное ускорениеα, нормальное
ускорениеα, ) и угловыми величинами
(угол поворота , угловая скорость ,
угловое ускорение ) выражается
следующими формулами:![]() В
случае равнопеременного движения точки
по окружности (=const)
В
случае равнопеременного движения точки
по окружности (=const)
![]() где
0
— начальная угловая скорость.
где
0
— начальная угловая скорость.
