Надійність та діагностика

Практическая работа №7

Расчет надежности восстанавливаемых систем, а также систем с использованием элементов математической логики

Цель: изучить и научиться рассчитывать в зависимости от исходных данных надежность восстанавливаемых систем, а также систем с использованием элементов математической логики.

Теоретический материал

РАСЧЕТ НАДЕЖНОСТИ С ИСПОЛЬЗОВАНИЕМ ЭЛЕМЕНТОВ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

Расчет надежности сложного объекта, по существу, является определением истинности сложного высказывания. Использование аппарата математического логики позволяет формализовать условия работоспособности сложных структур и получать формулы для расчета надежности.

1. Если о системе можно утверждать, что она работоспособна, если работоспособны ее элементы a и b, то можно сделать вывод о том, что работоспособность системы (событие с) и работоспособности элементов a и b (событие a и событие b) связаны между собой логическим уравнением работоспособности:

Логическое уравнение работоспособности для данного случая может бать представлено схемой последовательного соединения элементов a и b (рис. 7.1).

Рис. 7.1. Схема последовательного соединения элементов.

2. Если о системе можно утверждать, что она работоспособна, если работоспособны ее элемент a или элемент b, можно сделать вывод о том, что работоспособность системы (событие c) и работоспособности элементов a и b (событие a и событие b) связаны между собой логическим уравнением работоспособности:

Этому уравнению соответствует схема параллельного соединения элементов a и b (рис. 7.2).

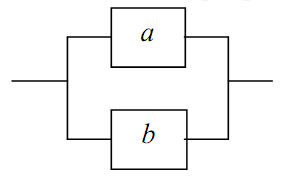
Рис. 7.2. Схема параллельного соединения элементов.

3. Если работоспособное состояние элемента обозначить через a , то неработоспособное состояние этого элемента будет a . Логическое отрицание может быть отражено в виде схемы инвертора (рис. 7.3).

Рис. 7.3. Схема инвертирования

4. Логические операции конъюнкции, дизъюнкции и отрицания - основные операции, используемые в теории надежности, так как к ним могут быть сведены все другие логические операции.

5. Сложную логическую функцию можно минимизировать, т.е. преобразовать таким образом, что она будет содержать минимальное число членов.

6. Логические функции можно преобразовать в алгебраические функции, если заменить все логические операции арифметическими по следующим правилам:

Логическая функция работоспособности F_Λ , у которой все логические операции заменены арифметическими, называется функцией работоспособности, представленной в арифметическом виде F_a .

Последовательность расчета надежности с использованием логических схем. Чтобы получить формулу для вероятности работоспособного состояния сложного объекта (функцию надежности), необходимо:

1. сформулировать словесно условие работоспособности системы;

2. на основании словесной формулировки записать логическую функцию работоспособности F_Λ ;

3. минимизировать F_Λ (исключить повторяющиеся члены);

4. в логической функции работоспособности заменить логические операции арифметическими, т.е. получить функцию F_a ;

5. в арифметической функции работоспособности заменить простые события (простые высказывания) их вероятностями;

6. в полученную формулу, дающую связь между вероятностями состояний элементов системы и вероятностью состояния системы, подставить числовые значения вероятностей состояний элементов. Решением полученного уравнения является численное значение вероятности работоспособного состояния сложной системы.

РАСЧЕТ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМЫХ СИСТЕМ

Как уже отмечалось ранее, в качестве показателей надежности восстанавливаемых объектов используются параметр потока отказов ω(t), вероятность безотказной работы в течение наработки (0,t)−P(t), коэффициент готовности K_Г(t), коэффициент вынужденного простоя системы K_П (t).

Нерезервированная система может находиться в произвольный момент времени t в одном из двух состояний: 0 - система работоспособна; 1 - система неработоспособна и находится в ремонте.

Если обозначить вероятности этих состояний через P₀(t) и P₁(t), то, очевидно, что K_Г(t) = P₀(t) и K_П(t) = P₁(t). При длительной эксплуатации (t → ∞) могут быть достигнуты установившиеся значения K_Г = P₀ и K_П = P₁ .

Если время безотказной работы и время восстановления имеют показательное распределение, то для вычисления функций готовности и простоя системы можно применить марковскую модель. Тогда в соответствии с графом состояний системы (рис. 7.4) имеем следующую систему дифференциальных уравнений:

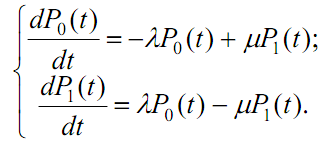(7.1)

Рис. 7.4. Граф состояний нерезервированной ремонтируемой системы: λ – интенсивность отказов; μ – интенсивность

Если при t = 0 система находилась в работоспособном состоянии, то начальные условия P₀(0)=1 , P₁(0)=0. Используя преобразования Лапласа, получим:

или

Решим систему по формулам Крамера:

Переходя от изображений к оригиналам (обратное преобразование Лапласа), получим:

(7.2)

(7.3)

Если при t=0 система находилась в ремонте, то P₀(0)=0 , P₁(0)=1 и результатом решения системы (7.1) будет:

При длительной эксплуатации получим стационарные значения коэффициентов готовности и простоя, не зависящие от начальных условий:

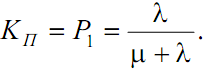
Поскольку

то приходим к уже известным выражениям:

т.е. коэффициент готовности характеризует долю времени, в течение которого система работоспособна, а коэффициент простоя - долю времени, в течение которого она восстанавливается (ремонтируется).

Если система имеет несколько работоспособных состояний, то функция готовности системы определяется как

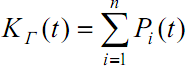
где n - число работоспособных состояний; P_i(t) - вероят-ность i-го работоспособного состояния.