Министерство образования и науки,

МОЛОДЕЖИ И СПОРТА УКРАИНЫ

ВОСТОЧНОУКРАИНСКИЙ НАЦИОНАЛЬНЫЙ УНИВЕРСИТЕТ

ИМЕНИ ВЛАДИМИРА ДАЛЯ

КАФЕДРА ПРИКЛАДНОЙ ФИЗИКИ

КУРСОВАЯ РАБОТА

по дисциплине «ЭВМ-эксперимент и машинная обработка информации»

ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ

Студент: Отрохов Е. А.

группа ПН-221

Преподаватель: доц. Калюжный Г.С.

Луганск, 2011

Аннотация

В данной работе будут рассмотрены три метода приближённого интегрирования определённого интеграла: метод прямоугольников, метод трапеций и метод Симпсона. Все эти методы будут подробно выведены с оценкой погрешности каждого из них. В работу включено наглядное применение нахождения определенного интеграла методом прямоугольников и трапеций. В материале имеются иллюстрации, с помощью которых, можно более глубоко вникнуть в суть рассматриваемой темы.

Оглавление

1. Введение 2

2. Математическая модель 3

2.2 Приближённые методы вычисления. 6

3. Исследование модели 22

3.1 Программа для вычисления интеграла 23

3.2 Определение значения интеграла с помощью метода прямоугольников. Сравнение результатов 25

4. Заключение 26

Список литературы 27

1. Введение

Основная цель этой работы заключается в ознакомлении с численным интегрированием. Суть численного интегрирования заключается в том, что подынтегральную функцию  заменяют другой приближенной функцией, так, чтобы, во-первых, она была близка к первоначальной функции и, во вторых, интеграл от нее легко вычислялся. Методы численного интегрирования, основаны на замене подынтегральной функции интерполяционным многочленом. Это позволяет приближенно заменить определенный интеграл интерполяционной суммой. В зависимости от способа ее вычисления получаются разные методы численного интегрирования, такие как:

• метод прямоугольников;

• метод трапеций;

• метод Симпсона.

В частности при выполнении данной работы использовался метод трапеций.

2. Математическая модель

2.1.1 Определение интеграла и его геометрический смысл

В начале узнаем, что такое определённый интеграл. Возможны два различных подхода к определению определённого интеграла.

Приращение 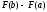любой из преобразованных функций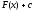при изменении аргумента от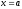до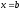называют определённым интегралом отa до b функции f и обозначается .

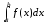Причём функция 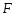является первообразной для функцииf на некотором промежутке D, а числа а и b принадлежат этому промежутку. Это можно записать следующим образом:

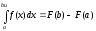(1)

это формула Ньютона-Лейбница.

Если при любой последовательности разбиений отрезка [a;b] таких, что 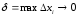(n→∞) и при любом выборе точек 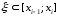интегральная сумма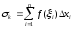стремится к одному и тому же конечному пределуА, то это число А и есть определённый интеграл, т.е.

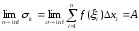(2)

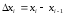
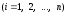
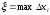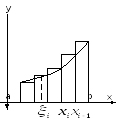
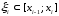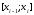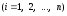Где – начало разбиения произвольная точка из отрезкасумма всех произведений . Простыми словами, определенный интеграл есть предел интегральной суммы, число членов которой неограниченно возрастает, а каждое слагаемое стремится к нулю.