3.1. Механизмы планирования

Распределение корпоративных заказов. Рассмотрим корпорацию, в которую входят n предприятий (Пр). Простейшая структура корпорации приведена на рисунке 3.1.

Органом управления корпорации является корпоративный центр (КЦ). В его функции входит установление корпоративных механизмов, разработка стратегии развития корпорации, распределение корпоративных заказов, распределение корпоративных финансов и т.д.

Рассмотрим задачу планирования – распределения корпоративных заказов. Пусть корпорация получила заказ на производство продукции в количестве R единиц по договорной цене С. Продукция может производиться на каждом предприятии (такое объединение предприятий называется горизонтальной интеграцией). Задача планирования заключается в распределении заказа между предприятиями, так чтобы прибыль корпорации была максимальной. Обозначим x_i – величину заказа, полученную i-ым предприятием, – функция производственных издержек z_i. Для исследования свойств механизмов управления во многих случаях конкретный вид функции производственных издержек не имеет большого значения. Поэтому возьмем ее в простейшем виде (см. также модель в разделе 5.4):

. (3.1)

где r_i - параметр, определяющий эффективность производства i-го предприятия. Эта функция удовлетворяет требованиям, обычно предъявляемым к функциям производственных издержек (возрастающая, выпуклая функция объемов производства). Прибыль (выигрыш, значение целевой функции) i-го предприятия составит:

, (3.2)

а суммарная прибыль корпорации:

, (3.3)

поскольку

. (3.4)

Так как договорная цена C и величина заказа R заданы, то задача максимизации прибыли корпорации сводится к задаче минимизации суммарных издержек:

(3.5)

при ограничении (3.4).

Оптимальное решение этой задачи:

(3.6)

где . То есть, заказ нужно распределять прямо пропорционально коэффициентам эффективности производства.

Проблема, однако, в том, что КЦ не знает точных значений {r_i}, а знает только область [d;D] возможных значений. Необходимо устранить эту неопределенность. Простейший способ - это запросить информацию о коэффициентах эффективности у предприятий (предполагаем, что предприятия знают точные оценки своих коэффициентов эффективности). Такой способ получения информации называется встречным. Обозначим оценку коэффициента r_i, сообщаемую i-ым предприятием в КЦ через s_i. Эта оценка используется в законе планирования (3.6), то есть:

(3.7)

где . Возникает вопрос, какую оценкуs_i сообщает каждое предприятие, максимизируя собственную прибыль:

. (3.8)

Определим план V_i , обеспечивающий максимальную прибыль предприятия (его легко найти, дифференцируя выражение (3.2)):

. (3.9)

Пусть , то есть сумма выгодных планов превышает величину заказа R. Если каждое предприятие сообщает истинную оценку s_i = r_i , то:

,

то есть каждое предприятие получает план меньше оптимального.

Естественно, что в этом случае возникает тенденция завышения сообщаемых оценок. Если CH>>R, то в ситуации равновесия Нэша каждое предприятие сообщает максимальную оценку s_i=D, что приводит к: x_i=R/n, то есть заказ делится поровну между всеми предприятиями. Прибыль корпорации при этом равна:

и может быть существенно меньше, чем прибыль Ф_max при оптимальном плане.

Пример 3.1. Пусть n=2, r₁=3, r₂=7, d=3, D=7, R=100, C=20. Ищем оптимальный план и прибыль: x₁⁰=30, x₂ ⁰=70, Ф_max = 1500.

В ситуации равновесия Нэша: s₁^*=s₂^*=7, x₁=x₂=50. Прибыль корпорации: , то есть потери составили примерно 7 %.

Как повысить эффективность планирования? Введем внутреннюю (корпоративную, трансфертную) цену продукции. Это цена, по которой КЦ как бы покупает продукцию у предприятий. Обозначим ее через . Внутренняя прибыль предприятия, равная

, (3.10)

достигает максимума при плане

. (3.11)

Выберем , так чтобы сумма выгодных (при цене ) планов равнялась величине заказа, то есть, из условия найдем .

Поскольку величина H корпоративному центру не известна, то возьмем вместо H сумму оценок S, то есть примем:

(3.12)

Заметим, что внутренняя прибыль это не реальные деньги, а некоторый управленческий показатель. Поэтому реально полученную прибыль будем распределять прямо пропорционально внутренним прибылям:

, (3.13)

где Ф₀ – реальная прибыль корпорации. Выражения (3.11)-(3.13) определяют новый механизм планирования, который отличается от прежнего введением внутренней цены и распределением реальной прибыли прямо пропорционально внутренним прибылям.

Для оценки эффективности этого механизма подставим (3.11) и (3.12) в (3.10), а затем в (3.13):

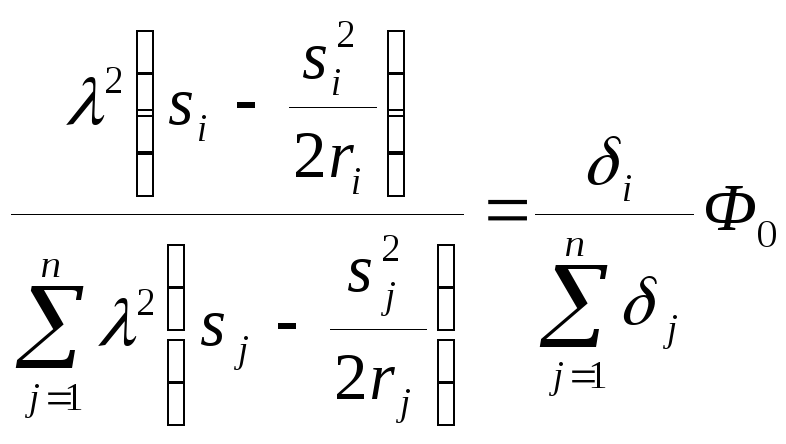, (3.14)

где .

Заметим, что (3.14) является возрастающей функцией . Поэтому максимум f_i достигается при максимуме . Максимум достигается при s_i=r_i, то есть при сообщении каждым предприятием достоверной оценки коэффициента эффективности. Таким образом, рассмотренный механизм является механизмом открытого управления (см. лекцию 5), то есть механизмом, в котором всем агентам выгодно сообщать достоверную информацию. Единственным недостатком механизма является перераспределение прибыли, которое может вызвать недовольство предприятий, у которых часть прибыли передают другим предприятиям. Однако в случае рассматриваемых функций производственных издержек никакого перераспределения прибыли не происходит. Действительно прибыль, полученная i-ым предприятием, равна . Прибыль, полученная после перераспределения, составит:

.

то есть, это – та же самая величина.

Подведем итоги. Предложенный механизм планирования имеет три замечательных свойства:

1. каждое предприятие сообщает достоверную информацию о функции производственных издержек. Другими словами, сообщение достоверной информации является доминантной стратегией каждого предприятия;

2. корпоративный центр определяет оптимальные планы распределения заказа;

3. перераспределение прибыли отсутствует.