Ранг матриці.

Оберемо в матриці А R рядків і R стовпців, де число R менше або дорівнює меншому з чисел m (число рядків матриці) та n (число стовпчиків матриці). Наприклад, якщо матриця розмірності , то R не перевищує 3. Якщо матриця , то R не перевищує 2. Визначник R-го порядку, складений з елементів, що стоять на перетині вибраних R рядків і R стовпців, називається визначником або мінором, породженим даною матрицею.

Рангом матриці називають найбільший порядок відмінних від нуля визначників (або мінорів), породжених даною матрицею.

Ранг матриці A зазвичай позначають або.

Якщо всі визначники R-го порядку, що породжені даною матрицею, дорівнюють нулю, то < R.

Властивості рангу матриці.

Ранг матриці не зміниться, якщо:

1. будь-які два рядки переставити місцями;

2. якщо всі елементи будь-якого рядку помножити на деяке постійне число, відмінне від нуля;

3. якщо до елементів будь-якого рядку додати елементи іншого рядку, помножених на постійне число.

Такі перетворення матриць називаються елементарними.

Матриці A і B називаються еквівалентними, якщо одна з них отримана шляхом елементарних перетворень іншої. Еквівалентність позначається: A~ B.

Базисним мінором матриці називають будь-який відмінний від нуля визначник або мінор, породжений даною матрицею, порядок якого дорівнює рангу r матриці.

Методи визначення рангу матриці.

1. Метод нулів і одиниць

За допомогою елементарних перетворень з матриці А може бути отримана матриця В, в якій всі стовпці (рядки) міститимуть або одні нулі, або нулі та лише одну одиницю. Ранг матриці А дорівнюватиме числу одиниць матриці В, оскільки A~ B.

2. Метод оздоблюючого мінору або визначників

Мінор порядку, що містить в собі всі елементи мінору, називають оздоблюючим мінором (або визначником) мінору.

Якщо усі мінори , породжені даною матрицею, дорівнюють нулю, та існує хоч би один мінор , то ранг матриці рівнийR .

Означення. Мінором елементу визначника -го порядку називається визначник (-1)-го порядку, отриманий з визначника (матриці) викреслюванням -го рядка і -го стовпця, на перетину яких знаходиться елемент.

Наприклад, у визначника існує мінор .

Обернена матриця

Нехай маємо квадратну матрицю порядку.

Матриця називаєтьсяоберненою до матриці , якщо має місце тотожність

,

де – одинична матриця, така, що

.

Квадратна матриця порядкуназиваєтьсяневиродженою (неособливою, регулярною), якщо її визначник відмінний від нуля (). У випадку, якщо визначник дорівнює нулю, матрицяназиваєтьсявиродженою.

Якщо матриця порядкує невиродженою, то для неї існує обернена матриця:

.

Приклад: Обчислити обернену матрицю для матриці

.

Оскільки , то матрицяне вироджена, тому для неї снує обернена матриця. Обчислимо алгебраїчні доповнення елементівматриціза формулою

.

;

;

;

;

;

;

;

;

.

Тоді

.

Зробимо перевірку обчислювань, перевіривши рівність

.

.

Таким чином, обчислення виконані вірно і тоді

.

Відповідь. .

Системи лінійних алгебраїчних рівнянь. Метод Крамера.

Нехай маємо систему лінійних алгебраїчних рівнянь, в якій число рівнянь дорівнює числу невідомих ().

Нехай дана система трьох рівнянь з трьома невідомими.

Запишемо головний визначник системи та побічні визначники,,:

, ,

, .

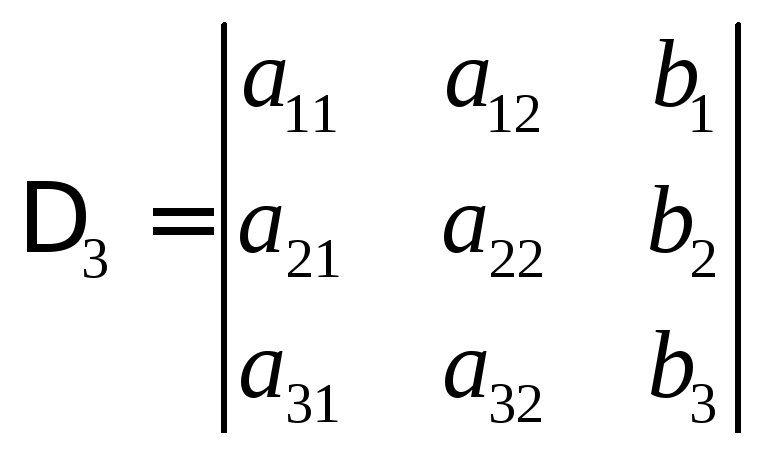Тоді ,,.

Якщо , то система має єдиний розв’язок.

Якщо , то система має нескінчену множину розв’язків. Але, якщо при цьому , то система розв’язків не має.

Прикладом цього є система рівнянь

Дослідимо цю систему пізніше за допомогою методу Гауса.

Якщо , а принаймні один(), то система не має розв’язків.

Однорідна система рівнянь має єдиний тривіальний розв’язок, коли , і нескінчену множину розв’язків, коли.

Приклад. Розв’язати систему рівнянь

. Значить система має єдиний розв’язок.

; ;.

Тоді

, ,.

Зробимо перевірку. Для цього в вихідну систему рівнянь підставимо знайдені значення змінних.

Відповідь. ,,.

Приклад: Знайти розв’язок системи рівнянь

.

, ,.

Система має нескінчену множину розв’язків. Одне з рівнянь є лінійною комбінацією двох інших рівнянь системи.

Нехай ,. Візьмемо тільки два перших рівняння:

,

, .

, ,,.

Відповідь. ,,.

Приклад: Знайти розв’язок системи

.

.

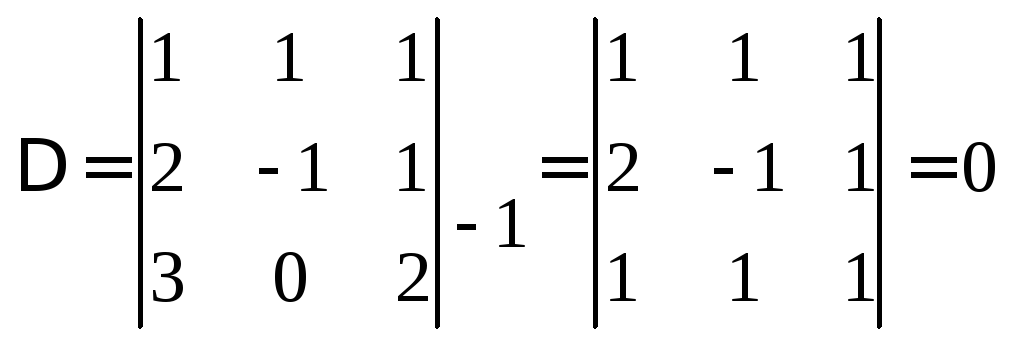
Відповідь. Система розв’язків не має.