2. Доказать тождество: .

3. Доказать, что и .

4. Даны множества и . Найти , , , , .

5. Доказать, что для всех выполняется утверждение:

.

6. Пусть А – множество прямых на плоскости и задано отношение R:. Какими свойствами обладает данное отношение?

7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. Множество А = {-10, -9, -8, -7, …, 0, 1, …9, 10} и (a, b) R, если a ³ = b ³.

8. Упростить выражение алгебры множеств: .

Вариант 17.

1. Известно, что из 60 студентов в секциях спортивного клуба занимаются: в гимнастической – 15, в волейбольной – 20, в баскетбольной – 25, в гимнастической и волейбольной – 5, в гимнастической и баскетбольной – 5, в волейбольной и баскетбольной – 10, во всех трех секциях – 3. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?

2. Доказать тождество: .

3. Доказать, что .

4. Даны множества и . Найти , , , , .

5. Доказать, что для всех натуральных выполняется утверждение:

.

6. На множестве действительных чисел задано отношение . Какими свойствами оно обладает?

7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. Множество А = {-10, -9, -8, -7, ..., 0, 1, …9, 10} и (a, b) R, если a ² = b ².

8. Упростить выражение алгебры множеств: .

Вариант 18.

1. Известно, что из 95 студентов в секциях спортивного клуба занимаются: в гимнастической – 25, в волейбольной – 40, в баскетбольной – 30, в гимнастической и волейбольной – 10, в гимнастической и баскетбольной – 8, в волейбольной и баскетбольной – 5, во всех трех секциях – 3. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?

2. Доказать тождество: .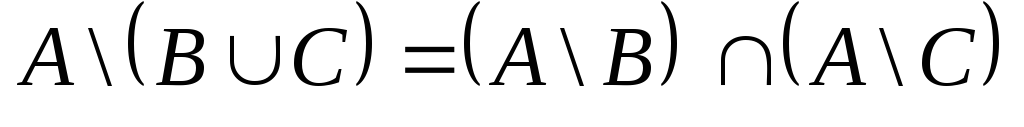

3. Доказать, что .

4. Даны множества и . Найти , , , , .

5. Доказать, что для всех выполняется утверждение:

.

6. На множестве задано отношение . Какими свойствами обладает данное отношение?

7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. А – множество упорядоченных пар целых чисел, и (a, b) R (c, d), если ad = bc.

8. Упростить выражение алгебры множеств: .

Вариант 19.

1. Известно, что из 100 студентов в секциях спортивного клуба занимаются: в гимнастической – 28, в волейбольной – 30, в баскетбольной – 42, в гимнастической и волейбольной – 8, в гимнастической и баскетбольной – 10, в волейбольной и баскетбольной – 5, во всех трех секциях – 3. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?

2. Доказать тождество: .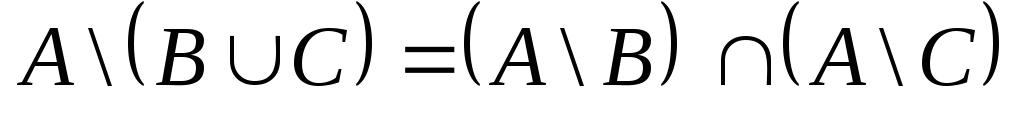

3. Доказать, что .

4. Даны множества и . Найти , , , , .

5. Доказать, что для всех выполняется утверждение:

.

6. Заданы два отношения R1 и R2, R1 – симметричное, рефлексивное, R2 – антисимметричное, антирефлексивное. Какими свойствами обладает отношение ?

7. Установите, является ли заданное отношение R на А отношением эквивалентности. Для каждого отношения эквивалентности постройте классы эквивалентности. {( x, y) | x, y A = Z и x + y = 5}.

8. Упростить выражение алгебры множеств: .

Вариант 20.

1. Известно, что из 75 студентов в секциях спортивного клуба занимаются: в гимнастической – 20, в волейбольной – 25, в баскетбольной – 30, в гимнастической и волейбольной – 7, в гимнастической и баскетбольной – 8, в волейбольной и баскетбольной – 6, во всех трех секциях – 4. Сколько студентов занимаются только в одной секции? Сколько не занимались ни в одной?