
Математика курс лекций 1 курс / Лекция 11. Функции одной переменной
.docxФункции одной переменной. Лекция 11.
Функции одной переменной.
Понятие функции.
Пусть
даны два непустых множества
 и
и
 .
Соответствие
.
Соответствие
 ,
которое каждому элементу
,
которое каждому элементу
 сопоставляет не более одного элемента
сопоставляет не более одного элемента
 называется функцией.
Так на рис. 43 отображение
называется функцией.
Так на рис. 43 отображение
 является функцией а на рис. 44 отображение
является функцией а на рис. 44 отображение
 не является функциональным, так как
один элемент множества
не является функциональным, так как
один элемент множества
 отображается на два элемента множества
отображается на два элемента множества
 .
В этом случае функция
.
В этом случае функция
 отображает множество
отображает множество
 на множество
на множество
 .
.

Множество
 называется областью
определения
функции
называется областью
определения
функции
 и обозначается
и обозначается
 .
Множество всех
.
Множество всех
 называется множеством
значений
функции
называется множеством
значений
функции
 и обозначается
и обозначается
 .
.
Если
 и
и
 числовые множества, то функция
числовые множества, то функция
 называется числовой
функцией.
Это записывается как
называется числовой
функцией.
Это записывается как
 .
В этом случае переменная
.
В этом случае переменная
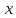 называется аргументом
или независимой
переменной,
а
называется аргументом
или независимой
переменной,
а
 – функцией
или зависимой
переменной.
Частное значение функции
– функцией
или зависимой
переменной.
Частное значение функции
 при
при
 записывается как
записывается как
 .
.
Так,
если
 ,
то
,
то
 ,
,

Графиком
функции
 называется множество всех точек плоскости
с координатами
называется множество всех точек плоскости
с координатами
 .
.
Способы задания функции.
Существуют различные способы отражения функциональной зависимости.
Аналитический: Функция определяется одной или несколькими формулами или в виде уравнений


Графический: В этом случае задается график функции (рис. 45).
Табличный. Функция задается таблицей ряда значений аргумента и соответствующих значений функции.
|
|
1 |
2 |
3 |
4 |
5 |
|
|
6 |
0 |
-2 |
5 |
4 |
Четные и нечетные функции.
Функция,
определенная на множестве
 ,
называется четной
(нечетной),
если для любого элемента
,
называется четной
(нечетной),
если для любого элемента
 выполняются следующие условия:
выполняются следующие условия:
1)

2)

График
четной функции симметричен относительно
оси
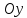 ,
а нечетной – относительно начала
координат точки
,
а нечетной – относительно начала
координат точки
 .
.
Четными
являются, например, функции:
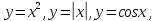

Нечетными
являются функции:


Функции
 не являются четными и не являются
нечетными. Они называются функциями
общего вида.
не являются четными и не являются
нечетными. Они называются функциями
общего вида.
Монотонные функции.
Пусть
функция
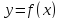 определена на множестве
определена на множестве
 и
и
 .
Если для любых значений
.
Если для любых значений
 :
:
1)
из неравенства
 следует
следует
 ,
то функция
,
то функция
 называется возрастающей (неубывающей)
на множестве
называется возрастающей (неубывающей)
на множестве
 ;
;
2)
из неравенства
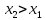 следует
следует
 ,
то функция
,
то функция
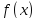 называется убывающей (невозрастающей)
на множестве
называется убывающей (невозрастающей)
на множестве
 .
.
Так
функция
 является возрастающей на всей числовой
оси
является возрастающей на всей числовой
оси
 а функция
а функция
 возрастает на интервале
возрастает на интервале
 и убывает на интервале
и убывает на интервале
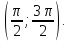
Возрастающие, неубывающие, убывающие и невозрастающие функции называются монотонными.
Ограниченные функции.
Функцию
 определенную на множестве
определенную на множестве
 ,
называют ограниченной на этом множестве,
если существует такое число
,
называют ограниченной на этом множестве,
если существует такое число
 ,
что для всех
,
что для всех
 выполняется
неравенство
выполняется
неравенство
 .
.
Так
функция
 ограничена на всей числовой оси (
ограничена на всей числовой оси ( ),
а функция
),
а функция
 ограничена на любом отрезке вида
ограничена на любом отрезке вида
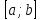 (интервале
(интервале
 )
(
)
( ).
).
Периодические функции.
Функция
 определенная на множестве
определенная на множестве
 ,
называется периодической
на этом множестве,
если существует такое наименьшее число
,
называется периодической
на этом множестве,
если существует такое наименьшее число
 ,
что при каждом
,
что при каждом
 выполняются условия
выполняются условия
 и
и
 .
При этом число
.
При этом число
 называется периодом
функции.
Периодами будут так же числа, кратные
называется периодом
функции.
Периодами будут так же числа, кратные
 т. е.
т. е.
 и т. д. Периодическими функциями являются
и т. д. Периодическими функциями являются
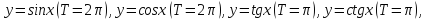
 .
.
Обратные функции.
Пусть
задана функция
 с областью определения
с областью определения
 и областью значений
и областью значений
 .
Если каждому
.
Если каждому
 соответствует единственное значение
соответствует единственное значение
 ,
такое, что
,
такое, что
 ,
то можно определить функцию
,
то можно определить функцию
 с областью определения
с областью определения
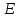 и областью значений
и областью значений
 ,
для которой из того, что
,
для которой из того, что
 следует равенство
следует равенство
 .
Такая функция называется обратной к
.
Такая функция называется обратной к
 и записывается как
и записывается как
 .
Так как независимая переменная
обозначается через
.
Так как независимая переменная
обозначается через
 ,
а зависимая через
,
а зависимая через
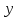 ,
то обратную функцию записывают так же
в виде
,
то обратную функцию записывают так же
в виде
 Приведем примеры функций и их обратных.
Приведем примеры функций и их обратных.
Для
 обратная функция так же
обратная функция так же
 ,
для
,
для
 обратной будет функция
обратной будет функция
 ,
для
,
для
 обратной будет
обратной будет
 ,
для показательной функции
,
для показательной функции
 обратной является логарифмическая
функция
обратной является логарифмическая
функция
 ,
для функции
,
для функции
 на
отрезке
на
отрезке
 обратной будет
обратной будет
 .
.
В
общем случае, для построения обратной
функции к функции
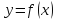 переменные
переменные
 и
и
 в записи функции меняют местами и
выражают снова переменную
в записи функции меняют местами и
выражают снова переменную
 .
.
Основные свойства обратных функций.
1)
Если задана функция
 и ее обратная
и ее обратная
 ,
то справедливы соотношения
,
то справедливы соотношения


2) если исходная функция возрастает (убывает), то и обратная функция так же возрастает (убывает);
3) графики взаимно обратных функций симметричны относительно биссектрисы 1-го и 3-го координатных углов (рис. 46);
4) всякая монотонная функция имеет обратную функцию.
Сложная функция.
Пусть
функция
 определена на множестве
определена на множестве
 ,
а функция
,
а функция
 определена на множестве
определена на множестве
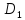 .
Тогда на множестве
.
Тогда на множестве
 определена функция
определена функция
 ,
которая называется сложной
функцией
от
,
которая называется сложной
функцией
от
 или суперпозицией
функций
или суперпозицией
функций
 и
и
 .
Примерами сложных функций являются
функции
.
Примерами сложных функций являются
функции
 .
.
Основные элементарные функции и их графики.
На рисунках изображены эскизы графиков основных элементарных функций.
Степенные функции.
1)
 ,
,
 (рис. 47 а);
(рис. 47 а);
2)
 (рис. 47 б);
(рис. 47 б);
3)
 ,
,
 (рис 47 в);
(рис 47 в);
4)
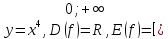 (рис. 47 г);
(рис. 47 г);
5)
 (рис. 47 д);
(рис. 47 д);
6)
 (рис. 47 е).
(рис. 47 е).
Показательные функции.
1)
 (рис. 48 а);
(рис. 48 а);
2)
 (рис. 48 б).
(рис. 48 б).
Логарифмические
функции.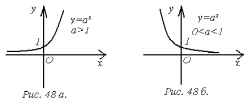
1)
 (рис. 49 а);
(рис. 49 а);
1)
 (рис. 49 б).
(рис. 49 б).
Тригонометрические функции.
1)
 (рис. 50 а);
(рис. 50 а);
2)
 (рис. 50 б);
(рис. 50 б);

3)
 (рис. 50 в);
(рис. 50 в);

4)
 (рис. 50 г);
(рис. 50 г);
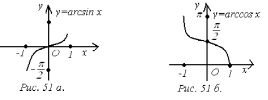
Обратные тригонометрические функции.
1)
 (рис. 51 а);
(рис. 51 а);
2)
 (рис. 51 б);
(рис. 51 б);
3)
 (рис. 52 а);
(рис. 52 а);
4)
 (рис. 52 б).
(рис. 52 б).
Функция
 возрастает, а функция
возрастает, а функция
 убывает на всей числовой оси.
убывает на всей числовой оси.



