
Математика курс лекций 1 курс / Лекция 15. Правила Лопиталя
.docxПравила Лопиталя. Лекция 15.
Формула Тэйлора.
Пусть
дана функция
 ,
определенная в некоторой окрестности
точки
,
определенная в некоторой окрестности
точки
 и имеющая в ней производную до
и имеющая в ней производную до
 порядка включительно. Для любого
порядка включительно. Для любого
 из этой окрестности представим функцию
в виде суммы степеней
из этой окрестности представим функцию
в виде суммы степеней
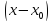 ,
т. е.
,
т. е.

Найдем
коэффициенты
 .
Для этого в равенстве
.
Для этого в равенстве
 положим
положим
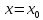 .
Тогда
.
Тогда
 .
Продифференцируем исходное равенство
.
Продифференцируем исходное равенство
 .
.
Приравняем
опять
 ,
получим
,
получим
 .
Продолжая этот процесс дальше, найдем
.
Продолжая этот процесс дальше, найдем
 ,
,
 ,
…,
,
…,
 .
Таким образом,
.
Таким образом,

Окончательно
выражение для
 примет вид
примет вид

Можно показать, что

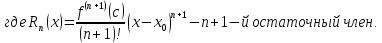
Точка
 находится между
находится между
 и
и
 ,
т. е.
,
т. е.
 .
Это равенство называется формулой
Тэйлора.
При
.
Это равенство называется формулой
Тэйлора.
При
 ,
получим
,
получим
 и формула совпадет с формулой Лагранжа.
и формула совпадет с формулой Лагранжа.
Пример
56.
Разложить функцию
 по степеням
по степеням
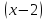 .
.
Решение.
По формуле Тэйлора для
 имеем
имеем
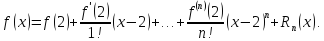
Найдем
производные и их значения в точке






Пятая
и все последующие производные будут
равны нулю, поэтому
 и получаем разложение
и получаем разложение


Если
в формуле Тэйлора положить
 получим частный случай - формулу Маклорена
получим частный случай - формулу Маклорена

где
 .
.
С помощью формулы Маклорена можно находить приближенные значения трансцендентных функций, разложение которых известно


где
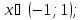



где

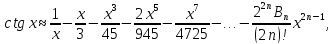
где
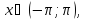
 – числа Бернулли
– числа Бернулли





Правила Лопиталя.
Теорема
30.
Пусть
функции
 и
и
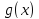 непрерывны и дифференцируемы в окрестности
точки
непрерывны и дифференцируемы в окрестности
точки
 и
и
 .
Если
.
Если
 в окрестности точки
в окрестности точки
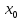 ,
то
,
то
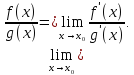
Доказательство.
Применим к функциям
 и
и
 теорему
Коши для отрезка
теорему
Коши для отрезка
 ,
лежащего в окрестности точки
,
лежащего в окрестности точки
 .
Тогда
.
Тогда

где
 .
Учитывая, что
.
Учитывая, что
 ,
получаем
,
получаем

При
 ,
величина
,
величина
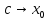 ,
тогда
,
тогда


Замечание
1. Теорема
верна и в случае, когда
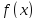 и
и
 не определены в точке
не определены в точке
 ,
но выполняется условие
,
но выполняется условие
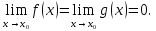
Замечание
2.
Теорема верна и для случая, когда
 .
Действительно, положим
.
Действительно, положим
 получим
получим
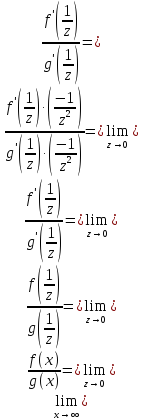
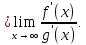
Теорема
31
(Без доказательства). Если
функции
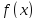 и
и
 непрерывны и дифференцируемы в окрестности
точки
непрерывны и дифференцируемы в окрестности
точки
 ( кроме может быть, самой точки
( кроме может быть, самой точки
 )
и в этой окрестности
)
и в этой окрестности
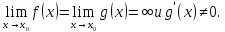
Если
существует предел

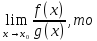

Пример 57. Вычислить предел
 используя
правила Лопиталя.
используя
правила Лопиталя.
Решение.

Пример 58. Вычислить предел
 используя
правила Лопиталя.
используя
правила Лопиталя.
Решение.
Предел имеет неопределенность вида
 ,
поэтому
,
поэтому
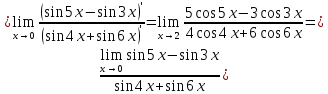

Пример 59. Вычислить предел
 используя
правила Лопиталя.
используя
правила Лопиталя.
Решение.
Обозначим искомый предел через
 и найдем
и найдем


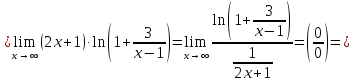



Таким
образом,
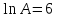 ,
отсюда
,
отсюда

