
Математика курс лекций 1 курс / Лекция 12. Пределы
.docxПределы. Лекция 12.
Пределы.
Окрестностью
произвольной точки
 будем считать любой интервал
будем считать любой интервал
 ,
содержащий эту точку.
,
содержащий эту точку.
Пусть
функция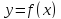 определена
в некоторой окрестности точки
определена
в некоторой окрестности точки
 ,
кроме, может быть, самой точки
,
кроме, может быть, самой точки
 .
.
Число
 называется пределом
функции
называется пределом
функции
 в точке
в точке
 ,
если для любого положительного числа
,
если для любого положительного числа
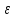 найдется такое положительное число
найдется такое положительное число
 ,
что для всех
,
что для всех
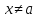 ,
удовлетворяющих условию
,
удовлетворяющих условию
 выполняется условие
выполняется условие
 .
В таком случае записывают
.
В таком случае записывают


Определение
предела в математических терминах можно
записать следующим образом (рис. 53):
Число
 называется пределом
функции
называется пределом
функции
 в точке
в точке
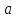 ,
если
,
если
 что
из условия
что
из условия
 следует
следует
 .
.
В
определении предела функции
 считается, что
считается, что
 стремится к
стремится к
 любым способом, оставаясь либо меньшим
любым способом, оставаясь либо меньшим
 ,
либо большим, либо колебаясь около точки
,
либо большим, либо колебаясь около точки
 .
.
Число
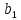 называется пределом
функции
называется пределом
функции
 слева в точке
слева в точке
 ,
если
,
если
если
 что
из условия
что
из условия
 следует
следует
 .
.
Записывается это как

Аналогично
определяется предел справа. Число
 называется пределом
функции
называется пределом
функции
 справа в точке
справа в точке
 ,
если если
,
если если
 что
из условия
что
из условия
 следует
следует
 .
Записывается это как
.
Записывается это как

Если
 ,
то предел функции
,
то предел функции
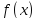 в точке
в точке
 не существует.
не существует.
Предел
функции при

Пусть
функция
 определена на всей числовой оси
определена на всей числовой оси
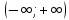 .
.
Число
 называется пределом
функции
называется пределом
функции
 при
при
 , если
, если
 ,
существует такое число
,
существует такое число
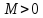 ,
что для всех
,
что для всех
 ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
 ,
выполняется неравенство
,
выполняется неравенство
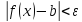 .
Записывается это как
.
Записывается это как
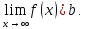
Бесконечно малые и бесконечно большие функции.
Функция
 называется бесконечно
большой при
называется бесконечно
большой при
 ,
если для любого числа
,
если для любого числа
 ,
,
 ,
что для всех
,
что для всех
 ,
удовлетворяющих неравенству
,
удовлетворяющих неравенству
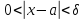 ,
выполняется неравенство
,
выполняется неравенство
 .
Записывается это как
.
Записывается это как
 при
при
 или
или

Если
при
 ,
,
 ,
то
,
то

Если
при
 ,
,
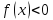 ,
то
,
то

Функция
 называется бесконечно малой при
называется бесконечно малой при
 ,
если
,
если

Свойства бесконечно малых функций.
1. Сумма бесконечно малых функций есть бесконечно малая функция.
2. Произведение ограниченной функции на бесконечно малую функцию есть бесконечно малая функция.
3. Произведение двух бесконечно малых функций есть бесконечно малая функция.
4. Частное от деления бесконечно малой функции на функцию, имеющую отличный от нуля предел, есть функция бесконечно малая.
5.
Если функция
 бесконечно малая, то функция
бесконечно малая, то функция
 есть бесконечно большая функция и
наоборот: если функция
есть бесконечно большая функция и
наоборот: если функция
 бесконечно большая, то
бесконечно большая, то
 есть бесконечно малая функция.
есть бесконечно малая функция.
Теоремы о связи предела функции и бесконечно малых.
Теорема
8. Если
функция
 имеет предел, равный
имеет предел, равный
 при
при
 ,
то ее можно представить как сумму числа
,
то ее можно представить как сумму числа
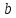 и бесконечно малой функции
и бесконечно малой функции
 ,
т. е. если
,
т. е. если
 то
то
 .
.
Доказательство.
Пусть
 тогда
тогда
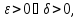 что
из условия
что
из условия
 следует
следует
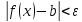 ,
т. е.
,
т. е.
 Следовательно
Следовательно

т.
е. функция
 является бесконечно малой при
является бесконечно малой при
 .
Отсюда
.
Отсюда
 .
Теорема доказана.
.
Теорема доказана.
Теорема
9
(обратная). Если
функцию
 можно представить в виде суммы числа
можно представить в виде суммы числа
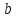 и бесконечно малой функции
и бесконечно малой функции
 ,
то
,
то
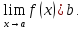
Доказательство.
Пусть
 ,
,
 .
Тогда
.
Тогда
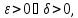 что
из условия
что
из условия
 следует
следует
 .
.
Так
как
 ,
то получим условие:
,
то получим условие:
 такое,
что из
такое,
что из
 следует
следует
 .
Следовательно,
.
Следовательно,

Основные теоремы о пределах.
Теорема 10. Предел суммы (разности) двух функций равен сумме (разности) их пределов. Т. е.
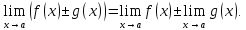
Доказательство. Пусть

Тогда
по теореме 7
 ,
,
 Следовательно,
Следовательно,
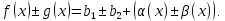
Так
как по свойству 1 бесконечно малых,
функция
 является бесконечно малой, то по теореме
8
является бесконечно малой, то по теореме
8

Теорема
11.
Функция
 может иметь только один предел при
может иметь только один предел при

Доказательство. Пусть

По теореме 9

Следовательно,
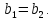
Теорема 12. Предел произведения двух функций равен произведению их пределов, т. е.

Доказательство.
Пусть

Тогда
по теореме 7
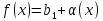 ,
,
 Следовательно,
Следовательно,

Так
как по свойствам 1- 3 бесконечно малых
функций, функция
 является бесконечно малой, то по теореме
8
является бесконечно малой, то по теореме
8

Теорема 13. Постоянный множитель можно выносить за знак предела.

Доказательство. По теореме 11

Теорема 14. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя неравен нулю. Т. е.

Доказательство.
Пусть

Тогда
по теореме 7,
 ,
,
 Следовательно,
Следовательно,


Так как по свойствам 1- 3 бесконечно малых функций, функция

является бесконечно малой, то по теореме 8

Непрерывность функций.
Пусть
функция
 определена в точке
определена в точке
 и в некоторой окрестности этой точки.
Функция
и в некоторой окрестности этой точки.
Функция
 называется непрерывной
в точке
называется непрерывной
в точке
 ,
если существует предел функции в этой
точке и он равен значению функции в этой
точке, т. е.
,
если существует предел функции в этой
точке и он равен значению функции в этой
точке, т. е.

Это
означает, что вычисление предела функции
в точке
 сводится к вычислению значения функции
сводится к вычислению значения функции
 в точке
в точке
 .
.
Точки, в которых нарушается непрерывность функции, называются точками разрыва этой функции.
Если
 точка разрыва функции
точка разрыва функции
 ,
то в ней не выполняется одно из следующих
условий:
,
то в ней не выполняется одно из следующих
условий:
1)
Функция определена в окрестности точки
 ,
но не определена в самой точке (рис. 54);
,
но не определена в самой точке (рис. 54);
2)
функция определена в точке
 и ее окрестности, но не существует
предела при
и ее окрестности, но не существует
предела при
 .
Например, функция
.
Например, функция 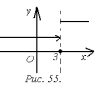
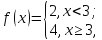
график которой изображен на рис. 55.
3)
функция определена в точке
 и ее окрестности, существует
и ее окрестности, существует
 но этот предел не равен значению
но этот предел не равен значению
 в точке
в точке
 (рис. 56).
(рис. 56).
Все точки разрыва функции разделяются на точки разрыва первого и второго рода.
Точка
разрыва
 называется точкой
разрыва первого рода,
если в этой точке существуют пределы
слева и справа, но они не равны
называется точкой
разрыва первого рода,
если в этой точке существуют пределы
слева и справа, но они не равны

Этому условию соответствуют точки, указанные на рисунках 55 и 56.
Точка
разрыва
 называется точкой
разрыва второго рода,
если, по крайней мере, один из односторонних
пределов равен плюс или минус бесконечности
(рис. 54).
называется точкой
разрыва второго рода,
если, по крайней мере, один из односторонних
пределов равен плюс или минус бесконечности
(рис. 54).
Примеры вычисления пределов.
Пример 36. Вычислить

Решение.
Так как функция
 определена в точке
определена в точке
 ,
то ее предел равен значению в этой точке
,
то ее предел равен значению в этой точке

Пример 37. Вычислить
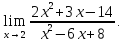
Решение.
Так как значения числителя и знаменателя
в точке
 равны нулю, то предел имеет неопределенность
вида
равны нулю, то предел имеет неопределенность
вида
 .
Преобразуем числитель и знаменатель,
воспользовавшись их разложением на
множители
.
Преобразуем числитель и знаменатель,
воспользовавшись их разложением на
множители

Таким
образом,
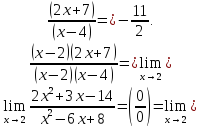
Пример
38.
Вычислить

Решение.
Так как значения числителя и знаменателя
в точке
 равны нулю, то предел имеет неопределенность
вида
равны нулю, то предел имеет неопределенность
вида
 .
Преобразуем дробь, домножив числитель
и знаменатель на сопряженное выражение
.
Преобразуем дробь, домножив числитель
и знаменатель на сопряженное выражение
 получим
получим

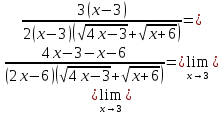

Признаки существования пределов.
Не
всякая функция имеет предел. Так функции
 и
и
 при
при
 не имеют пределов.
не имеют пределов.
Теорема
15.
Если
функция
 заключена между двумя функциями
заключена между двумя функциями
 и
и
 ,
стремящихся к одному и тому же пределу,
то он так же стремится к этому пределу,
т. е. если
,
стремящихся к одному и тому же пределу,
то он так же стремится к этому пределу,
т. е. если
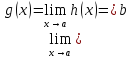
и
 ,
то
,
то
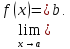
Доказательство. По определению предела


Тогда
для
 выполняются оба неравенства и
выполняются оба неравенства и

Так
как
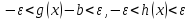 ,
то
,
то
 или
или

Теорема
16.
(Без доказательства). Если
функция
 является монотонной и ограниченной при
является монотонной и ограниченной при
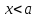 или при
или при
 ,
то существует ее левый предел
,
то существует ее левый предел
 или
ее правый предел
или
ее правый предел


Первый замечательный предел.
Теорема
17.


Доказательство.
Выберем на координатной плоскости круг
с единичным радиусом и центром в начале
координат (рис. 57). Построим в первой
четверти угол в
 радиан. Тогда длина дуги
радиан. Тогда длина дуги
 будет так же равна
будет так же равна
 .
Так как по построению
.
Так как по построению 
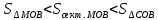
и
отрезки
 ,
то справедливы неравенства
,
то справедливы неравенства

Отсюда
разделив на
 ,
получим
,
получим


Так
как

то
по теореме 14, для
 имеем
имеем

Если
же
 ,
то
,
то
 и поэтому
и поэтому

Так как пределы слева и справа равны, то получаем окончательно

Замечание. Верным является так же и предел

Данный предел называют первым замечательным пределом.
Пример
39.
Вычислить
предел
 Решение. По свойству пределов
Решение. По свойству пределов

Пример
40.
Вычислить
предел
 Решение. По свойству пределов
Решение. По свойству пределов

Второй замечательный предел.
Теорема
18.
(Без доказательства).

где
 .
.
Так
как выражение в скобках стремится к
единице, то предел имеет неопределенность
 и называется вторым
замечательным пределом.
и называется вторым
замечательным пределом.
Пример 41. Вычислить
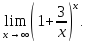
Решение.
Так как предел имеет неопределенность
вида
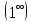 и, следовательно, является вторым
замечательным пределом, то
и, следовательно, является вторым
замечательным пределом, то

Пример 42. Вычислить

Решение.
Так как предел имеет неопределенность
вида
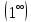 и, следовательно, является вторым
замечательным пределом, то
и, следовательно, является вторым
замечательным пределом, то


