
pechat_33
.pdf1.Классификация линейных уравнений в частных производных второго порядка в точке (в области). Особенности классификации в случае …
2.Приведение к каноническому виду линейных уравнений II-го порядка в случае 2-ух независимых переменных. Канонический вид уравнений …
3.Приведение к каноническому виду линейных уравнений II-го порядка в случае n независимых переменных.
4.*Постановка задачи Коши. Теорема Ковалевской.
5.Корректность постановки задачи. Примеры некорректно поставленных задач для ур-й гиперболического и параболического типа. Пример Адамара.
6.Задача Коши для одномерного волнового уравнения. Формула Даламбера. Выражение формулы Даламбера через среднее на отрезке.
7.*Осреднение функции на сфере и трехмерное волновое уравнение.
8.Задача Коши для трехмерного волнового уравнения. Формула Кирхгофа.
9.Задача Коши для двумерного вол-го ур-я. Метод спуска. Фор-а Пуассона.
10.Единственность и устойчивость решения задачи Коши для волнового уравнения.
11.*Элементарное (фундаментальное) решение уравнения теплопроводности.
12.Задача Коши для уравнения теплопроводности. Формула Пуассона.
13.Принцип экстремума для уравнения теплопроводности.
14.Единственность и устойчивость решения задачи Коши для уравнения теплопроводности.
15.Постановка смешанных задач для уравнений параболического и гиперболического типа.
16.*Формулы Грина. Формулы Грина для оператора Лапласа. 17.*Самосопряженность дифференциального оператора. 18.Задача Штурма-Лиувилля. Свойства собственных значений и собственных функций.
19.Метод Фурье решения смешанных задач для однородных уравнений гиперболического и параболического типа.
20.Реш-е смешанных задач для неоднородных уравнений гиперболического и параболического типа. Задачи с неоднородными граничными условиями. 21.Распределение температуры в прямоугольной области. 22.*Уравнения Бесселя. Функции Бесселя. 23.Радиальные колебания круглой мембраны.
24.Единственность решений смешанных задач для волновых уравнений и уравнений теплопроводности.
25.Ур-я эллиптического типа. Фундаментальное реш-е урав-я Лапласа. Связь аналитической фун-и комплексного переменного и гармонической … 26.*Интегральное представление произвольной и гармонической
функций (Интегральная теорема Гаусса).
27.Свойства гармонических функций: аналитичность, теорема о среднем на сфере.
28.Принцип максимума-минимума для гармонических функций.
29.Задачи Дирихле и Неймана для уравнения Пуассона. 30.Решение задачи Дирихле для уравнения Лапласа в круге и вне круга методом разделения переменных. Формула Пуассона. 31.Внутренняя и внешняя задача Неймана для круга. Необходимое условие существования решения. Теорема Гаусса.
32.Функции Грина задач Дирихле и Неймана.
33.Формула Пуассона решения задачи Дирихле для шара.
34.Формула Пуассона решения задачи Дирихле для круга.
35.Неравенство Харнака. Теорема Лиувилля
36.Уравнение колебаний струны.
37.Уравнение колебания мембраны.
38.*Уравнение колебаний электромагнитного поля.
39.Уравнение теплопроводности.
40.Объемный потенциал. Потенциал простого слоя. Потенциал двойного слоя.
41.*Свойства объемного потенциала.
42.*Свойства потенциала простого слоя.
43.Свойства потенциала двойного слоя.
44.*Использование потенциалов для решения задач Дирихле и Неймана
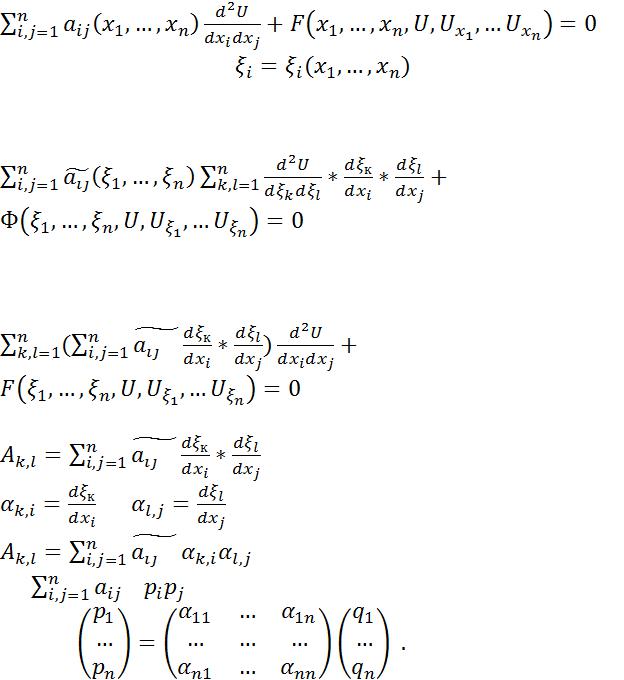
1.Классификация уравнений в частных производных в точке (в области). Особенности классификации в случае двух независимых переменных.Будем изучать лин. ур-ния в частных производных 2-го порядка.Любое ур-ние может быть записано в виде
(1
).В (1) сделаем замену: |
,при этом |
 ,затем после подстановки в ур-ние (1) получим
,затем после подстановки в ур-ние (1) получим
Если зафиксируем точку ( )то последнее ур-ние можно переписать в виде
)то последнее ур-ние можно переписать в виде
-квадратичная форма.Если
,а то
|
Рассмотрим квадратичную форму |
Q= |
и сделаем |
замену: |
Отсюда и получен |
способ классификации.Из алгебры известно,что любая кВ.ю форма может быть приведена к виду: Q= ,где
,где
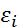 принимает значения 1,0 и -1.
принимает значения 1,0 и -1.
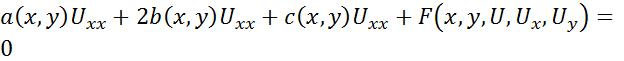
Ур-ние типа 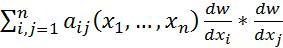 наз ур-нием
наз ур-нием
характеристик.
Если 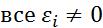 имеют одинаковый знак, то уравнения относятся к уравнениям эллиптического типа. Если все
имеют одинаковый знак, то уравнения относятся к уравнениям эллиптического типа. Если все
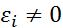 и n-1 из них имеет одинаковый знак, а оставшийся одинпротивоположный, то тип уравнения гиперболический. Если среди
и n-1 из них имеет одинаковый знак, а оставшийся одинпротивоположный, то тип уравнения гиперболический. Если среди 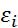 один равен 0, оставшиеся n- 1 имеют один знак, то уравнения параболического типа. Рассм.ур-ние 2-го порядка в случае двух переменных:
один равен 0, оставшиеся n- 1 имеют один знак, то уравнения параболического типа. Рассм.ур-ние 2-го порядка в случае двух переменных:
.Составим квадратичную формулу:
Q=a(x,y)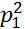 +2b(x,y)p1p2+c(x,y)
+2b(x,y)p1p2+c(x,y)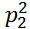 =a[
=a[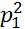 +2
+2 p1p2 +
p1p2 + 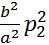 -
-
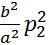 +
+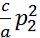 ]=a[
]=a[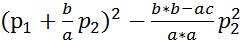 ].Обозначим δ=b*b-ac
].Обозначим δ=b*b-ac
и назовем его дискриминантом. Если δ<0,то ур-ние эллиптического типа. Если δ=0 то параболического и если δ>0 то гиперболического типа.
2.Приведение к каноническому виду уравнения 2 – го порядка в случае 2 – х независимых переменных. Канонический вид
уравнений гиперболического, параболического и эллиптического типа.
Рассмотрим уравнение
a(x, y)U xx 2b(x, y)U xy c(x, y)U yy F(x, y,U ,U x ,U y ) 0 |
. (1) |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выясним закон преобразования этого уравнения путем |
|
||||||||||||||||||||||||||||||||||
замены (x, y), (x, y) (2) |
при |
y 0. После применения |
|||||||||||||||||||||||||||||||||
(2) мы перейдем к уравнению |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
( , )U 2 ( , )U ( , )U ( , ,U,U |
,U ) 0. |
(3) |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выразим производные по x, y через производные по , . |
|
||||||||||||||||||||||||||||||||||
U x U x U x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
U y U y U y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
U |
xx |
U |
|
( |
x |
)2 2U |
|
|
x |
|
x |
U |
|
( |
x |
)2 |
U |
|
|
xx |
U |
|
|
|
xx |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
U |
yy |
U |
|
( |
y |
)2 2U |
|
( |
y |
) U |
|
( |
y |
)2 |
U |
|
|
yy |
U |
|
|
yy |
|
||||||||||||
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
U xy U ( x y ) U ( x y y x ) U ( x y ) U xy U xy .
Подставим найденные значения производных в уравнение
(1) и выпишем коэффициенты при вторых производных по
, .
|
|
2 |
2b( x y ) c( y ) |
2 |
|
|
|
|
|||||
a( x ) |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
x |
y ) c( y y ) |
|
||||||
a( x x ) b( x y |
|
||||||||||||
|
|
|
2b( ) c( )2 |
|
|
|
|
||||||
a( )2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
(4) |
|
|
x |
|
|
x y |
|
y |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
a |
|
2b |
|
|
c |
|
0. |
|||
Уравнение x |
|
|
|
|
|
|
|
|
|
||||
|
x |
|
|
y |
|
|
y |
(5) называется |
|||||
уравнением характеристик для уравнения (1) . |
|||||||||||||
|
' 2 ( x y x y )2 (b2 |
ac) y2 . Предположим, |
|||||||||||
что уравнение (1) мы рассматриваем в области, где 0.

Положим в (4) |
0 |
a( |
)2 2b( |
) c( |
)2 |
0 |
- |
|
|
x |
x y |
|
y |
|
|
||
уравнение характеристик. Коэффициент a |
в |
|
|
|
||||
рассматриваемой области отличен от нуля, если же a 0 , то считаем, что c 0.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
b b2 ac |
y |
(a 0). |
|
y |
|
b b2 ac |
|
x (c 0). |
||||||||||||||
|
|
a |
|
|
|
|
|
|
|
c |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
dy |
|
|
|
|
|
|
|
|||
a x (b ) y 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
b |
|
|
|
|
ady b |
|
dx |
|||||||||||||
|
|
|
(5) a |
|
|
|
||||||||||||||||||
Пусть (x, y) c1 , (x, y) c2 |
- общие интегралы последних |
|||||||||||||||||||||||
двух уравнений. |
U |
U ( , ,U ,U ,U ) 0. Рассмотрим |
||||||||||||||||||||||
случай, когда 0- уравнение параболического типа. каноническому виду уравнения параболического типа
U ( , ,U ,U ,U ) 0.
Рассмотрим теперь случай 0. Тогда уравнение характеристик примет вид:
a x (b i
 ) y 0 ady (b i
) y 0 ady (b i
 dx.) канонический вид уравнения эллиптического типа Уравнение гиперболического типа:
dx.) канонический вид уравнения эллиптического типа Уравнение гиперболического типа:
U U ( , ,U ,U ,U ) 0.
3.Приведение к каноническому виду уравнений второго порядка с постоянными коэффициентами в случае n
независимых переменных.
Рассмотрим уравнение второго порядка
n |
2u |
|
|
|
|
|
|
|
aij |
|
F(x1 |
,..., xn ,U ,U x |
,...,U x |
|
) |
(1), в котором |
|
xi y j |
n |
|||||||
i, j 1 |
|
1 |
|
|
||||
|
|
|
|
|
|
коэффициенты aij - постоянны. Соответствующая этому
n
уравнению квадратичная форма имеет вид: Q aij pi p j .
i 1
Эта квадратичная форма с помощью замены переменных p Aq при соответствующем выборе не особой матрицы A
|
|
|
n |
приводится к каноническому виду Qk k qk2 , ( k { 1,0,1}). |
|||
|
|
|
k 1 |
Уравнение (1) с помощью замены Ax может быть |
|||
приведено к виду |
|||
n |
2 |
|
|
k |
|
u |
( 1 ,..., n ,U ,U 1 ,...,U n ) 0.Установим связь |
|
2 |
||
k 1 |
k |
||
между матрицами A и B . Рассмотрим уравнение с двумя переменными. aU xx 2bU xy cU yy F1 (x, y,U ,U x ,U y ) 0 (2), в котором коэффициенты a, b, c постоянные, соответствующая этому уравнению квадратичная форма
Q ap12 |
2bp1 p2 |
cp22 . Сделаем замену p Bq |
|
|
|
|||||||||||||
p1 |
|
b11 |
b12 |
q1 |
|
b11q1 |
b12 q2 |
|
Q |
* |
a(b11q1 |
b12 q2 ) |
2 |
2b(b11q1 |
b12 q2 ) |
|||
|
|
|
|
b |
|
|
|
|
b q |
|
|
|
|
|||||
p |
2 |
|
b |
q |
2 |
|
b q |
2 |
|
|
|
|
|
|
|
|
||
|
|
21 |
22 |
|
|
21 1 |
22 |
|
|
|
|
|
|
|
|
|||
(b21q1 b22 q2 ) c(b21q1 b22 q2 )2 q12 (ab112 2b11b21 cb212 ) 2q1q2 (ab11b12 b(b11b22
b12b21 ) cb21b22 ) q22 (ab122 2bb12b22 cb222 ).
В уравнении (1) сделаем замену:
|
|
a11 |
|
|
|
|
|
|
|
a21 |
|
a12 |
x |
a11 x a12 y |
|
||
|
|
|
|
, |
тогда |
|
|
|
|
|
|
a22 y |
a21 x a22 y |
|
|||
a(a11 )2 2ba11a12 c(a12 )2
aa11a21 b(a11a22 a21a12 ) ca12 a22
a(a21 )2 2ba21a22 c(a22 )2
a11 b11 , a12 b21 , a21 b12 , a22 b22 . То есть, A BT .
4.*Постановка задачи Коши. Теорема Ковалевской
Будем рассматривать линейное урние 2-го порядка. Любое линейное ур-ние можно записать в
виде:L[n]= |
|
|
(1) |
. В пространстве |
зададим незамкнутую |
без самопересечений поверхность Γ ур-нием g(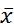 )=0. Причем будем считать что ф-ция g является дважды
)=0. Причем будем считать что ф-ция g является дважды
непрерывно дифференцируемой: g( |
и считаем |
|
такие, что grad |
: grad g( )=( |
).Обозначим |
через часть поверхности Γ, лежащей в области |
||
D,т.е. |
. |
|
Будем предполагать, что область D с поверхностью Γ разбиваеться на две подобласти D(1) и D(2).На поверхности 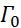 зададим два условия на неизвестную функцию U(x) удовлетворяющую уравнению
зададим два условия на неизвестную функцию U(x) удовлетворяющую уравнению
1: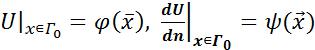 (2).Функции
(2).Функции 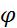 и
и 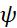
считаються замкнутыми ,n-единичная длина поверхности.Условие 2 наз.начальными условиями. Таким образом требуется найти функцию U 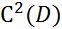 ,которая удовлетворяет ур-нию 1 в области D и начальным условиям 1 на поверхности
,которая удовлетворяет ур-нию 1 в области D и начальным условиям 1 на поверхности 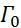 .В частности, если поверхность Γ являеться плоскость ,то начальное условие принимает вид:
.В частности, если поверхность Γ являеться плоскость ,то начальное условие принимает вид:
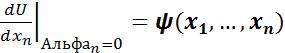 Функция удовлетворяющая
Функция удовлетворяющая
уравнению 1 и начальным условиям 2 наз.классическим решением задачи Коши. Отметим что не для всех функций  и
и такое решение
такое решение
существует: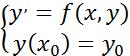 ,f(x,y)=
,f(x,y)=
то существует решение y= |
|
если f(x,y) |
||
аналитическая. |
|
|
|
|
Теорема Ковалевской. |
|
|
|
|
Если коэффициенты |
, |
,с, |
являются фун-ми |
|
аналитическими, как фун-и переменных |
, а |
|||
начальные функции |
и |
также аналитические по |
|
|
переменным |
то |
фиксированной точки |
|
|
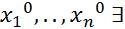 некоторая окрестность, в которой решение задачи 1 и 2
некоторая окрестность, в которой решение задачи 1 и 2 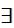 и ! в классе аналитических функций.
и ! в классе аналитических функций.

5. Корректность постановки задачи. Примеры некорректно поставленных задач для уравнений гиперболического и параболического типа. Пример Адамара.
Задача считается корректно поставленной, если:1)решение этой задачи существует;2)решение должно быть единственным;3)решение должно быть устойчиво. Приведем пример задачи, не корректно поставленной.
y ' 0 |
y c1 x c2 |
y c1 x 1 |
- не корректно |
|
|
1 |
y(0) 1 1 c2 1 |
|
|
y(0) |
y 2x 1 |
|
||
поставленная задача Приведем пример задачи, в которой нарушается
устойчивость решений (пример Адамара). Рассмотрим задачу :
U |
tt |
U |
xx |
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
(x).,где (x) и (x) - некоторые |
|||
U |
|
t 0 |
(x),U |
t |
t 0 |
|||||||
|
|
|
|
|
|
|
|
|
|
|||
известные функции. Пусть U1 (x,t) - решение задачи. |
||||||||||||
Рассмотрим еще одну задачу: |
|
|||||||||||
U U |
|
0 |
|
|
|
|
|
|||||
|
tt |
|
|
|
xx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
t 0 (x) |
1 |
cos nx,Ut t 0 (x). |
Пусть U2 (x,t) - решение |
|||||||
U |
|
|
|
|||||||||
|
n |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
этого уравнения. Составим разность U2 (x,t) U1 (x,t) V (x,t), тогда V (x,t) - решение задачи
V V |
xx |
0 |
|
|
1 |
|
|
||
|
|
|
|
|
|
|
|
||
tt |
|
|
|
|
|
|
|
|
|
|
t 0 |
1 |
|
0. |
U 2 (x, t) U1 (x, t) |
|
cos nx, |
при n . |
|
|
|
||||||||
V |
|
cos nx,Vt t 0 |
|
n |
|
|
|||
n |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
U 2t (x,t) U1t (x,t) 0. |
Найдем решение задачи для функции V в |
|||||
виде V T (t) cos nx. |
|
|
|
|
||
|
2 |
|
|
|
|
|
T (t) cos nx n T cos nx 0 |
|
|
|
|||
|
2 |
|
1 |
|
T (0). |
|
(T |
n T ) cos nx 0 |
V t 0 T (0) cos nx T (0) |
|
, Vt t 0 |
||
n |
||||||
T n T 0 |
|
|
|
|||
|
2 |
|
|
|
||
