Понятие метрического пространства

1. Определение и основные примеры. Одной из важнейших операций анализа является предельный переход. В основе этой операции лежит тот факт, что на числовой прямой определено расстояние от одной точки до другой. Многие фундаментальные факты анализа не связаны с алгебраической природой действи­тельных чисел (т. е. с тем, что они образуют поле), а опираются лишь на понятие расстояния. Обобщая представление о действи­тельных числах как о множестве, в котором введено расстояние между элементами, мы приходим к понятию метрического пространства — одному из важнейших понятий современной математики. Ниже мы изложим основные факты теории метри­ческих пространств и их обобщения — топологических про­странств. Результаты этой главы существенны для всего даль­нейшего изложения.

Определение. Метрическим пространством называется пара (X, р), состоящая из некоторого множества (пространства) X элементов (точек) и расстояния, т. е. однозначной, неотрица* тельной, действительной функции р(х; у), определенной для лю­бых х и у из X и подчиненной следующим трем аксиомам:

1. р (x, y) = 0 тогда и только тогда, когда х = у,

2. р(x, y)= р(у, x) (аксиома симметрии),

3. р(x,z) ≤ р(x, y) + р(у,z) (аксиома треугольника).

Само метрическое пространство, т. е. пару (X, р), мы будем обозначать, как правило, одной буквой:

R = (X, р).

В случаях, когда недоразумения исключены, мы будем за­частую обозначать метрическое пространство тем же символом, что и сам «запас точек» X.

Примеры метрических пространств

Приведем примеры метрических пространств. Некоторые из этих пространств играют в анализе весьма важную роль.

1. Положив для элементов произвольного множества

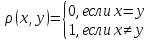
мы получим, очевидно, метрическое пространство. Его можно назвать пространством изолированных точек.

2. Множество действительных чисел с расстоянием

|

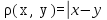образует метрическое пространство R¹.

3. Множество упорядоченных групп из n действительных чисел x=(x₁,x₂,…x_n) с расстоянием

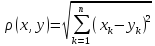(1)

называется n-мерным арифметическим евклидовым пространством Rⁿ. Справедливость аксиомы 1) и 2)для Rⁿ очевидна. Покажем что, в Rⁿ выполнена и аксиома треугольника.

Пусть x=(x_1,… ,x_n), y=(y₁,… y_n) и z=(z_1,… z_n);

тогда аксиома треугольника записывается в виде

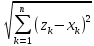≤ + (2)

Полагая y_k – x_k = a_k, z_k – y_k= b_k, получаем z_k – x_k = a_k + b_k,

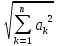≤+ (3)

Но это неравенство сразу следует из известного неравенства Коши-Бурянковского

≤ (4)

Действительно в силу этого неравенства имеем

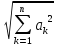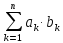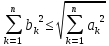=+2++2+=

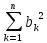Тем самым неравенство (3), а следовательно и (2), доказано. 4. Рассмотрим то же самое множество упорядоченных групп из п действительных чисел х = (х_х,… ,х_п), ио расстояние опре­делим в нем формулой

(5)

Справедливость аксиом 1)—3) здесь очевидна. Обозначим это метрическое пространство символом Rⁿ.

Возьмем снова то же самое множество, что и в приме­рах 3 и 4, и определим расстояние между его элементами формулой

(6)

Справедливость аксиом 1)—3) очевидна. Это пространство, ко­торое мы рбозначим 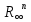, во многих вопросах анализа не менее удобно, чем евклидово пространство Rⁿ.

Последние три примера показывают, что иногда и в самом деле важно иметь различные обозначения для самого метриче­ского пространства и для множества его точек, так как один и; тот же запас точек может быть по-разному метризован.

Множество С [а, b] всех непрерывных действительных функ­ций, определенных на сегменте [a, b], с расстоянием

(7)

также образует метрическое пространство. Аксиомы 1)—3) про­веряются непосредственно. Это пространство играет очень важ­ную роль в анализе. Мы будем его обозначать тем же симво­лом С [а, b], что и само множество точек этого пространства. Вместо С[0, 1] мы будем писать просто С.