
- •1.Множества. Операции над множествами
- •2.Бинарные отношения, их типы. Примеры
- •3.Перестановки с повторениями и без.
- •4.Сочетания с повторениями и без.
- •5.Высказывания. Операции над высказываниями.
- •6.Булевы функции. Теорема о числе булевых функций.
- •7.Формулы алгебры логики и их классификация, примеры
- •8.Законы равносильности.
- •9.Днф и кнф
- •10.Алгебра Жегалкина. Полином Жегалкина
- •11.Теоремы о разложении.
- •12.Сднф и скнф. Алгоритмы их нахождения.
- •13.Контактные и логические схемы.
- •14.Сокращенная днф и алгоритмы ее построения.
- •15.Минимальная днф. Метод импликации матриц.
- •16.Тупиковые днф
- •17.Полнота и замкнутость
- •18.Важнейшие замкнутые классы.
- •19.Алгоритм Поста.
- •20.Предикаты. Область истинности, теорема об области истинности
- •21.Операции над предикатами.
- •22.Формулы алгебры логики предикатов и их классификация
- •23.Законы Де Моргана
- •24.Закон пронесения квантора общности через конъюнкцию
- •25.Закон пронесения квантора существования через дизъюнкцию
- •26.Детерминированные функции от одной переменной
- •27.Детерминированные функции от двух переменных
- •28.Машина Тьюринга
- •29.Примитивно рекурсивные функции. Примеры
- •30. Рекурсивные функции. Примеры
30. Рекурсивные функции. Примеры
Определение 2 Функция f называется частично рекурсивной функцией, если она может быть получена из простейших функций с помощью операции суперпозиции, примитивной рекурсии и минимизации, взятых конечное число раз в любой последовательности.
Класс частично рекурсивных функций обозначим Prp.
Обозначим через Pp– класс рекурсивных функций, т.е. всех числовых функций из Prp.
Пример
9 Доказать, что частично числовая функция
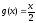 частично рекурсивна.
частично рекурсивна.
Вначале
заметим, что данная функция получается
из функции
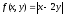 с
помощью операции минимизации, т.е.
с
помощью операции минимизации, т.е.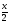 =
My
=
My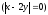 .
.
Согласно
примерам 2 и 4 функция
 примитивно рекурсивна. А это значит,
что
примитивно рекурсивна. А это значит,
что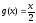 –
частично рекурсивная функция.
–
частично рекурсивная функция.
Данный пример показывает, что класс Prp существенно шире, чем класс Pp. Можно сказать, что и класс Pp существенно шире, чем класс Pnp, т.е.
Pnp С Pp С Prp.
