
- •1.Множества. Операции над множествами
- •2.Бинарные отношения, их типы. Примеры
- •3.Перестановки с повторениями и без.
- •4.Сочетания с повторениями и без.
- •5.Высказывания. Операции над высказываниями.
- •6.Булевы функции. Теорема о числе булевых функций.
- •7.Формулы алгебры логики и их классификация, примеры
- •8.Законы равносильности.
- •9.Днф и кнф
- •10.Алгебра Жегалкина. Полином Жегалкина
- •11.Теоремы о разложении.
- •12.Сднф и скнф. Алгоритмы их нахождения.
- •13.Контактные и логические схемы.
- •14.Сокращенная днф и алгоритмы ее построения.
- •15.Минимальная днф. Метод импликации матриц.
- •16.Тупиковые днф
- •17.Полнота и замкнутость
- •18.Важнейшие замкнутые классы.
- •19.Алгоритм Поста.
- •20.Предикаты. Область истинности, теорема об области истинности
- •21.Операции над предикатами.
- •22.Формулы алгебры логики предикатов и их классификация
- •23.Законы Де Моргана
- •24.Закон пронесения квантора общности через конъюнкцию
- •25.Закон пронесения квантора существования через дизъюнкцию
- •26.Детерминированные функции от одной переменной
- •27.Детерминированные функции от двух переменных
- •28.Машина Тьюринга
- •29.Примитивно рекурсивные функции. Примеры
- •30. Рекурсивные функции. Примеры
9.Днф и кнф
1)ДНФ назыв. дизъюнкция элементар. коньюкций
2)КНФ назыв. коньюкция элементар. дизъюнкций
Формула
вида
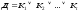 (краткая запись
(краткая запись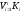 ),
где
),
где – конъюнкции
– конъюнкции называется дизъюнктивной нормальной
формой (ДНФ). Для любой формулы алгебры
логики существует равносильная ей
дизъюнктивная нормальная форма.
называется дизъюнктивной нормальной
формой (ДНФ). Для любой формулы алгебры
логики существует равносильная ей
дизъюнктивная нормальная форма.
Форма
вида 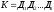 (краткая запись
(краткая запись ),
где
),
где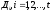 - дизъюнкции
- дизъюнкции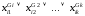 называется конъюнктивной нормальной
формой (КНФ).
называется конъюнктивной нормальной
формой (КНФ).
Такими являются, например, выражения:
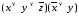 ,
,
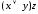 .
Для любой формулы алгебры логики
существует равносильная ей конъюнктивная
нормальная форма.
.
Для любой формулы алгебры логики
существует равносильная ей конъюнктивная
нормальная форма.
10.Алгебра Жегалкина. Полином Жегалкина
Множество булевых функций, рассматриваемое вместе с операциями конъюнкции и сложения (по модулю два), будем называть алгеброй Жегалкина.
Непосредственно проверкой (с помощью таблиц истинности) устанавливаются следующие законы:
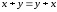 – закон
коммутативности;
– закон
коммутативности;
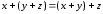 – закон ассоциативности;
– закон ассоциативности;
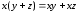 – закон
дистрибутивности;
– закон
дистрибутивности;
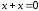 ;
;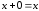 .
.
В алгебре Жегалкина роль совершенных нормальных форм булевой алгебры играют полиномы Жегалкина.
Полиномом
Жегалкина называется полином вида
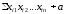
причем
в каждом наборе
 все координаты различны, а суммирование
ведется по некоторому множеству таких
не совпадающих наборов, а – константа
0 или 1.
все координаты различны, а суммирование
ведется по некоторому множеству таких
не совпадающих наборов, а – константа
0 или 1.
Например,
выражение
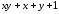 является полиномом Жегалкина, а выражения
является полиномом Жегалкина, а выражения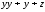 и
и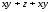 – нет, так как в первом выражении имеется
конъюнкция, содержащая две переменные
y, а второе выражение содержит два
одинаковых слагаемых
– нет, так как в первом выражении имеется
конъюнкция, содержащая две переменные
y, а второе выражение содержит два
одинаковых слагаемых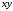 и
и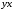 .
.
Каждая булева функция может быть единственным образом выражена при помощи полинома Жегалкина.
11.Теоремы о разложении.
1 Всякая булева функция f(x1,x2,…,xn) может быть представлена в следующей форме:
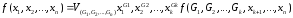 ,
,
где 1 ≤ k ≤ n, в дизъюнкции берется по всем наборам значений переменных.
Разложение по переменной Xn:
 (3.2)
(3.2)
Если булева функция не есть константа 0, то справедливо разложение
Разложение по всем переменным:
 ,
,
 (3.3)
(3.3)
где дизъюнкция
берется по всем наборам
 ,
при которых значение функции
,
при которых значение функции равно 1.
равно 1.
Теорема 2
Всякая булева функция
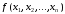 может быть представлена в следующей
форме:
может быть представлена в следующей
форме:
 (3.4)
(3.4)
где 1≤k≤n, а конъюнкция берется по всем 2k наборам значений переменных.
Теорема3.Для любой формулы алгебры логики существует равносильная ей дизъюнктивная нормальная форма.
Теорема 4 Для любой формулы алгебры логики существует равносильная ей конъюнктивная нормальная форма.
Теорема 4 Формула алгебры логики тогда и только тогда является тождественно истинной, когда каждая дизъюнкция в ее конъюнктивной нормальной форме содержит некоторую переменную вместе с ее отрицанием.
Теорема 5 Формула алгебры логики тогда и только тогда является тождественно ложной, когда каждая конъюнкция в ее дизъюнктивной форме содержит некоторую переменную вместе с ее отрицанием.
12.Сднф и скнф. Алгоритмы их нахождения.
 ,
,

называется совершенной дизъюнктивной нормальной формой (сокращенная запись СДНФ) функции.
Разложение
(3.3) дает способ построения СДНФ. Для
этого в таблице истинности отмечаем
все строки
 ,
в которых
,
в которых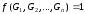 .
Для каждой такой строки образуем
конъюнкцию
.
Для каждой такой строки образуем
конъюнкцию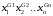 и затем все полученные конъюнкции
соединяем знаком дизъюнкции.
и затем все полученные конъюнкции
соединяем знаком дизъюнкции.
Таким
образом, существует взаимно однозначное
соответствие между таблицей истинности
функции
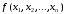 и ее СДНФ. А это значит, что СДНФ для
булевой функции единственна.
и ее СДНФ. А это значит, что СДНФ для
булевой функции единственна.
Единая булева функция, не имеющая СДНФ, есть константа 0.
 ,
,

разложение
носит название совершенной конъюнктивной
нормальной формы (СКНФ). Разложение
(3.6) дает способ построения СКНФ. Для
этого в таблице истинности отмечаем
все строки
 ,
в которых
,
в которых .
Для каждой такой строки образуем
дизъюнкцию
.
Для каждой такой строки образуем
дизъюнкцию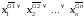 и затем все полученные конъюнкции
соединяем знаком конъюнкции. Таким
образом, существует взаимно
и затем все полученные конъюнкции
соединяем знаком конъюнкции. Таким
образом, существует взаимно
однозначное
соответствие между таблицей истинности
функции
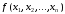 и ее СКНФ. А это значит, что СКНФ для
булевой функции единственна.
и ее СКНФ. А это значит, что СКНФ для
булевой функции единственна.
Единственная булева функция, не имеющая СКНФ, есть константа 1
