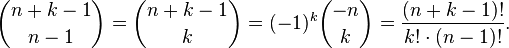1.Множества. Операции над множествами

Множеством называется совокупность некоторых элементов, объединенных каким-либо общим признаком. Элементами множества могут быть числа, фигуры, предметы, понятия и т.п. Множества обозначаются прописными буквами, а элементы множество строчными буквами. Элементы множеств заключаются в фигурные скобки.

Если элемент x принадлежит множеству X, то записывают x ∈ Х (∈ — принадлежит). Если множество А является частью множества В, то записывают А ⊂ В (⊂ — содержится).

Основные числовые множества N,Z,Q,R,C

Операции

Два множества А и В равны (А=В), если они состоят из одних и тех же элементов.

Объединением (суммой) множеств А и В называется множество А ∪ В, элементы которого принадлежат хотя бы одному из этих множеств.

Пересечением (произведением) множеств А и В называется множество А ∩ В, элементы которого принадлежат как множеству А, так и множеству В. Разностью множеств А и В называется множество АВ, элементы которого принадлежат множесву А, но не принадлежат множеству В.

Симметричной разностью множеств А и В называется множество А Δ В, являющееся объединением разностей множеств АВ и ВА, то есть А Δ В = (АВ) ∪ (ВА).

2.Бинарные отношения, их типы. Примеры

Бинарным отношениеммежду множествами A и B называется любое подмножество p прямого произведения A x B. Часто чтобы обозначить принадлежность упорядоченной пары (x,y) к бинарному отношению p вместо записи (x,y)∈p используют обозначения p(x,y) или xpy. При этом говорят, что x находится в отношении p к y.Если A=B, то говорят, что p задано на множестве A.

Типы: 1)бинар. отнош. R между элементами множ. A назыв рефлексивным ɏa∈ A(a,a) ∈ R;

2) бинар. отнош. R назыв симметричным (a,b) ∈ R=>(b,a) ∈ R

3) бинар. отнош. R назыв транзитивным :(a,b) ∈ R,(b,c) ∈ R=>(a,c) ∈ R

Пример Пусть A={a,b,c,d,e,f,g,h}и B={1,2,3,4,5,6,7,8}. Тогда подмножество {(a,2),(c,3),(d,5)} в A x B является бинарным отношением между множествами A и B.

3.Перестановки с повторениями и без.

перестановка — это упорядоченный набор чисел 1,2…n  обычно трактуемый как биекция на множестве A, которая числу i ставит в соответствие i-й элемент из набора. Число n при этом называется порядком перестановки.

Число всех перестановок порядка n равно n!.

Рассмотрим n элементов m различных типов, причем в каждом типе все элементы одинаковы. Тогда перестановки из всех этих элементов с точностью до порядка следования однотипных элементов называются перестановками с повторением.

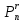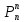1) Число всех упоряд. выборок без повторений объёма r из n-элементного множ. опред:=n((n-1)…(n-r+1), если n=r :=n!

2) Число всех упоряд. выборок c повторениями объёма r из n-элементного множ. опред: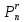=n^r

Пример:A={1,2,3}r=2

1)все упоряд. выборки без повторений от объёма 2: (1,2),(2,1),(1,3),(3,1),(2,3),(3,2);

2)с повторениями (1,1),(2,2),(3,3), (1,2),(2,1),(1,3),(3,1),(2,3),(3,2);

4.Сочетания с повторениями и без.

сочетанием из n по k называется набор k элементов, выбранных из данного множества, содержащего n различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

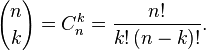
Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.

Число сочетаний с повторениями из n по k равно биномиальному коэффициенту