
- •1.Понятие об управлении процессами. Структура и технология управления надёжностью машин
- •2.Анализ методов обеспечения надёжности при проектировании, производстве и ремонте
- •2.1. Анализ методов обеспечения надёжности элементов
- •2.2. Анализ методов обеспечения надёжности систем при существующей элементной базе
- •3. Методы расчета показателей надежности
- •3.1 Структурные методы расчета н
- •3.1. Б) Расчет показателей безотказности при резервировании замещением
- •3.1. В) Расчет показателей безотказности при постоянном раздельном резервировании с учетом изменения условий работы элементов
- •3.3 Физические (параметрические) методы расчета надежности.
3.1. В) Расчет показателей безотказности при постоянном раздельном резервировании с учетом изменения условий работы элементов
Рассмотрим решение поставленной задачи на примере объекта, ССН которого представлена на рис. 1.5.
Исходные данные:
- известны
интенсивности отказов элементов:
![]() - если оба элемента рбтс; и
- если оба элемента рбтс; и![]() - если один из них отказал.
- если один из них отказал.
- для выполнения объектом заданных функций достаточно одного элемента.
ОпределитьВБР объектаP(t).
Допущение:
режим эксплуатации объекта стационарный,
поэтому![]()
![]()
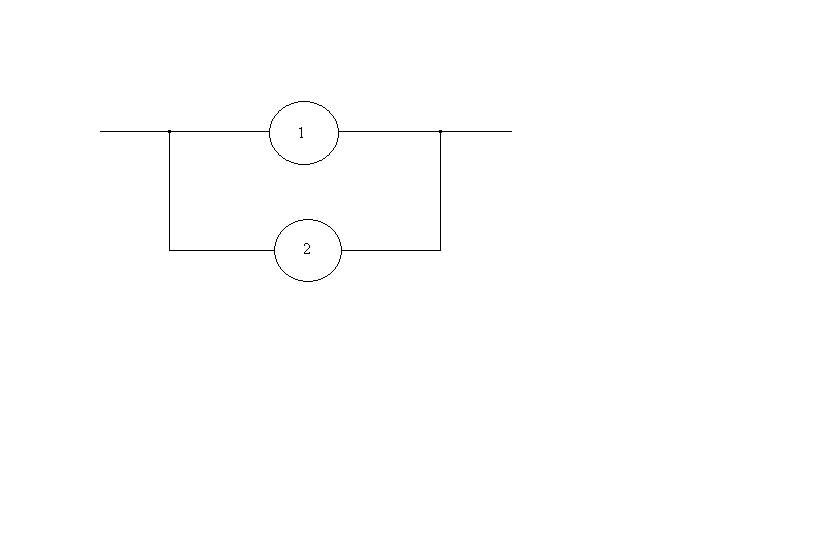



Рис. 1.5. ССН объекта и диаграмма его возможных работоспособных состояний.
Решение– Расчет вероятности безотказной работы.
Пусть событие Н – безотказная работа объекта в течение наработки t. Это событие может свершиться при следующих благоприятных гипотезах (см. рис. 1.5):
![]() - не откажут оба
элемента в течение наработки t.;
- не откажут оба
элемента в течение наработки t.;
![]() - при некоторой
наработке
- при некоторой
наработке
![]() откажет первый элемент, а второй
проработает безотказно в течение
наработкиt;
откажет первый элемент, а второй
проработает безотказно в течение
наработкиt;
![]() - при некоторой
наработке
- при некоторой
наработке
![]() откажет второй элемент, а первый
проработает безотказно в течение
наработкиt.
откажет второй элемент, а первый
проработает безотказно в течение
наработкиt.
Очевидно, событие
Н можно представить как логическую
сумму событий и тогда вероятность
события Н (ВБР) будет
![]()
Определим вероятности этих событий
![]()
![]()
![]()
![]()

С учётом того, что![]() вероятность безотказной работы объекта
будет определена зависимостью:
вероятность безотказной работы объекта
будет определена зависимостью:

Проинтегрировав
![]()
![]() в пределах от нуля до бесконечности,
получим
в пределах от нуля до бесконечности,
получим
 .
.
Принципиально данная задача может быть решена для объекта любой сложности, при этом если и будут трудности, то только математического плана.
3.2. Методы прогнозированияоснованы на использовании данных о значениях ПН объектов-аналогов, находящихся и (или) находившихся в эксплуатации и тенденциях их изменения.
Эти методы используются для обоснования требований к уровню надежности разрабатываемых объектов. При этом значения показателей надежности рассчитываются, как правило, по статистическим моделям полиномиального вида.
![]()
где y– прогнозируемый показатель надежности;
xr–r-й конструктивно-технологический фактор объекта, оказывающий существенное влияние на прогнозируемый показатель надежности;(Т.к. надёжность это свойство объекта, то ПН являются функцией свойств его конструкции и м. б. технологии. Например, Тв при ремонте методом замены определяется: - доступностью – числом предварительно снимаемых элементов; - легкосъёмностью – числом крепежа на заменяемых элементах; -массой заменяемых элементов и т. п.)
lr- показатель степени, учитывающий совместно с коэффициентомarстепень влиянияr-го фактора на значение показателя надежности;
a0, ….ar - коэффициенты модели, значения которых определяются в рамках корреляционно-регрессионного анализа методом наименьших квадратов по значениямyjиxrj объектов-аналогов,j=1,...,m.
Сущность МНК
Рассмотрим на более простом примере, когда y является функцией только одного фактораx.Тогда исходные данные, собранные по объектам-аналогам, будут иметь вид
|
X |
X1 |
X2 |
. . . |
Xj |
. . . |
Xm |
|
Y |
Y1 |
Y2 |
. . . |
Yj |
. . . |
Ym |
Задача же как мы помним заключается в получении модели вида (1), в данном случае в виде двучлена
![]() .
.
Проведём графическую
аппроксимацию данных таблицы. Для этого
нанесём точки XjиYjна плоскость координатXOY.
В данном случае теоретический закон
имеет вид прямой линии, уравнение которой![]() или
или![]() .
.
Следует заметить,
что не все опытные точки совпадают с
графиком, а имеют некоторые отклонения
от него
![]() .
Очевидно, что эта линия должна
располагаться на плоскости координат
так, чтобы отклонения, точнее сумма
отклонений опытных точек
.
Очевидно, что эта линия должна
располагаться на плоскости координат
так, чтобы отклонения, точнее сумма
отклонений опытных точек![]() от
неё были минимальными. Чем определяется
положение этой линии на плоскости?
Значениями коэффициентов и их знаками.
Следовательно, задача состоит в отыскании
именно таких коэффициентов. Как её
решить?
от
неё были минимальными. Чем определяется
положение этой линии на плоскости?
Значениями коэффициентов и их знаками.
Следовательно, задача состоит в отыскании
именно таких коэффициентов. Как её
решить?
x
Выразим сказанное математически и найдём этот минимум.

Как это сделать? Самый простой приём, известный в математике это взятие первой производной от функции, приравнивание её к нулю и нахождение такого значения аргумента X, при котором функция обращается в минимум.
Тогда

После несложных преобразований , получим

Решив эту систему
уравнений, получим значения искомых
коэффициентов
![]() найденных при условии обеспечения
минимума ошибки адекватности принятой
модели. Т. о. задача решена.
найденных при условии обеспечения
минимума ошибки адекватности принятой
модели. Т. о. задача решена.
В общем случае решение задачи приводится ниже:
1). Имеются данные о значениях yj и xrj , j=1,...,m, собранные наблюдением за объектами-аналогами.
2). Эти данные аппроксимируются моделью вида (1) так, чтобы сумма квадратов отклонений опытных точек от поверхности (линии), заданной моделью, была минимальной, то есть:

Отсюда система нормальных уравнений R+1 с R+1 неизвестными a0 ,…aR .
В качестве примера такой моделиможно привести уравнение связи, полученное профессором Есиным для машин гусеничного типа, устанавливающее естественную связь между средним временем их восстановленияТВиКТФ.
X1– масса проектируемого образца, т.
X2 - удельная мощность, кВт/кг.
X3– число выполняемых машиной функций.
![]()
Зная значения X1,X2,X3 (они должны быть известны в техническом задании), подставим их в модель и получаемпрогнозную оценкуТВдля перспективного образца, которая после критического анализа закладывается в техническое задание.
