
- •1.Понятие об управлении процессами. Структура и технология управления надёжностью машин
- •2.Анализ методов обеспечения надёжности при проектировании, производстве и ремонте
- •2.1. Анализ методов обеспечения надёжности элементов
- •2.2. Анализ методов обеспечения надёжности систем при существующей элементной базе
- •3. Методы расчета показателей надежности
- •3.1 Структурные методы расчета н
- •3.1. Б) Расчет показателей безотказности при резервировании замещением
- •3.1. В) Расчет показателей безотказности при постоянном раздельном резервировании с учетом изменения условий работы элементов
- •3.3 Физические (параметрические) методы расчета надежности.
3.1. Б) Расчет показателей безотказности при резервировании замещением
Резервирование замещением – это резервирование, при котором функции основного элемента передаются резервному только после отказа основного элемента. при этом резервные элементы до включения, как правило, могут находиться в облегченном или ненарушенном режиме (например, запасные части).
Расчет показателей безотказности при резервировании замещением рассмотрим на следующем примере.
Дано: -объект, состоящий из одного основного и «m» резервных элементов, рис.1,3
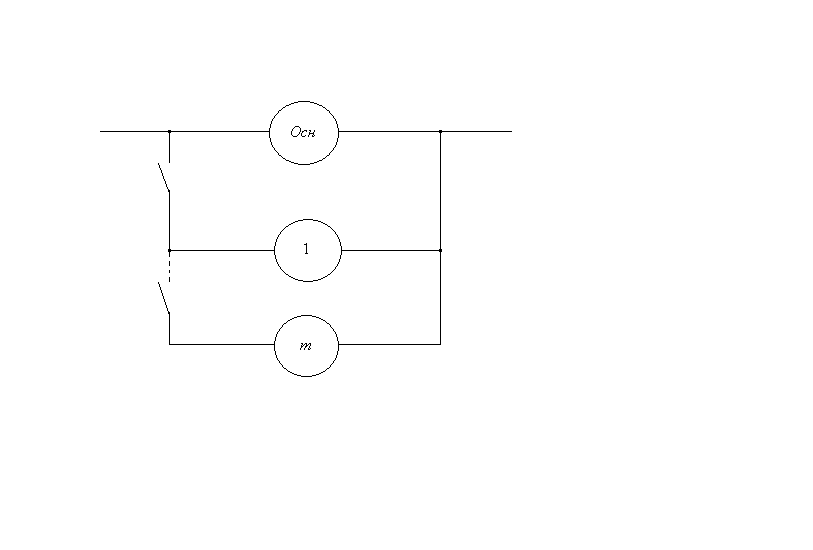
Рис.1.3.
-интенсивность
отказов элементов
![]() ;
;
-так как
![]() то модель функционирования такого
объекта можно представить в виде: при
отказе основного элемента включается
первый резервный, после отказа первого
– второй резервный и т.д.
то модель функционирования такого
объекта можно представить в виде: при
отказе основного элемента включается
первый резервный, после отказа первого
– второй резервный и т.д.
Определить показатели БО :
![]() ;
;![]() ;
;
Допущения:
1. Поток отказов элементов простейший.
2. Переключатели абсолютно надежны.
Вопрос: Когда объект будет работоспособным?
Условием нормального функционирования объекта является работоспособность хотя бы одного элемента. Реализация этого условия возможна при разных состояниях объекта.
Проведем рассуждения о возможных ситуациях РБТС объекта.
Пусть Н – событие, заключающееся в безотказной работе объекта. Оно будет иметь место при следующих событиях:
- при
![]() - событие, заключающееся в безотказной
работе основного элемента;
- событие, заключающееся в безотказной
работе основного элемента;
- или при
![]() - событии, заключающемся в отказе одного
(основного) элемента;
- событии, заключающемся в отказе одного
(основного) элемента;
- или при
![]() - событии, заключающемся в отказе двух
элементов (основного и первого резервного
элемента);
- событии, заключающемся в отказе двух
элементов (основного и первого резервного
элемента);
- или при ………………………
- или при
![]() - событии, заключающемся в отказеmэлементов (основного и первого,
второго,…,(m-1) резервных
элементов).
- событии, заключающемся в отказеmэлементов (основного и первого,
второго,…,(m-1) резервных
элементов).
Тогда событие Н
будет иметь место при возникновении
хотя бы одного события
![]() ,
что по определению соответствует суммеmсобытий, т.е.
,
что по определению соответствует суммеmсобытий, т.е.![]() ,
т.к. по определению «Суммой нескольких
событий называется событие, состоящее
в появлении хотя бы одного из этих
событий».
,
т.к. по определению «Суммой нескольких
событий называется событие, состоящее
в появлении хотя бы одного из этих
событий».
Так как рассматриваемые события случайны, определим их вероятности
![]()
События
![]() являются несовместными. В соответствии
с теоремой сложения вероятностей –
вероятность суммы несовместных событий
равна сумме вероятностей этих событий.
являются несовместными. В соответствии
с теоремой сложения вероятностей –
вероятность суммы несовместных событий
равна сумме вероятностей этих событий.
![]() ,
,
где:
![]() - вероятность того, что откажут ровноiэлементов.
- вероятность того, что откажут ровноiэлементов.
Известно, что в условиях простейшего потока отказов случайное число отказов для резервирования замещением подчиняется распределению Пуассона, в соответствии с которым вероятность появления ровно iсобытий (в данном случае отказов) равна:
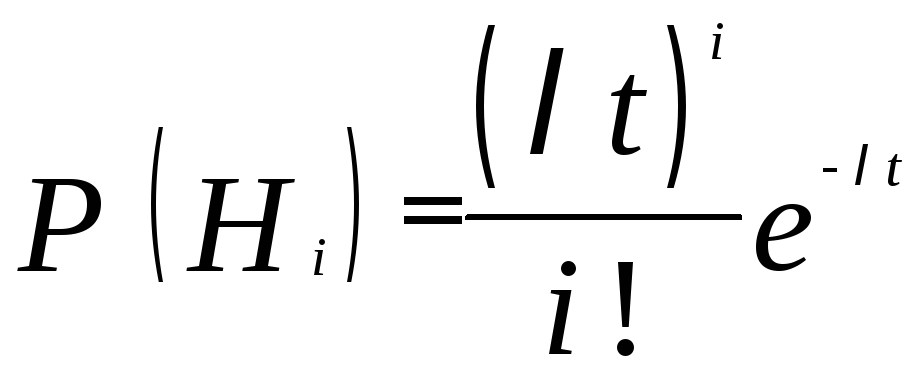 ,
тогда
,
тогда 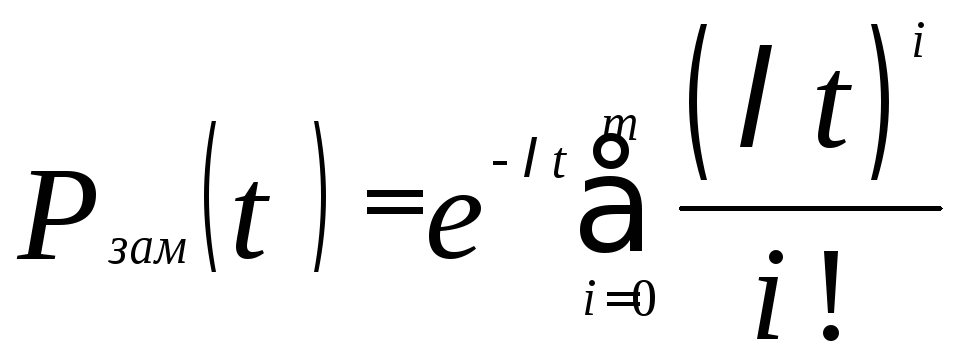
К данной схеме
может быть приведен любой объект,
состоящий из nпоследовательно
(в смысле надежности) соединённых
элементов и имеющийmтаких же резервных цепей (рис. 1.4 ). В
самом деле,nпоследовательных
элементов можно заменить одним с
интенсивностью отказов![]()

Рис. 1.4.
Тогда ВБР этого
объекта вычисляется по зависимости 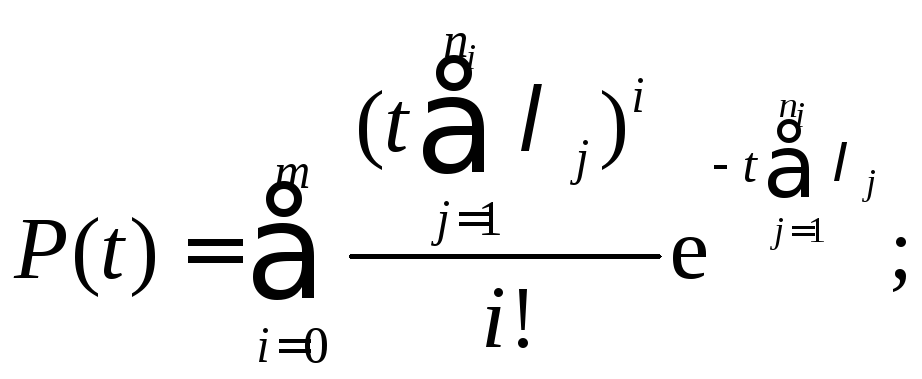
Если все элементы в каждой цепи будут равнонадёжны, то его ВБР можно вычислить по зависимости
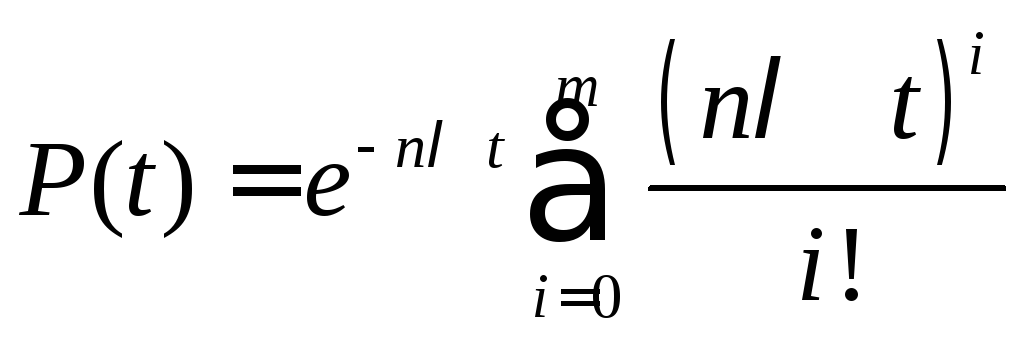
Средняя наработка до отказа определяется по зависимости:
![]()
Подставив сюда
выражение
![]() и
проинтегрировав, получим:
и
проинтегрировав, получим:
![]()
или ![]()
Этот же результат
можно получить из простых рассуждений,
представив себе функционирование
объекта. Основной элемент будет иметь
среднюю наработку равную
![]() ,
первый резервный -
,
первый резервный -![]() и т.д. Поскольку число элементов (m+1),
то средняя наработка объекта равна
сумме средних наработок (m+1)
элементов, что и выражают последние две
формулы.
и т.д. Поскольку число элементов (m+1),
то средняя наработка объекта равна
сумме средних наработок (m+1)
элементов, что и выражают последние две
формулы.
