3.1 Структурные методы расчета н

– это методы прямого вычисления Н, объектов по известной Н, их элементов.

Необходимое условие их применения – независимость отказов элементов. Они являются основными методами расчета показателей БО, РП и КПН объектов, поддающихся разукрупнению на элементы, Н которых на момент расчета уже известна.

Их применяют также для расчета показателей Д и объектов, критериикоторых выражаются через Д иих элементов.

Таким образом, структурные методы дают приемлемые результаты при расчете Н. электрических, электронных, р/эл-х объектов, а также ряда механических систем, разукрупненных до уровня конструктивно-функциональных единиц (узлы гидросистем, коробка передач, бортовой редуктор, двигатель и т.п.), отказы которых являются независимыми.

Расчет Нструктурными методамивключает:

- представление О в виде структурной схемы, т.е. в виде совокупности определенным образом соединенных в смысле Н элементов (составление ССН);

- описание ССН адекватной математической моделью, позволяющей в рамках принятых допущений вычислить ПН О по данным о Н его элементов.

3.1.а) Расчет показателей безотказности при постоянном резервировании

При постоянном резервировании все элементы находятся под нагрузкой и поэтому нельзя выделить в объекте основные и резервные элементы. Все они «равноправны».

Методику расчета ПБ при постоянном резервировании будем рассматривать на примере восстанавливаемых объектов.

Известны:

-конструкция объекта (его элементный состав и структура);

-интенсивность отказов элементов – ,i=1,…,n.

Определить:

-ВБР объекта в течение заданной наработки t–P(t);

-среднюю наработку до 1-го отказа – Т₁;

-параметр потока отказов объекта – Ω(t).

Допущение:

-поток отказов элементов – простейший.

Уяснение задачи:

1.Вид объекта – восстанавливаемый

2.Так как ПБО рассчитываются до 1-го отказа(например с целью установления гарантийной наработки), то очевидно, что

Т₁=Тс для НВО

3.Так как поток отказов элементов простейший, то:

- отказы элементов – события независимые;

4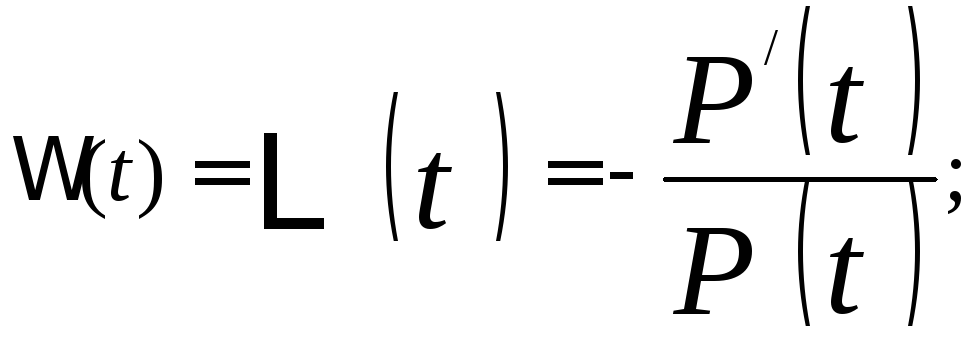.В данной задаче достаточно определить Р(t) в виде функции, т.к. остальные показатели можно вычислить черезP(t) по следующим зависимостям:

.

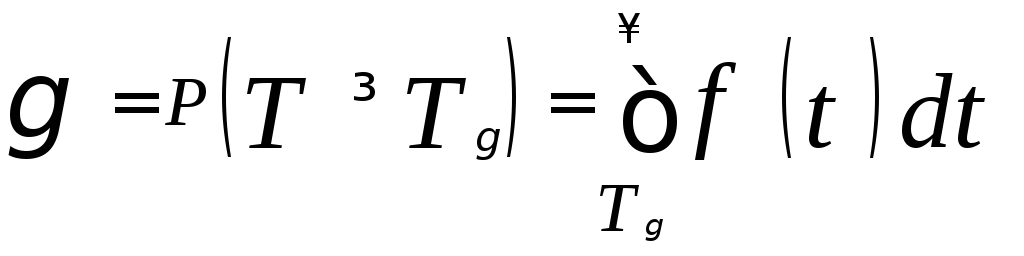В дальнейшем покажем только методику определения вероятности безотказной работы.

Задача I. Рассмотрим объект, состоящий из «n» последовательно соединенных (в смысле надежности) элементов, вероятность безотказной работы которых равна.

В каком случае эта «цепочка» будет работать?

В том случае, если все элементы работоспособны. Формализуем этот ответ. С этой целью введём: событие А – заключающееся в безотказной работе объекта;

событие А_i– заключающееся в безотказной работеi– го элемента.

Тогда А будет иметь место при совместном выполнении всех событий А_i, что соответствует их произведению, то есть

Так как события А и А_iслучайны, определим их вероятности

,

что в терминах решаемой задачи равносильно

- математическая модель ССН объекта.

Правило 1.При расчете ВБР, цепь последовательно соединенных (в смысле надежности) элементов можно заменить одним элементом с вероятностью безотказной работы равной произведению вероятностей безотказной работы всех элементов этой цепи.

Задача II. Рассмотрим объект, состоящий из «m» параллельно соединенных (в смысле надежности) элементов, вероятность безотказной работы которых равна,j=1,…,m.

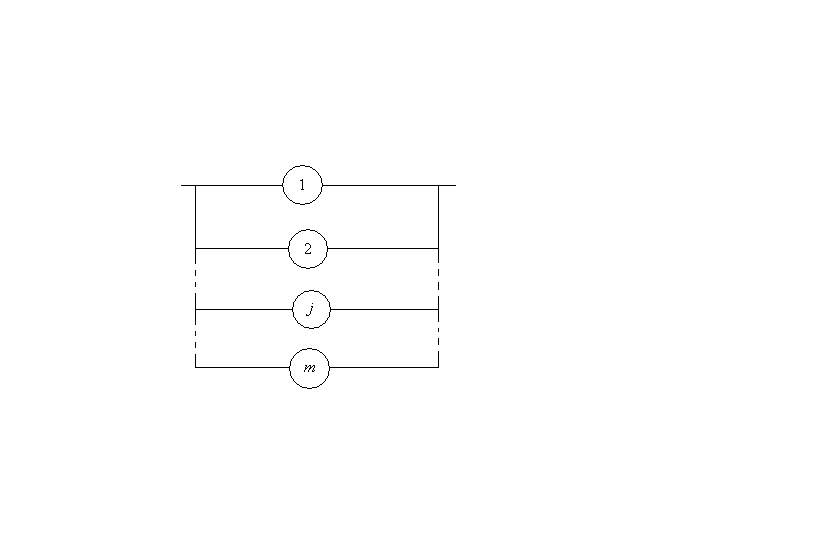
Вопрос: В каком случае откажет эта подсистема?

В том случае, если откажут все элементы. Формализуем этот ответ. С этой целью введём: событие B– заключающееся в отказе подсистемы;

событие Bj– заключающееся в отказеj– го элемента.

Тогда Bбудет иметь место при совместном выполнении всех событийBj, что соответствует их произведению, то есть

Так как события BиBjслучайны, определим их вероятности

,

что в терминах решаемой задачи равносильно

Правило 2.При расчете ВО подсистемы, состоящей из параллельно соединенных (в смысле надежности) элементов, их можно заменить одним, с вероятностью отказа равной произведению вероятностей отказа всех элементов этой подсистемы.

Это выражение легко преобразовать, если учесть, что

Окончательно получим:

- математическая модель ССН подсистемы.

Если все элементы звена равнонадёжны, то последняя зависимость при ЭЗР примет вид

Вычислим среднюю наработку до отказа подсистемы.

Известно, что ОпределимP(t).

Используя правило (П 2), получим:

При ЭЗР имеем: Тогда

Введем переменную

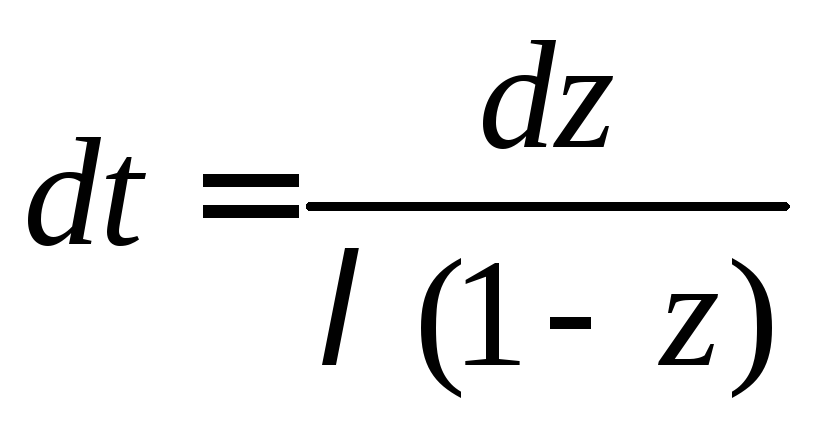
Отсюда

Определим пределы z. Приt=0→z=0;t= ∞ →z=1.

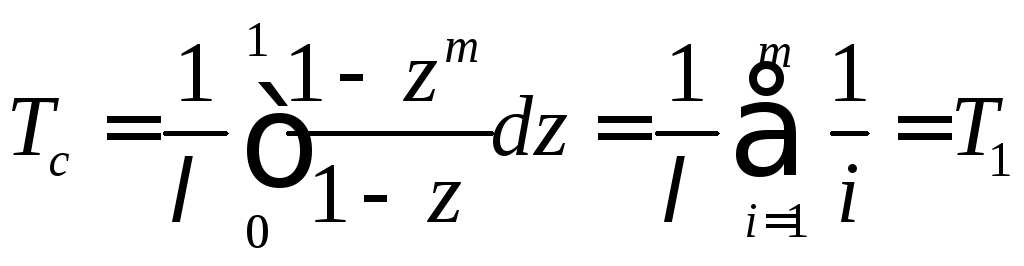
Поэтому

Пользуясь этими правилами, легко рассчитать ВБР любого объекта при постоянном смешанном резервировании.

Рассчитаем ВБР системы, ССН которой приведена на рисунке при известной ВБР её элементов

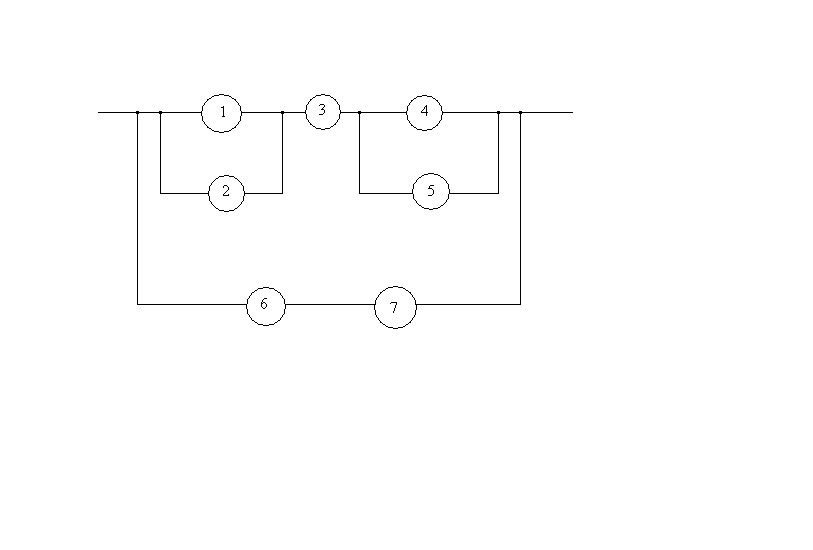
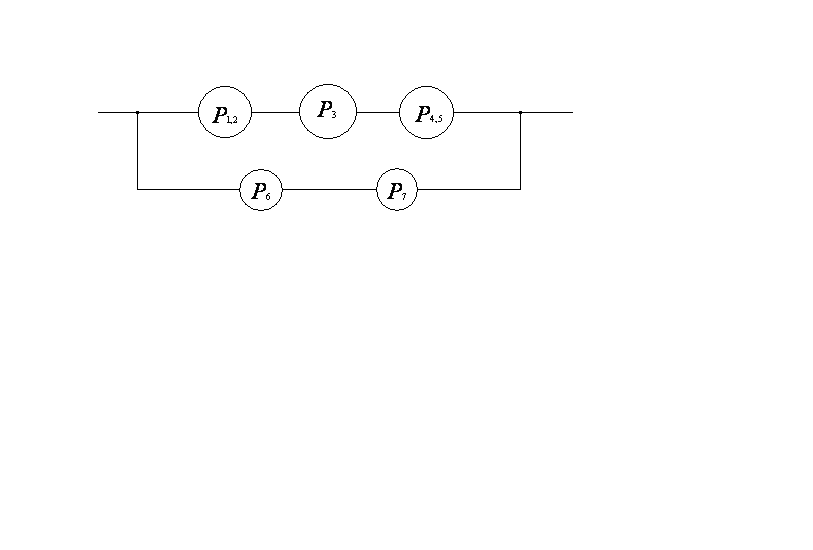
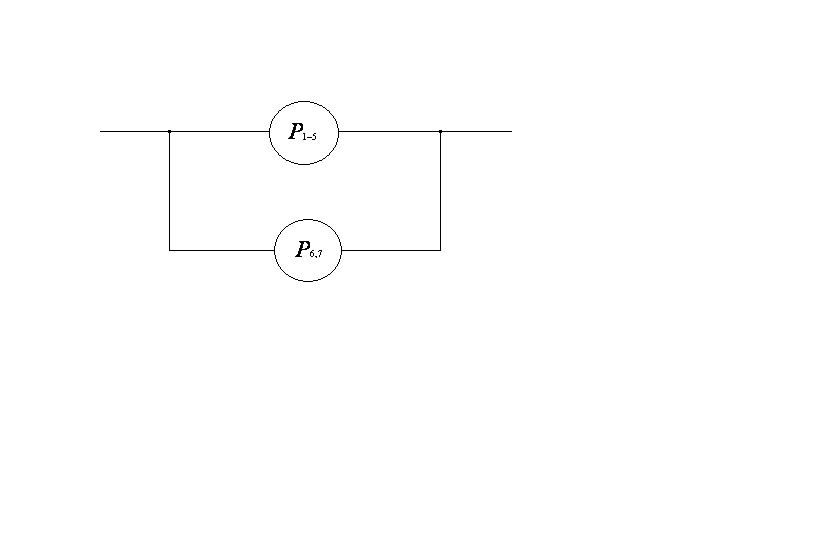
I)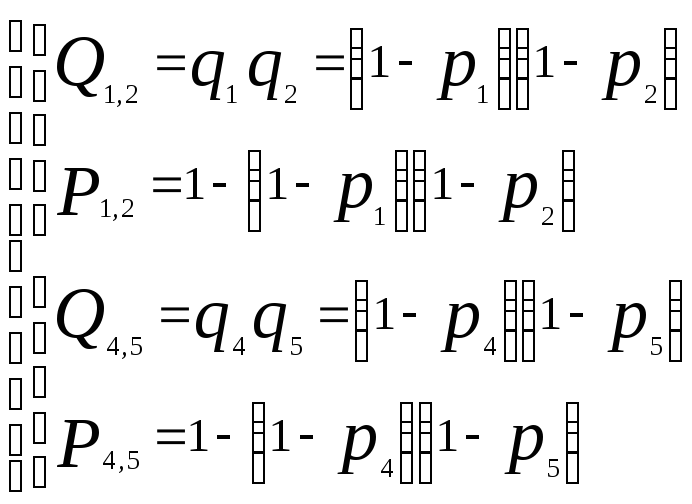

II)

III);

Рассмотренная методика определения ПБО при постоянном резервировании справедлива в том случае, если при отказе какого-либо элемента условия работы других не изменяется.