Теплопроводность через плоские однослойные стенки

Любая практическая задача теплообмена в итоге сводится к вычислению теплового потока или определения температурного поля.

Температурное поле – совокупность значений температур во всех точках тела на выбранный момент времени:

t = t(x, y, z, ), (4)

где x, y, z – координаты.

Стационарное температурное поле характеризуется постоянством температуры в каждой точке тела. Если температура изменяется только по одной координате (х) и не зависит от времени, тогда стационарное температурное поле для однослойной стенки запишется в виде:

t = t(x). (5)

Для определения температурного поля в плоской однослойной стенке используется дифференциальное уравнение теплопроводности без внутренних источников теплоты:

, (6)

где а = – коэффициент температуропроводности, м²/с;с_р– удельная массовая изобарная теплоемкость, Дж/(кг.К);– плотность, кг/м³;= =– оператор Лапласа.

Согласно формулам (5) и (6) дифференциальное уравнение стационарной теплопроводности через плоскую однослойную стенку имеет вид:

. (7)

При последовательном интегрировании уравнения (7) получается:

, t = C₁x + C₂ , (8)

где C₁ и C₂ – константы интегрирования, которые определяются с учетом граничных условийIII- его рода (постоянство температуры на внешних границах тела).

В результате получается уравнение стационарного одномерного температурного поля (рис. 1):

t = t_c1 - (t_c1 - t_c2), (9)

г

Рис. 1. Температурное поле в плоской одно-

слойной стенке

деt_c1, t_c2– температуры на внешних поверхностях плоской стенки;– толщина стенки;х– текущая координата (0  x ).

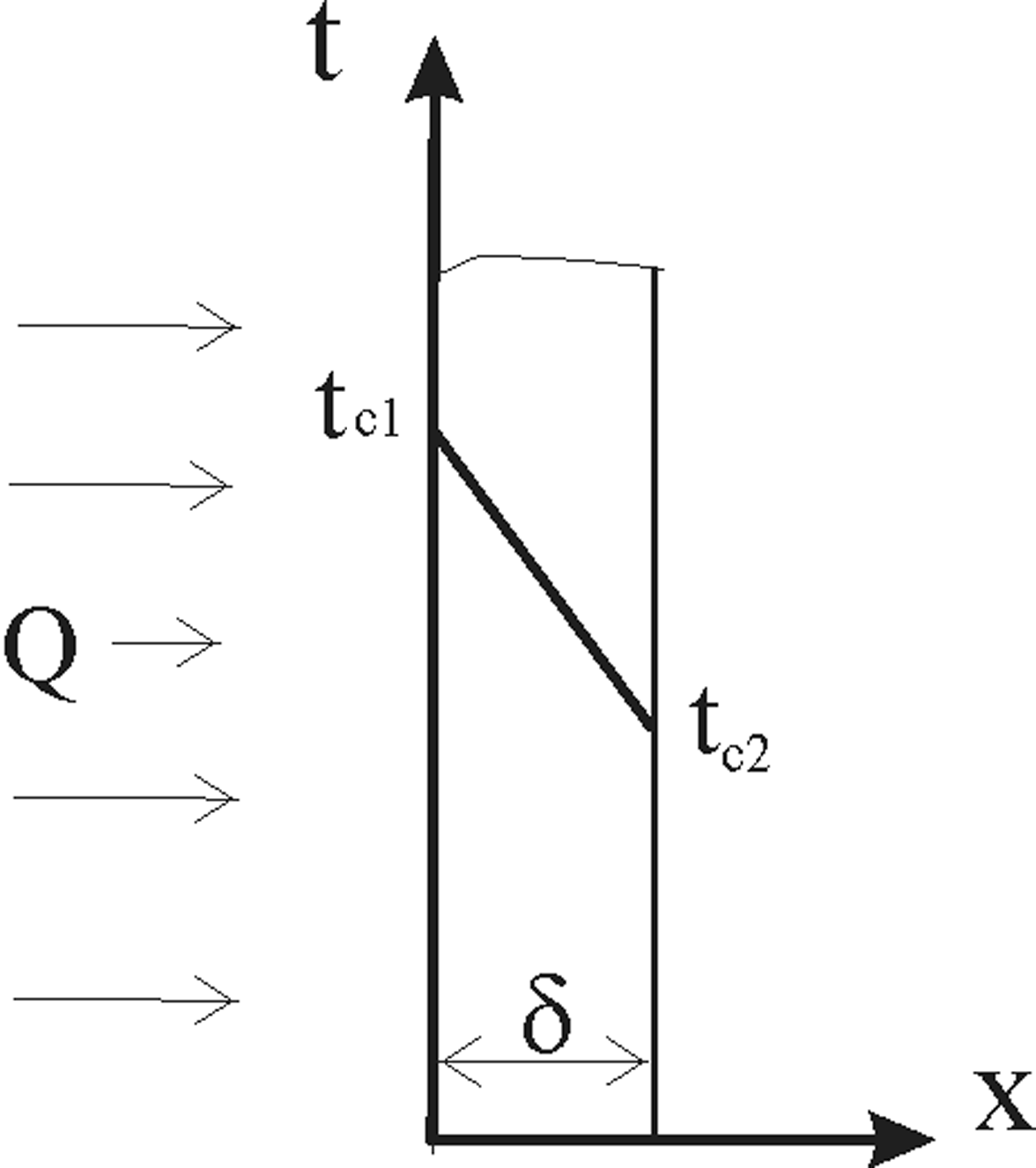
Согласно формуле (9) температурное поле в плоской однослойной стенке представляет собой уравнение прямой линии.

Тепловой поток, передаваемый теплопроводностью через плоскую однослойную стенку, определяется по закону Фурье (1) с учетом выражений температурного поля (8) и (9):

Q = (t_c1 - t_c2)F. (10)

Плотность теплового потока через стенку:

q = (t_c1 - t_c2). (11)

Так как температуры поверхностей плоской стенки постоянны во времени, площадь поверхности плоской стенки одинакова с обеих сторон, то значения теплового потокаQи плотности теплового потокаqне меняются во времени и по толщине стенки.

Формулы для определения теплового потока (10) и плотности теплового потока (11) можно привести к виду:

Q = ,q = , (12)

где ,– полное и удельное термическое сопротивление передачи теплоты теплопроводностью.

Из соотношения (12) видно, что при стационарной теплопроводности перепад температур на плоской стенке прямо пропорционален термическому сопротивлению и обратно пропорционален величине коэффициента теплопроводности.