
- •Содержание
- •ВВЕДЕНИЕ
- •2. РИСКИ СТРАХОВОЙ ОРГАНИЗАЦИИ И ФИНАНСОВЫЕ ИСТОЧНИКИ ИХ ПОКРЫТИЯ
- •3. СТРАТЕГИЧЕСКОЕ УПРАВЛЕНИЕ ФИНАНСОВЫМИ РИСКАМИ СТРАХОВОЙ ОРГАНИЗАЦИИ
- •3.1. ОСНОВЫ СТРАТЕГИЧЕСКОГО УПРАВЛЕНИЯ ФИНАНСОВЫМИ РИСКАМИ
- •3.2. ФУНКЦИИ И МЕХАНИЗМ УПРАВЛЕНИЯ ФИНАНСОВЫМИ РИСКАМИ СТРАХОВЩИКА
- •3.3. СОДЕРЖАНИЕ ПРОЦЕССА СТРАТЕГИЧЕСКОГО УПРАВЛЕНИЯ ФИНАНСОВЫМИ РИСКАМИ
- •4. МЕХАНИЗМЫ УПРАВЛЕНИЯ РИСКАМИ СТРАХОВОЙ ОРГАНИЗАЦИИ
- •4.1. СТРАХОВОЙ АНДЕРРАЙТИНГ
- •4.2. ПЕРЕРАСПРЕДЕЛЕНИЕ РИСКОВ
- •4.3. РЕЗЕРВИРОВАНИЕ
- •4.4. ДИВЕРСИФИКАЦИЯ
- •4.5. ЛИМИТИРОВАНИЕ
- •4.6. ХЕДЖИРОВАНИЕ
- •5. УПРАВЛЕНИЕ РИСКОМ СНИЖЕНИЯ ФИНАНСОВОЙ УСТОЙЧИВОСТИ И ПЛАТЕЖЕСПОСОБНОСТИ СТРАХОВОЙ ОРГАНИЗАЦИИ
- •5.1. ОБЩАЯ ХАРАКТЕРИСТИКА ФИНАНСОВОЙ УСТОЙЧИВОСТИ И ПЛАТЕЖЕСПОСОБНОСТИ СТРАХОВОЙ ОРГАНИЗАЦИИ
- •5.2. ОБЕСПЕЧЕНИЕ ФИНАНСОВОЙ УСТОЙЧИВОСТИ СТРАХОВЫХ ОПЕРАЦИЙ
- •5.3. ПОКАЗАТЕЛИ И МЕТОДИКА ОЦЕНКИ ПЛАТЕЖЕСПОСОБНОСТИ СТРАХОВОЙ ОРГАНИЗАЦИИ
- •6. УПРАВЛЕНИЕ РИСКАМИ ЛИКВИДНОСТИ
- •6.2. РИСК ЛИКВИДНОСТИ
- •7. УПРАВЛЕНИЕ КРЕДИТНЫМ РИСКОМ СТРАХОВОЙ ОРГАНИЗАЦИИ
- •7.1. ПОНЯТИЕ КРЕДИТНОГО РИСКА
- •7.2. ДЕФОЛТ И КРЕДИТНОЕ СОБЫТИЕ
- •7.3. МОДЕЛИ ОЦЕНКИ КРЕДИТНОГО РИСКА
- •7.4. ОСНОВНЫЕ СОСТАВЛЯЮЩИЕ КРЕДИТНОГО РИСКА
- •7.5. МЕТОДЫ ОЦЕНКИ ВЕРОЯТНОСТИ ДЕФОЛТА
- •7.6. ПОДВЕРЖЕННОСТЬ КРЕДИТНОМУ РИСКУ
- •7.7. ОЦЕНКА РИСКА ДЕФОЛТА ДЛЯ ПОРТФЕЛЯ АКТИВОВ
- •7.8. УПРАВЛЕНИЕ КРЕДИТНЫМИ РИСКАМИ
- •7.9. КРЕДИТНЫЕ ПРОИЗВОДНЫЕ ИНСТРУМЕНТЫ
- •8. УПРАВЛЕНИЕ ИНВЕСТИЦИОННЫМ РИСКОМ
- •8.1. ПРИНЦИПЫ ИНВЕСТИЦИОННОЙ ДЕЯТЕЛЬНОСТИ СТРАХОВОЙ ОРГАНИЗАЦИИ
- •8.2. ФОРМУЛИРОВКА ИНВЕСТИЦИОННЫХ ЦЕЛЕЙ
- •8.3. ФОРМИРОВАНИЕ ИНВЕСТИЦИОННОЙ ПОЛИТИКИ И ИНВЕСТИЦИОННОЙ СТРАТЕГИИ СТРАХОВОЙ ОРГАНИЗАЦИИ
- •8.4. АНАЛИЗ АКТИВОВ И ПЕРИОДА ИНВЕСТИРОВАНИЯ
- •8.5. ПОДХОДЫ К ОПТИМИЗАЦИИ ИНВЕСТИЦИОННОЙ ПОЛИТИКИ СТРАХОВЩИКА
- •8.6. ФОРМИРОВАНИЕ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ И ЕГО ПЕРЕСМОТР
- •8.7. ОЦЕНКА ЭФФЕКТИВНОСТИ ИНВЕСТИЦИОННОЙ ДЕЯТЕЛЬНОСТИ
- •II. ИНВЕСТИЦИОННЫЕ КАЧЕСТВА ФИНАНСОВЫХ ИНСТРУМЕНТОВ В СВЕТЕ УПРАВЛЕНИЯ РИСКОМ
- •9. ОБЛИГАЦИИ
- •9.1. ОПРЕДЕЛЕНИЕ КУРСОВОЙ СТОИМОСТИ ОБЛИГАЦИИ
- •9.2. ОПРЕДЕЛЕНИЕ СУММАРНЫХ ДОХОДОВ ПО ОБЛИГАЦИИ
- •9.3. ДЮРАЦИЯ КАК ПОКАЗАТЕЛЬ РИСКА ОБЛИГАЦИИ
- •9.4. КРИВИЗНА ОБЛИГАЦИИ
- •10. АКЦИИ
- •10.1. ОПРЕДЕЛЕНИЕ КУРСОВОЙ СТОИМОСТИ АКЦИИ
- •10.2. ОПРЕДЕЛЕНИЕ ДОХОДНОСТИ АКЦИИ
- •10.3. РИСК АКЦИИ
- •10.5. МОДЕЛЬ ДОХОДНОСТИ АКЦИИ
- •11. УПРАВЛЕНИЕ РИСКОМ ПОРТФЕЛЯ ФИНАНСОВЫХ ИНСТРУМЕНТОВ ИНВЕСТИРОВАНИЯ
- •11.1. ИММУНИЗАЦИЯ ПОРТФЕЛЯ ОБЛИГАЦИЙ
- •11.2. ИСПОЛЬЗОВАНИЕ ИНСТРУМЕНТОВ СРОЧНОГО РЫНКА ДЛЯ ХЕДЖИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ
- •11.3. ХЕДЖИРОВАНИЕ САМОЙ ДЕШЕВОЙ ОБЛИГАЦИИ
- •11.5. ХЕДЖИРОВАНИЕ ПОРТФЕЛЯ ОБЛИГАЦИЙ С ПОМОЩЬЮ ПОКАЗАТЕЛЯ ДЮРАЦИИ
- •11.6. ХЕДЖИРОВАНИЕ ПОРТФЕЛЯ ОБЛИГАЦИЙ С ПОМОЩЬЮ ПОКАЗАТЕЛЕЙ ДЮРАЦИИ И КРИВИЗНЫ
- •III. СТОИМОСТЬ ПОД РИСКОМ
- •12. КОНЦЕПЦИЯ VAR
- •12.1. ИЗМЕРЕНИЕ РЫНОЧНЫХ РИСКОВ
- •12.2. ОПРЕДЕЛЕНИЕ VAR
- •12.3. ВЕРИФИКАЦИЯ МОДЕЛЕЙ РАСЧЕТА VAR ПО ИСТОРИЧЕСКИМ ДАННЫМ
- •12.4. АНАЛИТИЧЕСКИЙ (ИЛИ ПАРАМЕТРИЧЕСКИЙ) МЕТОД
- •12.5. МЕТОД ИСТОРИЧЕСКОГО МОДЕЛИРОВАНИЯ (ИЛИ МОДЕЛИРОВАНИЯ ПО ИСТОРИЧЕСКИМ ДАННЫМ)
- •12.6. МЕТОД ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ (МЕТОД МОНТЕ-КАРЛО)
- •12.8. ПРОВЕРКА НА УСТОЙЧИВОСТЬ (СТРЕСС-ТЕСТИРОВАНИЕ)
- •ЗАКЛЮЧЕНИЕ
- •СПИСОК ОСНОВНОЙ ЛИТЕРАТУРЫ
- •СПИСОК ДОПОЛНИТЕЛЬНОЙ ЛИТЕРАТУРЫ
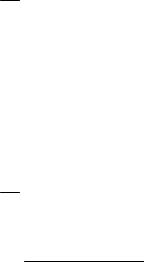
10.2. ОПРЕДЕЛЕНИЕ ДОХОДНОСТИ АКЦИИ
Принимая решение купить акцию на определенный период, инвестору необходимо оценить возможную доходность его операции. После завершения операции следует определить ее фактическую доходность. До- ходность операции с акцией, которая занимает не- сколько лет, можно ориентировочно определить по формуле:
|
Ps Pb / n |
|
|
|
r |
div |
, |
||
Ps Pb / 2 |
||||
|
|
|||
где: r – доходность от операции с акцией; Ps – цена продажи акции;
Pb – цена покупки акции;
div – средний дивиденд за n лет (он определяется как среднее арифметическое);
n – число лет от покупки до продажи акции.
Пример
Инвестор купил акцию за 200 руб. и продал через три года за 300 руб.; за первый год ему выплатили дивиденд в размере 10 руб., за второй – 15 руб., за третий – 20 руб. Определить до- ходность операции вкладчика.
Решение Средний дивиденд за три года равен:
div 10 15 20 15 руб. 3
Доходность операции составила:
r 300 200 / 3 15 0,1933 или 19,33% 300 200 / 2
Если покупка и продажа акции происходят в рамках года, то доходность операции можно определить по формуле:
344

r Ps Pb div 365 , Pb t
где t – число дней с момента покупки до продажи ак- ции.
Если за прошедший период дивиденд на акцию не выплачивался, он исключается из формулы.
Вопросы для самоконтроля
1.Номинал облигации, до погашения которой ос- тается 5 лет, равен 1000 руб., купон 20%, выплачивается один раз в год. Определите цену облигации, чтобы она обеспечила покупателю доходность до погашения в размере 30% годовых. (Ответ: 512,89 руб.)
2.Номинал бескупонной облигации, до погашения которой остается 6 лет, равен 1000 руб. Определите цену облигации, чтобы она обеспечила покупателю доходность до погашения в размере 30% годовых. (От-
вет: 207,18 руб.)
3.Определите цену ГКО, чтобы она обеспечила покупателю доходность до погашения в размере 30% годовых. До погашения ГКО остается 60 дней.
(Ответ: 95, 30%)
4.Определите доходность ГКО, если ее цена равна 90% и до погашения остается 120 дней. (Ответ: 30,75%)
5.Определите текущую доходность купонной об- лигации, если купон равен 100 руб., цена – 950 руб. (Ответ: 10,53%)
6.Номинал бескупонной облигации равен 1000 руб., цена – 800 руб., до погашения остается три года. Определите доходность до погашения облигации. (От-
вет: 7,72%)
7.До погашения бескупонной облигации 6 лет, до- ходность до погашения составляет 20%. Определите модифицированную дюрацию облигации.
(Ответ: 5 лет)
345
8.Номинал купонной облигации 1000 руб., купон- ная ставка – 10% и выплачивается один раз в год. До погашения облигации три года. На рынке ее цена равна номиналу. Определите: а) дюрацию Макоэля; в) моди- фицированную дюрацию; с) на какую сумму упадет цена облигации при росте ее доходности до погашения на 0,02%.
(Ответ: а) 2,74 года; в) 2,49 года; с) 0,5 руб.)
9.Инвестор покупает облигацию за 950 руб., ее но- минал равен 1000 руб., купон – 10%, до погашения ос- тается четыре года. Он полагает, что за этот период сможет инвестировать купоны под 12%. Определите: а) общую сумму средств, которые вкладчик получит по облигации, если продержит ее до момента погашения; б) реализованный процент за указанный период. (От-
вет: а) 1477,93 руб.; б) 11,68%)
10.На акцию выплачен дивиденд в размере 100 руб. Среднегодовой темп прироста дивиденда равен 3%. Определите размер дивиденда, который можно ожи- дать через три года. (Ответ: 112,55 руб.)
11.На акцию был выплачен дивиденд в размере 100 руб. Темп прироста дивиденд равен 5%. Доходность, соответствующая риску инвестирования финансовых ресурсов в данную акцию, равна 35%. Определить цену акции.
(Ответ: 350 руб.)
12.Инвестор планирует купить акции роста. Он полагает, что первый дивиденд будет выплачен через пять лет и составит 100 руб. Темп прироста прибыли компании 5%. Доходность, соответствующая риску ин- вестирования финансовых ресурсов в данную компа- нию, равна 30%. Определите стоимость акции. (Ответ: 140,05 руб.)
13.Инвестор купил акцию за 500 руб. и через 100 дней продал за 600 руб. За этот период на акцию был
346

выплачен дивиденд в размере 50 руб. Определите до- ходность операции инвестора? (Ответ: 109,5%)
10.3. РИСК АКЦИИ
В финансовой теории и практике в качестве меры риска финансового актива принимаются такие показа- тели, как стандартное отклонение и дисперсия его до- ходности. В качестве синонима понятия «стандартное отклонение» используют также термин «волатиль-
ность». Стандартное отклонение и дисперсия доходности ак- ции говорят о степени возможного разброса фактической доход- ности акции вокруг ее средней доходности.
Пусть имеются значения доходности акции за n лет. За первый год она составила величину r1 , за вто-
рой − r2 и т. д., за n-ый год – rn. Проведем расчеты в
несколько шагов.
ШАГ 1. Определяем среднее значение доходности акции за n лет. Это просто средняя арифметическая значений ее доходности за этот период:
r r1 r2 r3 ... rn n
Если использовать знак для компактной фор- мы записи суммирования, формула примет вид:
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
ri |
|
|
r |
|
i 1 |
, |
|||
|
n |
||||||
|
|
|
|
|
|
|
|
где: |
|
|
– средняя доходность акции; |
||||
r |
|||||||
n – |
количество лет, за которые наблюдались зна- |
||||||
|
|
|
|
|
|
|
n |
чения |
|
доходности; знак суммы ri показывает, что |
|||||
i 1
осуществляется суммирование всех значений показате- ля r с коэффициентами от величины i до n .
347

ШАГ 2. Определяем для каждого года отклонение фактического значения доходности от ее средней ве-
личины и возводим полученные данные в квадрат. Для |
|||||||
первого |
года получаем: r1 |
|
2 , для второго года – |
||||
r |
|||||||
r2 |
|
2 |
и т. д., для n гогода rn |
|
2 . |
||
r |
r |
||||||
ШАГ 3. Суммируем квадраты отклонений:
r1 r 2 r2 r 2 ... rn r 2 n ri r 2
i 1
ШАГ 4. Делим полученную сумму на количество лет:
n ri r 2
2 i 1
n
Величина 2 является дисперсией доходности ак- ции в расчете на год. Как уже отмечалось, дисперсия является показателем рассеяния фактических значений доходности акции вокруг ее средней величины. Раз- мерность дисперсии представляет собой квадрат до- ходности акции. Если в формуле мы учитываем доход- ность в процентах, то размерность дисперсии – это процент в квадрате. Показателем такой размерности не всегда удобно пользоваться, поскольку сама доходность акции измеряется в процентах. Поэтому из дисперсии извлекают квадратный корень и получают стандартное отклонение доходности:
 2 ,
2 ,
где – стандартное отклонение доходности акции. Стандартное отклонение измеряется уже в процентах, то есть в тех же единицах, что и доходность.
Если предположить, что при расчете дисперсии и стандартного отклонения мы учли все существующие значения доходности, то есть всю генеральную сово-
348

купность случайной переменной, то полученная по
|
|
n |
|
|||
|
|
ri |
|
2 |
|
|
|
|
r |
|
|||
формуле 2 |
|
i 1 |
дисперсия называется гене- |
|||
n |
||||||
|
|
|
||||
ральной дисперсией, а стандартное отклонение – соответ-
ственно генеральным стандартным отклонением. Однако на практике невозможно учесть все фактические зна- чения доходности акции. Поэтому оценку данных по- казателей проводят на основе только части этих значе- ний, то есть на основе некоторой выборки данных. Тогда в результате расчета получают так называемую вы-
борочную дисперсию.
Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то она будет приво- дить к систематическим ошибкам, занижая значение генеральной дисперсии. Это происходит потому, что при расчете отклонения его считают не от истинного среднего значения переменной, а от выборочного. Вы- борочное же среднее непосредственно находится в центре выборки и поэтому отклонения от него выбо- рочных данных в среднем меньше, чем от действитель- ного среднего значения переменной в генеральной со- вокупности. Чтобы скорректировать данную погрешность, переходят к так называемой исправленной дисперсии. Она определяется по следующей формуле:
n ri r 2
2 i 1
n 1
Формулы определения дисперсий отличаются толь- ко знаменателем. Данная корректировка осуществляет- ся для того, чтобы получить несмещенную оценку
349
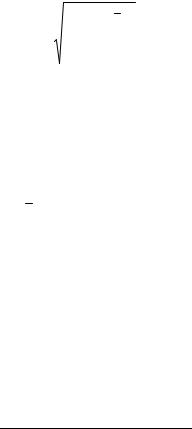
генеральной дисперсии3. Корректировка является су- щественной, если оценку дисперсии проводят на осно- ве небольшого количества данных. При большом объ- еме выборки различие в расчетах бывает незначительным. На практике пользуются исправлен- ной дисперсией, если количество наблюдений меньше 30. Соответственно, исправленное стандартное откло- нение определяется по формуле:
n ri r 2
|
i 1 |
|
|
|
n 1 |
Пример
Определить стандартное отклонение доходности акции, ес- ли ее доходность за первый год составила 30%, второй – 35%, третий – 32%, четвертый – 29%, пятый – 34%.
Решение Осуществим расчеты по шагам.
ШАГ 1. Определяем среднюю доходность акции:
r 30 35 32 29 34 32% . 5
ШАГ 2. Определяем квадраты отклонений факти- ческих результатов за каждый год от средней доходно- сти:
30 32 2 4, 35 32 2 9, 32 32 2 0, 29 32 2 9, 34 32 2 4
ШАГ 3. Суммируем квадраты отклонений, делим сумму на количество лет минус единица и получаем исправленную дисперсию.
3 Несмещенной называют статистическую оценку некоторого па- раметра случайной величины, математическое ожидание которого равно оцениваемому параметру при любом объеме выборки.
350

2 4 9 0 9 4 6,5 4
ШАГ 4. Определяем исправленное стандартное от- клонение доходности акции:
6,5 2,55%
Рассматривая технику определения стандартного отклонения и цифровой пример, мы оперировали вре- менным периодом, равным году. На практике возникает задача определения стандартного отклонения для дру- гих временных периодов.
Если имеется значение стандартного отклонения за год, то для определения его за один день надо стан- дартное отклонение в расчете на год разделить на ко- рень квадратный из количества дней в году, а именно:
1  365 ,
365 ,
где: 1 – стандартное отклонение в расчете на один
день; – стандартное отклонение в расчете на год.
Так, стандартное отклонение доходности акции за один день в приведенном выше примере равно:
2,55365 0,133%
Следует, однако, иметь в виду, что торговля ценны- ми бумагами происходит не 365 дней в году. В году примерно 252 торговых дней, в течение которых и происходит изменение доходности акции. Поэтому для расчета стандартного отклонения за один день целесо- образно использовать 252 дня. Тогда стандартное от- клонение за день в примере составит:
2,55252 0,161%
351

Если мы определяем стандартное отклонение за не- который период на основе годичного стандартного от- клонения, то в общем виде формула имеет следующий вид:
t  252t ,
252t ,
где: t – стандартное отклонение за период t ;
t – период времени, для которого определяется стандартное отклонение;
– стандартное отклонение за год.
Пусть в нашем примере требуется определить стан- дартное отклонение доходности акции за 50 дней. В соответствии с формулой оно составит:
50 2,55 25250 1,136%
25250 1,136%
Если известно стандартное отклонение за один день, то определить его в расчете на год можно по формуле:
1  252
252
Соответственно стандартное отклонение за любой другой период времени t определяется по формуле:
t 1  t ,
t ,
где t – количество дней в периоде, за который рас- считывается стандартное отклонение.
Получить стандартное отклонение за год на основе его значения за некоторый период t можно с помо- щью формулы
t |
252 |
|
t |
||
|
Если стандартное отклонение за 50 дней составляет 1,136%, то в расчете на год оно равно:
352

1,136 |
252 |
2,55% |
|
50 |
|
На практике волатильность определяется на основе данных о ежедневной доходности акции. Доходность акции за один день определяется по формуле:
rti Sti Sti S1 ti 1 ,
где: rti – доходность акции за i день;
Sti – цена акции при закрытии i дня;
Sti 1 – цена акции при закрытии i 1дня.
Например, берут цену акции при закрытии вчера St0 и цену акции при закрытии сегодня St1 . Доходность
акции за первый день равна:
rt St1 St0
1 |
St0 |
|
Показатель rt1 является первым статистическим на-
блюдением. Далее берут цену акции при закрытии для дня t2 и определяют аналогичным образом доходность
акции за второй день и т.д. На основе полученных дан- ных о ежедневной доходности по формуле
|
|
n |
|
|
|
|
|
ri |
|
2 |
|
|
|
r |
|||
i 1 |
|
определяют волатильность в расчете |
|||
|
|
|
|
||
|
|
n 1 |
|
|
|
на один день. |
Затем по формуле 1 252 опреде- |
||||
ляют волатильность в расчете на год.
Удобство расчета стандартного отклонения на основе ежедневных данных состоит в том, что можно восполь- зоваться большим количеством наблюдений. В то же время, при определении волатильности на год на основе значения волатильности за день можно допустить
353

существенную погрешность. Она будет особенно вели- ка, если стандартное отклонение актива следует про- цессу «возвращение к среднему значению». Это означа- ет, что волатильность актива в долгосрочной перспективе испытывает колебания вокруг некоторого среднего значения, а не возрастает бесконечно про-
порционально величине  t , как это следует из фор-
t , как это следует из фор-
мулы t 1  t .
t .
На практике приемлемый результат получается, ес- ли рассчитывать стандартное отклонение для более длительных периодов на основе более коротких, ис- пользуя период времени до 10 дней. Так, определив волатильность в расчете на день, можно определить ее для периода в 10 дней, умножив полученную цифру на
значение  10 .
10 .
Когда инвестора интересует волатильность за более длительные периоды, можно взять прошлые статисти- ческие данные с требуемым интервалом. Например, инвестор определяет волатильность для одного месяца. Тогда необходимо взять наблюдения за предыдущие периоды времени по 30 дней. Причем, чтобы исклю- чить автокорреляцию4, следует использовать непересе- кающиеся временные периоды. Неудобство такого подхода при расчете волатильности для больших пе- риодов состоит в том, что приходится использовать наблюдения за несколько предыдущих лет.
Доходность акции является случайной величиной и поэтому может принимать различные значения. Если значения переменной изменяются во времени неопре- деленным образом, то говорят, что она следует стохас-
4 Автокорреляция – это термин, который говорит о том, что вели- чина переменной в следующий момент зависит от ее значения в предыдущий момент.
354
тическому, то есть вероятностному процессу. Значения переменной могут изменяться дискретно или непре- рывно. В первом случае величина переменной изменя- ется только на определенную (дискретную) величину, во втором – может принимать любые значения в рам- ках некоторого диапазона.
Значения одной переменной могут изменяться только в определенные моменты времени, другой – в любое время. Поэтому выделяют соответственно дис- кретный и непрерывный стохастические процессы.
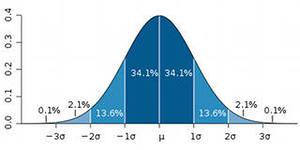
Доходность акции подчиняется нормальному рас- пределению. Нормальное распределение возникает в том случае, когда на случайную величину оказывает влияние множество факторов, каждый их которых не имеет определяющего значения. График кривой нор- мального распределения (график плотности вероятно- сти) случайной величины приведен на рис. 26.
Рис. 26. График кривой нормального распределения По оси абсцисс представлена область возможных значений случайной
величины Х , по оси ординат – плотность распределения вероятно- стей случайной величины Х . Плотность распределения f (x) явля-
ется одной из форм закона распределения случайной величины, но су- ществует только для непрерывных случайных величин.
График кривой нормального распределения сим- метричен относительно среднего значения случайной
355
величины, которое называют еще математическим ожиданием случайной величины. Сама случайная ве- личина может принимать любые отрицательные и по- ложительные значения. Правая и левая ветви графика асимптотически приближаются к оси абсцисс. Вся площадь, ограниченная кривой распределения и осью абсцисс, равна единице. Если нас интересует вероят- ность попадания случайной величины на какой-либо интервал оси абсцисс, то она будет равна площади фи- гуры, ограниченной сверху кривой распределения, сни- зу – осью абсцисс, по бокам – перпендикулярами, про- ходящими через концы интервала.
Нормальное распределение полностью определяется двумя характеристиками случайной величины – ее мате- матическим ожиданием и стандартным отклонением.
Стандартное отклонение характеризует степень рас- сеяния возможных значений случайной величины во- круг ее среднего значения. Кроме этого, оно говорит о вероятности того, что значение случайной переменной окажется в некотором интервале. Для нормально рас- пределенной случайной величины полезно запомнить так называемое «правило трех сигм». Оно говорит о том, что вероятность получить значение случайной переменной в диапазоне одного стандартного откло- нения от ее средней величины равно 68,3%, в диапазо- не двух стандартных отклонений – 95,4%, трех стан- дартных отклонений – 99,7%. Остается еще 0,3% вероятности того, что случайная величина примет лю- бое другое значение, выходящее за рамки отмеченных границ.
Проиллюстрируем данное правило на основе при- мера по расчету волатильности, который был приведен выше. Среднее значение или математическое ожидание доходности акции равнялось 32%, а стандартное от- клонение доходности в расчете на год – 2,55%.
356
Согласно «правилу трех сигм», инвестор вправе ожидать, что:
с вероятностью 68,3% доходность акции через год
будет располагаться в интервале от 32% 2,55% ,
то есть от 29,45% до 34,55%;
с вероятностью 95,4% этот интервал составит
32% 2 2,55% , то есть от 26,9% до 37,1%.;
с вероятностью 99,7% интервал возможной доход-
ности будет равен 32% 3 2,55% или от 24,35%
до 39,65%. Остаются еще 0,3% вероятности того, что акция принесет как гораздо более высокую, так и низкую доходность.
Стандартное отклонение является мерой риска из- менения доходности акции. Зная данную величину, инвестор может выбирать между более или менее рис- кованными бумагами. Например, имеются две акции A и B. Их средняя доходность одинакова и равна 30%, так как это просто средняя арифметическая их доходно- стей за определенный период времени. При этом стан- дартное отклонение в расчете на год акции A равно 10%, акции B – 15%. Из этого следует, что акция B рискованнее акции A. Исходя из правила трех сигм, инвестор с вероятностью 68,3% вправе ожидать полу- чения через год по бумаге A доходности в диапазоне от 20% до 40%, а по бумаге B – в диапазоне от 15% до 45%. По этой причине более консервативный вкладчик выберет бумагу A, а более склонный к риску – бумагу B.
10.4. НОВЫЕ МОДЕЛИ ОЦЕНКИ РИСКА
(ARCH, GARCH, EWMA)
В рамках традиционного подхода к определению риска акции значение ее дисперсии рассматривается во времени как неизменная величина. Данное свойство дисперсии называют гомоскедастичностью. Однако об-
357

щепризнанно, что ее величина подвержена изменениям. Свойство непостоянства дисперсии именуют термином гетероскедастичность.
Замечено: на финансовом рынке периоды низкой волатильности сменяются ее высокими периодами. В рамках каждого из этих периодов возникает эффект кла- стерности. Он говорит о том, что если сейчас на рынке наблюдается низкая волатильность, то наиболее веро- ятно, что она сохранится и в следующий момент. За высоким показателем волатильности, скорее всего, по- следует также высокое значение волатильности. Эф- фект кластерности был впервые обнаружен в 1963 г. Манделбротом.
Таким образом, если на рынке появилась информа- ция, которая вызвала рост или падение волатильности, то она будет сказываться на ней еще в течение некото- рого времени. Такое положение вещей говорит о том, что последние данные о динамике доходности актива имеют большее значение для прогнозирования теку- щего уровня дисперсии, чем более ранние. Поэтому при прогнозировании дисперсии последние статисти- ческие данные следует учитывать с большим удельным весом, чем более ранние.
10.4.1. Авторегрессионная условная гетероскедастичность (ARCH)
n ri r 2
При расчете дисперсии формула 2 i 1
n 1
обладает тем недостатком, что в ней не находит отра- жения временной порядок наблюдений, поскольку все они одинаковые удельные веса. Несколько трансфор- мируем данную формулу. Во-первых, в знаменателе вместо величины (n-1) возьмем n . Такое изменение не искажает существенно оценку дисперсии. Во-вторых,
358

придадим вес i |
каждому из наблюдений квадратов |
||||||||||||||||||||||||||
отклонений доходности. Тогда формула примет вид: |
|||||||||||||||||||||||||||
|
2 1 r1 |
|
2 |
2 r2 |
|
2 ... n rn |
|
2 |
|
||||||||||||||||||
|
r |
r |
r |
, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||||||||
|
Разделим все слагаемые на значение n : |
|
|
||||||||||||||||||||||||
2 |
1 |
r1 |
|
|
|
2 |
|
2 |
r2 |
|
2 ... |
n |
rn |
|
2 |
|
или |
||||||||||
r |
r |
r |
|
||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
n |
|
, |
||||||
2 |
1 |
r1 |
|
|
2 |
2 r2 |
|
2 ... n rn |
|
2 |
|
|
|||||||||||||||
r |
r |
r |
|
|
|||||||||||||||||||||||
где i ni – удельный вес каждого наблюдения квад-
рата отклонения доходности; общая сумма удельных весов равна единице.
За день доходность акции, как правило, изменяется не сильно. Поэтому ее средняя доходность мало отли- чается от нуля. Кроме того, дисперсия за день сущест- венно больше величины средней доходности. В итоге
среднюю доходность r можно считать равной нулю5. Тогда формула примет вид:
2 |
r 2 |
|
r 2 |
... |
r 2 |
или |
|
|
1 1 |
|
|
2 2 |
|
n n |
|
|
n |
|
|
|
|
|
|
2 |
i ri |
2 |
|
|
|
|
|
i 1
Можно предположить, что существует долгосроч- ная оценка дисперсии, и включить ее оценку в послед- нюю формулу. Получим:
n
2 gv i ri 2 ,
i 1
5 Такая корректировка ведет к некоторому смещению в сторону увеличения дисперсии, однако оно незначительно.
359
где: v – оценка долгосрочной дисперсии; g – ее удельный вес.
Обозначим gv через переменную w . Тогда
n
2 gv i ri 2 примет вид:
i 1
n
2 w i ri 2
i 1
Допустим, что мы рассчитываем дисперсию для дня n на основе данных p предшествующих дней, то есть
|
|
|
n |
|
p периодов, тогда формула |
2 |
w i ri |
2 примет |
|
следующий вид: |
|
|
i 1 |
|
|
|
|
|
|
p |
|
|
|
|
n 2 w i rn i |
2 , |
|
|
|
i 1
где n 2 – оценка дисперсии для n го дня. Приведенная формула представляет собой модель
ARCH p , название которой переводится как авторег-
рессионная условная гетероскедастичность. Она была разра-
ботана Р. Инглом в 1982 г. для отражения изменчивого характера дисперсии во времени. Как уже было отме- чено, модель оценивает дисперсию для n го дня на основе p наблюдений. Более ранним наблюдениям
придаются меньшие удельные веса.
p
В формуле n 2 w i rn i 2 значения rn i 2 мож-
i 1
но рассматривать как дисперсии доходности акции за каждый день наблюдений. Поэтому в рамках модели
ARCH p оценка дисперсии для следующего дня
(дня n) представляет собой сумму долгосрочной диспер- сии и дисперсий за последние p дней, взятых с соот-
ветствующими удельными весами, которые уменьша-
360
ются по мере удаления наблюдений от текущего дня. Поскольку в модель включено значение долгосрочной дисперсии, то она учитывает процесс «mean reversion» (возвращение к среднему значению).
10.4.2. Обобщенная авторегрессионная условная гетероскедастичность (GARCH)
Развитием модели ARCH является модель
GARCH −обобщенная авторегрессионная условная гетероскеда-
стичность. Она была предложена в 1986 г. Т. Борресле- вом. В дальнейшем в модель были внесены различные модификации. Первоначальная модель – это
GARCH 1,1 . Цифры в скобках говорят о том, что
прогноз дисперсии дается на основе последнего на- блюдения доходности актива и последней оценки дис- персии. Модель может строиться и на большем числе наблюдений. Тогда в общем виде ее название запишут
как GARCH p, q . В этом случае в модели использует- ся p последних значений доходности актива и q по-
следних оценок дисперсии. Наиболее популярной ос- |
|||||||
тается |
|
модель |
GARCH |
1,1 , |
представленная |
||
формулой: |
|
|
|
|
|||
|
2 |
|
gv r |
2 |
2 , |
|
|
|
n |
|
n 1 |
|
n 1 |
|
|
где: n |
2 – оценка дисперсии для n го дня, которая |
||||||
дается в конце дня n 1; |
|
|
|
||||
n 1 |
2 – оценка |
дисперсии |
доходности актива для |
||||
n 1 |
годня; |
|
|
|
|
||
rn 1 |
|
– доходность актива за n 1 й день; |
|||||
v – долгосрочная дисперсия;
g, , – удельные веса; сумма весов равняется еди- нице.
361

Как и в модели ARCH , в данной модели предпола- гается существование некоторого уровня долгосрочной дисперсии. Таким образом, она также учитывает про- цесс «mean reversion», что предполагает колебания дис- персии вокруг ее долгосрочного среднего значения.
Если обозначить gv w , то формула n 2 примет вид:
n 2 w rn 12 n 12
Пример
0,2; 0,7; g 0,1 . Оценка долгосрочного стан-
дартного отклонения доходности акции равна 1,6%, стандарт- ного отклонения для сегодняшнего дня – 1,2%, доходность бума- ги составила сегодня 1,5%. Определить оценку дисперсии и стандартного отклонения доходности акции для завтрашнего дня.
Решение
Определяем параметр w : w 0,1 1,62 0,256
Запишем уравнение модели:
|
n |
2 0,256 |
0,2r |
2 |
0,7 |
2 |
|
|
|
|
|
|
n 1 |
|
n 1 |
|
|
||
Учитывая, |
что rn 1 |
1,5%; n 1 |
1,2% , |
получаем |
|||||
оценку дисперсии для завтрашнего дня: |
|
||||||||
n |
2 0,256 |
0,2 1,52 0,7 1,22 |
1,714 |
|
|||||
Оценка |
|
стандартного |
отклонения |
равна |
|||||
1,714 1,3% |
|
|
|
|
|
|
|
||
Таким образом, прогноз волатильности для сле- дующего дня составляет 1,3%.
На основе параметра w модели из соотношения w gv можно определить значение долгосрочной
дисперсии. Так как g 1, то |
g 1 . То- |
гда долгосрочная дисперсия равна: |
|
362
|
|
v |
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
для n 1 |
||||
|
Запишем |
уравнение |
оценки |
дисперсии |
||||||||||||
дня: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
n 1 |
2 w r |
2 |
|
|
2 |
|
|
|
|
|||||
|
|
|
|
|
n 2 |
|
|
|
n 2 |
|
|
|
|
|||
|
Подставим |
|
|
его |
|
|
в |
|
уравнение |
|||||||
|
2 |
w r |
2 |
|
2 |
: |
|
|
|
|
|
|||||
|
n |
|
|
|
n 1 |
|
|
n 1 |
|
|
|
|
|
|
||
|
n 2 w rn 12 w rn 2 2 n 2 2 |
|
||||||||||||||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
2 |
|
w w r |
2 |
r |
2 |
2 |
2 |
|
||||||
|
|
|
n |
|
|
|
|
n 1 |
|
n 2 |
|
n 2 |
|
|||
|
Аналогично подставим в последнее уравнение |
|||||||||||||||
оценку дисперсии для n 2 дня: |
|
|
|
|
||||||||||||
n 2 |
w w rn 12 rn 2 2 2 w rn 3 2 n 3 2 w 1 2 |
|||||||||||||||
rn 12 rn 2 2 2 rn 3 2 |
3 n 3 2 |
|
|
|
|
|||||||||||
|
Из последнего выражения видно, что вес параметра |
|||||||||||||||
r |
|
составляет i 1 , то есть веса убывают по экспонен- |
||||||||||||||
n i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
те со скоростью . Таким образом, параметр пока-
зывает уровень влияния, которое оказывают значения r за определенный день на оценку дисперсии в моде-
ли. Чтобы воспользоваться моделью GARCH 1,1 , ин-
вестор должен оценить ее параметры. Это можно сде- лать с помощью метода наибольшего правдоподобия.
10.4.3. Экспоненциально взвешенная
скользящая средняя (EWMA)
Другой моделью, учитывающей нестабильный характер дисперсии, является модель экспоненциально
взвешенной скользящей средней – EWMA. Формула модели имеет следующий вид:
n 2 n 12 1 rn 12 ,
363
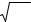
где: n |
2 – оценка дисперсии для n годня, которая |
дается в конце дня n 1; |
|
n 1 |
2 – оценка дисперсии для n 1 го дня; |
rn 1 |
– доходность актива за n 1 день; |
– удельный вес.
Банк Дж. П. Морган для определения текущей еже- дневной дисперсии принял значение равным 0,94.
Пример
Оценка стандартного отклонения для сегодняшнего дня рав- на 2%, доходность акции за день составила 3%. Оценить дис- персию и волатильность для завтрашнего дня.
Решение
Сегодняшний день – это день n 1. Требуется оце- нить дисперсию завтрашнего дня, то есть дня n . При-
нимая равной 0,94, получим оценку дисперсии:
n |
2 0,94 22 1 0,94 32 4,3 |
|
|
|
|
|
||
Оценка волатильности равна |
4,3 2,07% |
|
|
|
||||
Как видно из формулы |
n |
2 |
2 |
1 |
r |
2 |
, |
|
|
|
|
n 1 |
|
n 1 |
|
||
для оценки дисперсии доходности акции для следую- щего дня необходимо знать только два параметра: оценку дисперсии и доходность актива за текущий день.
Остановимся подробнее на роли параметра в модели. Его можно рассматривать двояко. Во-первых, он определяет удельный вес, с которым последнее зна- чение доходности включается в модель. Конкретно
удельный вес представляет собой величину 1 . По-
этому, чем больше , тем в меньшей степени послед- няя доходность влияет на оценку дисперсии, и наобо-
рот. Во-вторых, определяет скорость возвращения дисперсии к своему предыдущему уровню после резко-
го изменения доходности. Чем меньше величина ,
364
тем быстрее дисперсия вернется к предыдущему уров- ню после сильного изменения доходности. Формула
определения n 2 предполагает, что мы можем предста-
вить оценку дисперсии как экспоненциально взвешен- ную скользящую среднюю. Оценка дисперсии для n 1 го дня равна:
n 12 n 2 2 1 rn 2 2 ,
где: σ n 2 2оценка– дисперсии для n −2 −го дня, которая
дается в конце дня n −3;
rn 2 – доходность актива за n 2 день. Подставив формулу n 12 n 2 2 1 rn 2 2 в формулу опре- деления n 2 , получим:
n 2 n 2 2 1 rn 2 2 1 rn 12 2 n 2 2 1 rn 12 rn 2 2
Подставим в последнюю формулу оценку диспер- сии для n 2 го дня:
n 2 2 n 3 2 1 rn 3 2 1 rn 12 rn 2 2
или
n 2 3 n 3 2 1 rn 12 rn 2 2 2 rn 3 2
Взяв p периодов наблюдения, получим:
|
|
2 p |
n p |
2 1 |
p |
i 1r |
2 |
|
|
|||||
|
|
n |
|
|
|
|
|
|
|
n i |
|
|
||
|
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
Если |
взять |
большое |
|
количество наблюдений |
|||||||||
p , то первое слагаемое p n p |
2 |
будет стремиться |
||||||||||||
к нулю, и им |
можно |
пренебречь. |
Тогда формула |
|||||||||||
|
2 p |
2 |
1 |
|
p |
i 1r |
2 |
примет вид: |
||||||
|
n |
|
n p |
|
|
|
|
|
n i |
|
|
|
||
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
2 1 |
|
i 1r |
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||||||
|
|
n |
|
|
|
n i |
|
|
|
|
|
|
||
i 1
365
В приведенной формуле удельный вес величины r 2 убывает со скоростью 1 i 1 . Таким образом, по
мере движения назад, к более ранним наблюдениям значений доходности, их веса быстро приближаются к нулю, хотя и не обращаются в ноль. Поэтому при зна- чении 0,94 оценку дисперсии, согласно последней
формуле, можно сделать на основе 50 наблюдений. Использование такого временного интервала уже дает хороший результат, так как доходность за первый день наблюдений будет учтена в формуле с удельным весом:
1 0,94 0,9449 0,0029 .
Даже если использовать только 30 наблюдений, по- грешность будет незначительная, поскольку удельный вес 30-го наблюдения составит порядка 0,01.
Обозначив 1 p 1 , где – требуемый уро-
вень удельного веса для первого наблюдения. Тогда количество наблюдений для требуемого уровня точно- сти расчета можно определить по формуле:
|
ln |
|
|
||
p |
1 |
1. |
|||
|
|||||
ln
Если сравнить модели GARCH 1,1 и EWMA, то можно заметить, что при значении w 0 GARCH пре- образуется в EWMA. Поскольку GARCH 1,1 включает долгосрочную дисперсию, это означает, что она учи-
тывает эффект «mean reversion», в то время как EWMA нет. Как было отмечено выше, для пользования моде-
лью GARCH необходимо оценить удельные веса вхо- дящих в нее слагаемых. Если в этом случае удельный вес долгосрочной дисперсии окажется отрицательным,
то лучше использовать модель EWMA.
366
