
- •6) Проведем укрупнение групп аналитической группировки, образовав 3 типические группы.
- •Задание 2.
- •Задание 3.
- •Решение.
- •Задание 4.
- •По характеру фактических уровней, принимаем гипотезу о существовании прямолинейного тренда (динамика доли инновационных товаров и услуг характеризуется прямой линией).
- •Глава 3. Статистико-экономический анализ научно-технического прогресса в экономике с использованием одного из методов статистики.
- •3.1 Статистическое наблюдение.
- •Решение.
- •2. Построим ранжированный ряд регионов по доле инновационных товаров, работ и услуг в общем объеме отгруженных товаров.
- •3)Построим интервальный ряд распределения.
- •4)По данным интервального ряда рассчитаем:
РАСЧЕТНАЯ ЧАСТЬ.
Задание 1.
На основе данных таблицы 1 выполнить задания:
Таблица 2.1 – Статистическая информация о результатах научной и производственной деятельности организаций
|
№ |
Объем инновационных товаров, работ, услуг, млн. руб. |
Объем отгруженных товаров и услуг, млрд. руб. |
Число организаций, выполнявших научные разработки, ед. |
Численность персонала, занятого научными исследованиями и разработками, чел. |
Численность исследователей с учеными степенями, чел. |
|
1 |
9391,6 |
361,2 |
16 |
1189 |
309 |
|
2 |
4434,4 |
94,3 |
17 |
790 |
50 |
|
3 |
4958 |
215,6 |
25 |
4871 |
286 |
|
4 |
13431,8 |
189,2 |
58 |
13184 |
919 |
|
5 |
2479,9 |
70,9 |
21 |
749 |
259 |
|
6 |
7190,6 |
256,8 |
37 |
10091 |
940 |
|
7 |
2159,2 |
69,7 |
6 |
116 |
21 |
|
8 |
1007,7 |
168 |
15 |
2944 |
144 |
|
9 |
31511,2 |
321,5 |
10 |
323 |
100 |
|
10 |
90231,3 |
1114 |
257 |
84574 |
8600 |
|
11 |
5868,9 |
59,3 |
14 |
797 |
171 |
|
12 |
4497,5 |
136,3 |
16 |
2373 |
174 |
|
13 |
2367 |
10,3 |
17 |
873 |
64 |
|
14 |
2104,6 |
58,5 |
22 |
1665 |
179 |
|
15 |
14948,3 |
162,5 |
28 |
4851 |
462 |
|
16 |
8395,6 |
246,9 |
21 |
4992 |
178 |
|
17 |
21237 |
175,5 |
29 |
6187 |
884 |
|
18 |
1058,7 |
81,4 |
16 |
934 |
314 |
|
19 |
8830,3 |
275,9 |
23 |
1806 |
435 |
|
20 |
1024,5 |
256,1 |
33 |
1148 |
151 |
|
21 |
5570,1 |
348,1 |
17 |
482 |
72 |
|
22 |
222,6 |
222,6 |
11 |
1859 |
116 |
|
23 |
9959,2 |
415 |
14 |
6477 |
579 |
|
24 |
792,5 |
158,5 |
25 |
2097 |
498 |
1. Рассчитайте: долю инновационных товаров, работ и услуг в общем объеме отгруженных товаров; объем инновационных товаров на 1 работника, занятого научными исследованиями и разработками; долю исследователей с учеными степенями в общей численности персонала, занятого научными исследованиями и разработками: численность персонала, занятого научными исследованиями и разработками в среднем на 1 научную организацию.
Решение.
Доля инновационных товаров, работ и услуг в общем объеме отгруженных товаров рассчитывается как отношение объема инновационных товаров, работ и услуг (млн. руб.) к объему отгруженных товаров и услуг (млрд. руб.).
Объем инновационных товаров на 1 работника, занятого научными исследованиями и разработками рассчитывается как отношение объема инновационных товаров, работ и услуг (млн. руб.) к численности персонала, занятого научными исследованиями и разработками (чел.).
Доля исследователей с учеными степенями в общей численности персонала, занятого научными исследованиями и разработками рассчитывается как отношение численности исследователей с учеными степенями (чел.) к общей численности персонала, занятого научными исследованиями и разработками (чел.).
Численность персонала, занятого научными исследованиями и разработками в среднем на 1 научную организацию рассчитывается как отношение численности персонала, занятого научными исследованиями и разработками (чел.) к числу организаций, выполнявших научные разработки (ед.).
Результаты расчетов приведены в Таблице 2.2:
Таблица 2.2 Результаты расчетов по первому пункту первого задания.
|
№ |
Доля инновационных товаров, работ и услуг в общем объеме отгруженных товаров |
Объем инновационных товаров на 1 работника, занятого научными исследованиями и разработками |
Доля исследователей с учеными степенями в общей численности персонала, занятого научными исследованиями и разработками |
Численность персонала, занятого научными исследованиями и разработками в среднем на 1 научную организацию |
|
1 |
26,001 |
7,899 |
0,260 |
74,313 |
|
2 |
47,024 |
5,613 |
0,063 |
46,471 |
|
3 |
22,996 |
1,018 |
0,059 |
194,840 |
|
4 |
70,993 |
1,019 |
0,070 |
227,310 |
|
5 |
34,977 |
3,311 |
0,346 |
35,667 |
|
6 |
28,001 |
0,713 |
0,093 |
272,730 |
|
7 |
30,978 |
18,614 |
0,181 |
19,333 |
|
8 |
5,998 |
0,342 |
0,049 |
196,267 |
|
9 |
98,013 |
97,558 |
0,310 |
32,300 |
|
10 |
80,998 |
1,067 |
0,102 |
329,082 |
|
11 |
98,970 |
7,364 |
0,215 |
56,929 |
|
12 |
32,997 |
1,895 |
0,073 |
148,313 |
|
13 |
229,806 |
2,711 |
0,073 |
51,353 |
|
14 |
35,976 |
1,264 |
0,108 |
75,682 |
|
15 |
91,990 |
3,081 |
0,095 |
173,250 |
|
16 |
34,004 |
1,682 |
0,036 |
237,714 |
|
17 |
121,009 |
3,433 |
0,143 |
213,345 |
|
18 |
13,006 |
1,134 |
0,336 |
58,375 |
|
19 |
32,005 |
4,889 |
0,241 |
78,522 |
|
20 |
4,000 |
0,892 |
0,132 |
34,788 |
|
21 |
16,001 |
11,556 |
0,149 |
28,353 |
|
22 |
1,000 |
0,120 |
0,062 |
169,000 |
|
23 |
23,998 |
1,538 |
0,089 |
462,643 |
|
24 |
5,000 |
0,378 |
0,233 |
83,880 |
2. Постройте ранжированный ряд регионов по доле исследователей с учеными степенями в общей численности персонала, занятого научными исследованиями и разработками, а затем образуйте интервальный ряд распределения из пяти групп с равными интервалами.
Решение.
Ранжированный ряд по доле исследователей с учеными степенями в общей численности персонала, занятого научными исследованиями и разработками представляет собой таблицу, в которой организации расставлены в порядке возрастания признака (Таблица 2.3).
Таблица 2.3. Ранжированный ряд по доле исследователей с учеными степенями в общей численности персонала.
|
№ |
Доля исследователей с учеными степенями в общей численности персонала, занятого научными исследованиями и разработками |
№ |
Доля исследователей с учеными степенями в общей численности персонала, занятого научными исследованиями и разработками |
|
16 |
0,036 |
14 |
0,108 |
|
8 |
0,049 |
20 |
0,132 |
|
3 |
0,059 |
17 |
0,143 |
|
22 |
0,062 |
21 |
0,149 |
|
2 |
0,063 |
7 |
0,181 |
|
4 |
0,070 |
11 |
0,215 |
|
12 |
0,073 |
24 |
0,233 |
|
13 |
0,073 |
19 |
0,241 |
|
23 |
0,089 |
1 |
0,260 |
|
6 |
0,093 |
9 |
0,310 |
|
15 |
0,095 |
19 |
0,336 |
|
10 |
0,102 |
5 |
0,346 |
Путем построения ранжированного ряда распределения, таблица 2.3., получаем минимальное значение, равное 0,036 и максимальное значение, равное 0,346. Величину интервала можно вычислить по формуле
 (1.1)
(1.1)
Где h - величина интервала, xmax - максимальное значение признака, xmin – минимальное значение признака, количество требуемых групп, n – количество требуемых групп в интервальном ряду (в данном случае 5 групп).

Таблица 2.4. Интервальный ряд по доле исследователей с учеными степенями в общей численности персонала.
|
№ группы |
Интервал |
Кол-во регионов в группе |
№ региона |
Доля исследователей с учеными степенями в общей численности персонала |
|
1 |
0,036 – 0,098 |
11 |
16 |
0,036 |
|
8 |
0,049 |
|||
|
3 |
0,059 |
|||
|
22 |
0,062 |
|||
|
2 |
0,063 |
|||
|
4 |
0,070 |
|||
|
12 |
0,073 |
|||
|
13 |
0,073 |
|||
|
23 |
0,089 |
|||
|
6 |
0,093 |
|||
|
15 |
0,095 |
|||
|
2 |
0,098 – 0,16 |
2 |
10 |
0,102 |
|
14 |
0,108 |
|||
|
3 |
0,16 – 0,222 |
5 |
20 |
0,132 |
|
17 |
0,143 |
|||
|
21 |
0,149 |
|||
|
7 |
0,181 |
|||
|
11 |
0,215 |
|||
|
4 |
0,222 – 0,284 |
3 |
24 |
0,233 |
|
19 |
0,241 |
|||
|
1 |
0,260 |
|||
|
5 |
0,284 – 0,346 |
3 |
9 |
0,310 |
|
19 |
0,336 |
|||
|
5 |
0,346 |
3. Постройте графики ранжированного и интервального рядов распределения;

Рис. 1 График ранжированного ряда распределения регионов по доле исследователей с учеными степенями в общей численности персонала.

Рис. 2 График интервального распределения регионов по доле исследователей с учеными степенями в общей численности персонала.
Интервальный ряд распределения регионов РФ по доле исследователей с учеными степенями в общей численности персонала показывает, что в совокупности преобладает доля от 0,036 до 0,098.
4. По данным интервального ряда распределения рассчитайте: размах вариации, среднее квадратичное отклонение, коэффициент вариации, моду и медиану.
Решение.
Размах
вариации:
 (1.2)
(1.2)

Размах вариации равен 0,31.
Размах вариации имеет большое значение, что говорит о том, что величины отношений сильно отличаются друг от друга.
Наиболее
совершенной характеристикой вариации
является среднее квадратическое
отклонение, которое называют стандартом
(или стандартным отклонение). Среднее
квадратическое отклонение (![]() )
равно квадратному корню из среднего
квадрата отклонений отдельных значений
признака от средней
арифметической:
)
равно квадратному корню из среднего
квадрата отклонений отдельных значений
признака от средней
арифметической:
σ
=
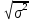 (1.3)
(1.3)
где
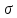 -
среднее квадратическое отклонение.
-
среднее квадратическое отклонение.
 -
дисперсия.
-
дисперсия.
Таблица 2.5 Расчетная таблица интервального ряда распределения регионов.
|
№ |
Группы по доле исследователей с учеными степенями в общей численности персонала |
Число регионов в группе |
x' |
x'f |
|
|
|
|
Xi |
fi |
||||
|
1 |
0,036 – 0,098 |
11 |
0,067 |
0,737 |
0,083 |
0,00689 |
|
2 |
0,098 – 0,16 |
2 |
0,129 |
0,258 |
0,021 |
0,00044 |
|
3 |
0,16 – 0,222 |
5 |
0,191 |
0,955 |
0,041 |
0,00168 |
|
4 |
0,222 – 0,284 |
3 |
0,253 |
0,759 |
0,103 |
0,01061 |
|
5 |
0,284 – 0,346 |
3 |
0,315 |
0,945 |
0,165 |
0,02723 |
|
|
Итого |
24 |
|
3,654 |
0,413 |
0,04685 |
Показатель дисперсии:
 ,
(1.4)
,
(1.4)
где
 – среднее значение x
– среднее значение x
 =
=
 (1.5)
(1.5)
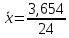 =
0,15
=
0,15
Отсюда следует, что:
 =
=
 = 0,00195
= 0,00195
Соответственно:
 =
=
 = 0,04416
= 0,04416
Среднее квадратическое отклонение равно 0,044
Коэффициент вариации:
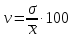 (1.6)
(1.6)

Поскольку коэффициент вариации меньше 33 %, то совокупность по данному показателю однородна.
Мода и медиана:
Мода для интервального ряда распределения:
 (1.7),
где
(1.7),
где
 – нижняя
граница модального интервала;
– нижняя
граница модального интервала;
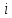 – шаг
модального интервала;
– шаг
модального интервала;
 – локальная
частота модально интервала;
– локальная
частота модально интервала;
 – локальная
частота интервала, предшествующего
модальному;
– локальная
частота интервала, предшествующего
модальному;
 – локальная
частота интервала, следующего за
модальным.
– локальная
частота интервала, следующего за
модальным.
Модальным будет интервал 0,036 – 0,098, т.к. у него наибольшая частота.
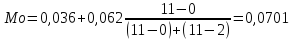
Найдя моду можно сделать вывод, что чаще всего в этой совокупности встречаются регионы со средней долей исследователей с учеными степенями в общей численности персонала равной 0,0701.
Медианным интервалом в интервальном ряду распределения будет являться интервал второй группы, т. к его накопленная частота превышает половину всего объема совокупности.
Для определения медианы произведем дополнительные расчеты, которые представлены в таблице 2.6.
Таблица 2.6. Дополнительные расчеты для определения медианного интервала.
|
Группы по количеству внесенных минеральных удобрений кг на га |
Число организаций (fi) |
Сумма f |
|
0,036 – 0,098 |
11 |
11 |
|
0,098 – 0,16 |
2 |
13 |
|
0,16 – 0,222 |
5 |
18 |
|
0,222 – 0,284 |
3 |
21 |
|
0,284 – 0,346 |
3 |
24 |
Формула для расчета медианы:

X0 – нижняя граница интервала, в котором находится медиана;
h – размах интервала;
fme-1 – накопленная частота в интервале, предшествующем медианному;
fme – частота в медианном интервале.
 =
0,129
=
0,129
Медиана равна 0,129, т.е. в половине регионов доля исследователей с учеными степенями в общей численности персонала меньше чем 0,129, а в другой половине – больше.
5. Полученные группы по факторному признаку дополните расчетами доли инновационных товаров, работ и услуг в общем объеме отгруженных товаров; объема инновационных товаров на 1 работника, занятого научными исследованиями и разработками; численность персонала, занятого научными исследованиями и разработками, в среднем на 1 научную организацию и установите наличие и характер корреляционной связи между факторным и результативным признаками.
Решение.
С целью установления наличия и характера корреляционной связи между группировочным и расчетными признаками проведем аналитическую группировку (табл. 2.7).
Таблица 2.7 Аналитическая группировка регионов РФ.
|
Группы по доле исследователей с учеными степенями в общей численности персонала |
Число организаций |
Доля инновационных товаров, работ и услуг в общем объеме отгруженных товаров |
Объем инновационных товаров на 1 работника, занятого научными исследованиями и разработками |
Численность персонала, занятого научными исследованиями и разработками в среднем на 1 научную организацию |
|
0,036 – 0,098 |
11 |
53,528 |
1,794 |
198,172 |
|
0,098 – 0,16 |
2 |
58,487 |
1,166 |
202,382 |
|
0,16 – 0,222 |
5 |
54,192 |
8,372 |
70,550 |
|
0,222 – 0,284 |
3 |
21,002 |
4,389 |
78,905 |
|
0,284 – 0,346 |
3 |
54,998 |
35,253 |
48,830 |
|
Всего |
24 |
|
|
|
6) Проведем укрупнение групп аналитической группировки, образовав 3 типические группы.
Аналитические группировки используются для исследования наличия зависимости между изучаемыми явлениями. Для этого следует данные сгруппировать по одному из признаков, вычислить в каждой группе среднее значение второго признака, а затем сопоставить изменения изучаемых признаков. Если с увеличением или уменьшением группировочного признака увеличиваются значения второго признака, то связь (прямая или обратная) между ними существует.
Таблица 2.7 -Типические группы
|
интервал |
fl |
Доля инновационных товаров, работ и услуг в общем объеме отгруженных товаров |
Объем инновационных товаров на 1 работника, занятого научными исследованиями и разработками |
Численность персонала, занятого научными исследованиями и разработками в среднем на 1 научную организацию |
|
0,036 – 0,16 |
11 2 |
53,528 58,487 |
1,794 1,166 |
198,172 202,382 |
|
0,16 - 0,284 |
5 3 |
54,192 21,002 |
8,372 4,389 |
70,550 78,905 |
|
0,284 - 0,346 |
3 |
54,998 |
35,253 |
48,830 |
От 0,036-0,16 – низшая группа
0,16-0,284 – средняя группа
0,284-0,346 – высшая группа.
Анализ данных таблицы показывает что:
- Между факторами существует гиперболическая связь, т.к. за увеличением значений переменных следует их уменьшение, затем снова увеличение и т.д.
- Доля инновационных товаров, работ и услуг в общем объеме отгруженных товаров уменьшается ко второй группе, затем увеличивается в третьей.
- Объем инновационных товаров на 1 работника, занятого научными исследованиями и разработками увеличивается от первой группы к третьей.
- Численность персонала, занятого научными исследованиями и разработками в среднем на 1 научную организацию уменьшается от первой группы к третьей.
Задание 2.
Имеются следующие данные (Таблица 2.8)
Таблица 2.8 – Объем инновацион6ных товаров, работ и услуг по организациям, выполняющим научные разработки
|
Регион |
Объем инновационных товаров, работ, услуг, тыс. руб. |
Численность организаций, выполнявших научные разработки |
|||
|
Базисный период |
Отчетный период |
Базисный период |
Отчетный период |
||
|
|
|
|
|
||
|
А |
32978.9 |
10437.5 |
1189 |
1185 |
|
|
Б |
10155.1 |
9913.6 |
2010 |
1352 |
|
|
В |
5110.4 |
4665.0 |
7075 |
6638 |
|
Определить: 1) уровень и динамику объема производства инновационных товаров и услуг на 1 предприятие по каждому региону; 2) по трем регионам вместе: а) индекс производства переменного состава; б) индекс производства постоянного (фиксированного состава); в) агрегатный индекс влияния структурных сдвигов за счет изменения числа организаций; г) абсолютное изменение объема инновационных товаров, работ и услуг в отчетном периоде по сравнению с базисным в результате изменения каждого из факторов.
Решение.
Таблица 2.9 Расчетная таблица индексов.
|
Регион |
Численность организаций, выполняющих научные разработки |
Объем инновационных товаров, работ, услуг, тыс. руб. |
Объем производства инновационных товаров и услуг на 1 предприятие |
Индексы |
||||||
|
Базисный период, q0 |
Отчетный период, q1 |
Базисный период, p0q0 |
Отчетный период, p1q1 |
Базисный период, p0 |
Отчетный период, p1 |
|
||||
|
А |
1189 |
1185 |
32978,9 |
10437,5 |
27,74 |
8,81 |
0,32 |
|||
|
Б |
2010 |
1352 |
10155,1 |
9913,6 |
5,05 |
7,33 |
1,45 |
|||
|
В |
7075 |
6638 |
5110,4 |
4665,0 |
0,72 |
0,70 |
0,97 |
|||
|
Сумма |
10274 |
9175 |
48244,4 |
25016,1 |
33,51 |
16,84 |
|
|||
1) Объем производства инновационных товаров и услуг на 1 предприятие составил:
Регион А:
В базисном периоде
p0 = ( p0 *q0)/ q0 = 32978,9/1189 = 27,74
Регион Б:
p0 = ( p0 *q0)/ q0 = 10155,1/2010 = 5,05
Регион В:
p0 = ( p0 *q0)/ q0 = 5110,4/7075 = 0,72
В текущем периоде
Регион А:
p1 = ( p1 *q1)/ q1 = 10437,5/1185 = 8,81
Регион Б:
p1 = ( p1 *q1)/ q1 = 9913,6/1352 = 7,33
Регион В:
p1 = ( p1 * q1)/ q1 = 4665,0/6638 = 0,70
Индекс объема производства на 1 предприятие региона А составил:
ip = p1 / p0 = 8,81 / 27,74 = 0,32
Регион Б:
ip = p1 / p0 = 7,33 / 5,05 = 1,45
Регион В:
ip = p1 / p0 = 0,7 / 0,72 = 0,97
Общий индекс объема производства на 1 предприятие (индекс переменного состава)

Ip = (25016,1/9175) / (48244,4 / 10274) = 2,73/4,7 = 0,58
P0 ср = 48244,4/10274 = 4,7
2) По трем регионам:
а) Найдем индекс производства переменного состава:
iпер = 25016,1/48244,4 = 0,52
б) Найдем индекс фиксированного состава:

iфикс = 25016,1/(27,74*1185+5,05*1352+0,72*6638) = 25016,1/44478,86 = = 0,56
в) Индекс влияния структурных сдвигов:
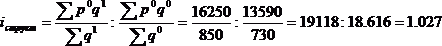
iструкт = (44478,86/9175)/(48244,4/10274) = 4,85/4,7 = 1,03
г) Абсолютное изменение объема инновационных товаров, работ и услуг:
Вычислим структуру организаций, выполняющих научные разработки в базисном и отчетном периоде.
d10 = 1189/10274 = 0,12
d20 = 2010/10274 = 0,2
d30 = 7075/10274 = 0,69
d11 = 1185/9175 = 0,13
d21 = 1352/9175 = 0,15
d31 = 6638/9175 = 0,72
Прирост объема инновационных товаров, работ и услуг от изменения объема инновационных товаров и услуг на 1 предприятие:
![]()
∆pqd(p) = (0,13*(8,81 – 27,74) + 0,15*(7,33 – 5,05) + 0,72*(0,70 – 0,72))*9175 = -19634,5
Прирост объема инновационных товаров, работ и услуг от изменения структуры составил:
![]()
∆pqd(d) = ((27,74*0,13+5,05*0,15+0,72*0,72) - (27,74*0,12+5,05*0,2+0,72*0,69))*9175 = (4,89 – 4,84)*9175 = 458,75
Прирост объема инновационных товаров, работ и услуг от изменения численности организаций:
![]()
∆pqd(q) = (4,84*(-1099)) = - 5319,16
Общий прирост составил
25016,1 – 48244,4 = -23228,3
Прирост за счет отдельных факторов составил:
- 19634,5 + 458,75 – 5319,16 ≈ -24494,91
Таким образом можно сделать выводы, что численность организаций, выполняющих научные разработки, объем инновационных товаров, работ, услуг , объем производства инновационных товаров и услуг на 1 предприятие в регионе А в отчетном периоде уменьшились по сравнению с базисным; численность организаций, выполняющих научные разработки, объем инновационных товаров, работ, услуг в регионе Б в отчетном периоде уменьшились по сравнению с базисным, а объем производства инновационных товаров и услуг на 1 предприятие в отчетном периоде увеличился; численность организаций, выполняющих научные разработки, объем инновационных товаров, работ, услуг , объем производства инновационных товаров и услуг на 1 предприятие в регионе В в отчетном периоде уменьшились по сравнению с базисным.


 2
2


