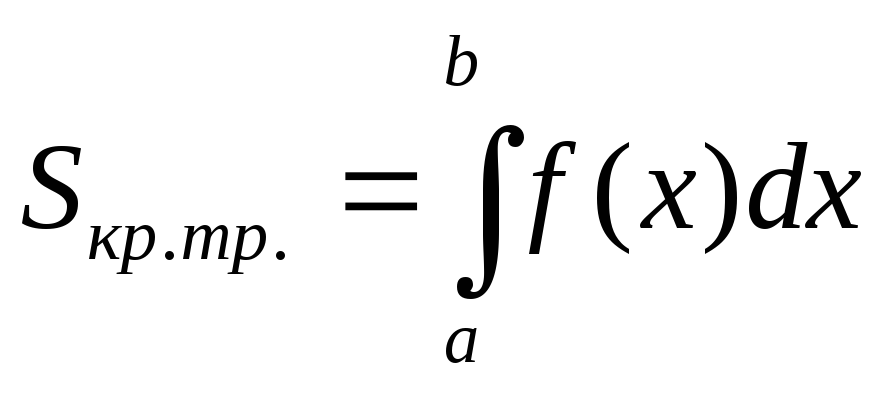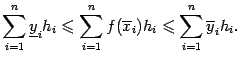опред.интегр

Определенный интеграл.

1. Понятие интегральной суммы.

2. Понятие определенного интеграла.

3. свойства определенного интеграла.

4. Методы интегрирования:

   0. 4.1. метод замены переменной;

   0. 4.2. метод интегрирования по частям.

5. Приложение определенного интеграла:

   0. 5.1. площадь криволинейной трапеции;

   1. 5.2. длина дуги плоской кривой;

   2. 5.3. объём тела;

   3. 5.4. поверхность тела

1.

Рассмотрим задачу о нахождении площади плоской области , ограниченной на координатной плоскости отрезком оси , графиком непрерывной функции , заданной на отрезке , и двумя отрезками вертикальных прямых и , соединяющими точки оси с точками графика

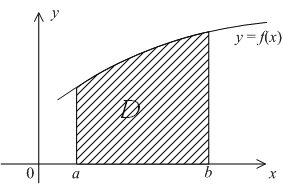
Эту фигуру мы будем в общем случае называть криволинейной трапецией (считая параллельные вертикальные отрезки и её основаниями).

Сначала попробуем найти значение искомой площади приближённо. Для этого разделим область на узкие вертикальные полоски , проведя вертикальные линии ; при этом мы будем считать, что Тогда область лежит между прямыми и , где . Обозначим длины отрезков между такими прямыми через : . Очевидно, что площадь области лежит в пределах от до , где и (см. рис.), и примерно равна , где  -- произвольная точка отрезка .

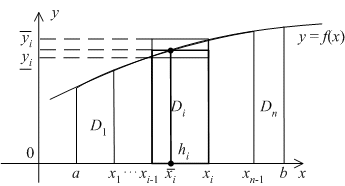
Легко видеть также, что при любом выборе точек мы получаем

Тогда искомая площадь 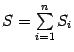приблизительно равна сумме величин :

и лежит между суммой площадей и :

Из неравенства (3.1) следует также, что при любом выборе точек получаем

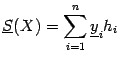Рассматривая на каждом из отрезков разбиения значения и (в случае непрерывной функции они совпадают с и , которые мы рассматривали выше), мы можем дать для разбиения определение нижней интегральной суммы: и верхней интегральной суммы:

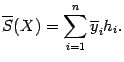
2.

Обозначим длину наибольшего из отрезков разбиения через max ∆х_i, где i=1,2,…n

Пусть предел интегральной суммы Σ f(C_i)∆x_i при стремлении max ∆х_i к нулю существует, конечен и не зависит от способа разбиения отрезка [

n

a, в] на части и от выбора точек Тогда этот предел называется определенным интегралом от функции у = f(х) на [а, в] и обозначается , т

i=1

.е =lim Σ f(С_i)∆x_i при max ∆x_i →0.

Число а называется нижним пределом, b – верхним пределом, f(x) – подынтегральной функцией, f(x)dx – подынтегральным выражением.

Заодно, кроме общего определения определённого интеграла, мы получили определение площади криволинейной трапеции, лежащей под графиком функции , как такого же предела интегральных сумм: 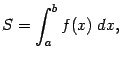если функция непрерывна на и при всех .

Из определения определённого интеграла отнюдь не следует, что любая функция интегрируема на любом интервале. Можно подобрать такие функции, для которых определённый интеграл не существует, то есть для которых интегральная сумма не стремится к определённому пределу. Существование определённого интеграла от функции, заданной на интервале [а,в], обеспечивает непрерывность этой функции на [а,в], поэтому непрерывность функции на [а,в] является достаточным условием её интегрируемости на этом интервале, то есть,

Теорема. Если функция f(х) непрерывна на замкнутом интервале [а,в], то она интегрируема на этом интервале, то есть имеет определённый интеграл .

Иногда на практике приходится интегрировать и разрывные функции. Приведём несколько более широкое достаточное условие существования интеграла.

Теорема . Если на интервале [а,в] функция ограничена и имеет лишь конечное число точек разрыва, то она интегрируема на [а,в].

3.

1⁰ . Значение определенного интеграла не зависит от обозначения переменной интегрирования, т.е. = = и т.д.

2⁰. есть число.

3⁰. Если а = b, то, по определению, полагают

4⁰. = - , а<b

5⁰. Постоянный множитель можно выносить за знак интеграла: = k , где k – const.

Доказательство: По определению: kf(х)dх=lim [k f(x₁)∆х₁+k f(x₂)∆х₂+…+k f(x_n)∆х_n]=

= lim kf(x_i) ∆х_i. Но так как, согласно одному из свойств предела, lim kf(x_i)∆х_i.=

= k lim f(x_i) ∆х_i, и так как, по определению, lim k f(x_i)∆х_i.=, то = =k lim f(x_i) ∆х_i=k.

6⁰. Определённый интеграл от алгебраической суммы нескольких непрерывных функций равен алгебраической сумме определённых интегралов от этих функций.

Доказательство: Докажем, например, что [f₁(х)+f₂(х)– f₃(х)]dх = f₁(х)dх +

+f₂(х)dх – f₃(х)dх в самом деле имеем: [f₁(х)+f₂(х)–f₃(х)]dх=lim ( f(x₁)∆х₁+ +f(x₂) ∆х₂ - f(x₃)∆х₃ ) ∆х_i=lim f₁(x_i)∆х_i+ limf₂(x_i)∆х_i – limf₃(x_i) ∆х_i= f₁(х)dх +

+ f₂(х)dх – f₃(х)dх.

7⁰. Если отрезок интегрирования разбит на части (a < c < b), то интеграл на всем отрезке равен сумме интегралов на каждой из частей

a

c

b

x

= ,

Доказательство: Разобьём [а,в] на п частичных интервалов [а,х₁], [х₁,х₂], …, [х_п–1,в] длиной соответственно ∆х₁, ∆х₂, …, ∆х_п так, чтобы точка с была точкой деления. Пусть, например, х_т = с (т < п). Тогда интегральная сумма f(x_i) ∆х_i соответствующая интервалу [а,в], разобьётся на две суммы: f(x_i) ∆х_i=f(x_i) ∆х_i+f(x_i)∆х_i соответствующие интервалам [а,с] и [с,в].

Переходя к пределу при неопределённом уменьшении длины максимального частного интервала ∆х_i, то есть, при max ∆х_i 0, будем иметь f(х)dх=f(х)dх+ f(х)dх,

8⁰. (о среднем значении определённого интеграла). Если функция f(х) непрерывна на [а,в], то внутри него найдётся такая точка с, что f(х)dх = (в–а) f(с) .

Доказательство: Так как функция f(х) непрерывна на [а,в], то она достигает своего наибольшего и наименьшего значений М и т на [а,в]. Произведём обычное разбиение интервала [а,в], на п частичных интервалов длиной ∆х_i = х_i – х_i–1. (i = 1, …, п).

Так как f(х_i) > т при любом х_i, то f(х_i) ∆х_i > т∆х_i откуда f(х_i) ∆х_i > т ∆х_i или f(х_i) ∆х_i> т(в – а) так как ∆х =∆х₁+∆х₂+ … + ∆х_п =в – а. Так как, далее, f(х_i) < М, при любом х_i, то f(х_i) ∆х_i < М∆х_{i ,} а потому f(х_i) ∆х_i < М ∆х_i,, то есть, f(х_i)∆х_i< <М(в – а). Таким образом, имеем т(в – а) < f(х_i) ∆х_i < М(в – а). Переходя к пределу при max ∆х_i 0, получим неравенства т(в – а)< f(х)dх =М(в – а), m < f(х)dх/(в – а)< M

Из этих неравенств и теореме о непрерывной функции на [а,в], принимающей в этом [а,в] все промежуточные значения между своими наибольшими и наименьшими значениями, следует, что отношение m < f(х)dх/ (в – а)< M можно принять за значение f(с) функции f(х) в некоторой промежуточной точке с интервала [а,в] (т < f(с)< М).

Таким образом, f(х)dх) / (в – а) = f(с) или f(х)dх = (в – а)f(с).

Существует еще ряд важных свойств определенного интеграла, которые подводят нас к формуле для вычисления определенного интеграла. Эта формула называется формулой Ньютона – Лейбница для f(x) непрерывной на а; b.

Теорема (Формула Н-Л): Если f(x) непрерывна на [a,b] и F(x) – любая из ее первообразных, то имеет место формула: 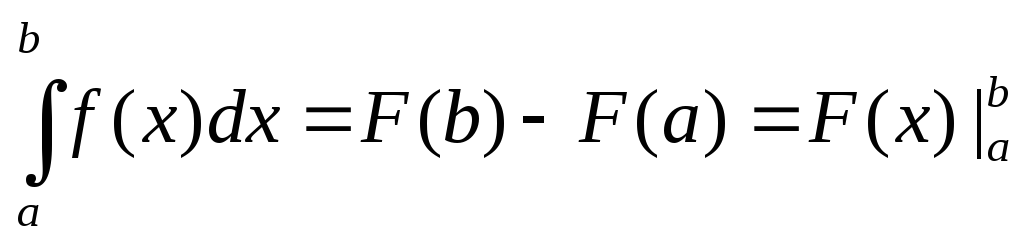- определенный интеграл равен разности значений первообразных на верхнем и нижнем пределах интегрирования.

Доказательство: Пусть F некоторая первообразная для функции f . Поскольку две первообразные отличаются друг от друга на некоторую постоянную, имеем

=F(х)+ С . Положим в последнем равенстве х = а. Так как =0, то F(а)+С=0, откуда С= – F(а). Подставляя найденное значение С, имеем =F(х)–F(а).

Полагая в последнем соотношении х=в и обозначая переменную t через х, окончательно получим равенство, указанное в теореме.

Формула Н-Л является одним из аппаратов для вычисления определенного интеграла, но для ее применения нужно соблюдать все требования.

1)

- вычислить.

Н

1

аходим первообразную для функции х², т.е. неопределенный интеграл от х², произвольную постоянную С приравняем к нулю.

0

= x³/3 │ = 1/3 – 0/3 = 1/3

Подставим в первообразную х³/3 вначале значение верхнего предела, равного 1, затем значение нижнего предела, равного 0 вместо х.

π/2

2

π/6

2

) Вычислить │= sin π/2 – sin π/6 = 1 – ½ = 1/2

3

-1

) Вычислить │ = 2² – 2⁴/4 – [ (-1)² – ((-1)⁴/4)] =

= 4 – 4 –(1- (1/4)) = -3/4.

  4.

Фактическое вычисление определённых интегралов осуществляется различными способами. В отдельных случаях определённый интеграл можно найти, непосредственно вычисляя предел соответствующей интегральной суммы. Однако большей частью такой переход к пределу затруднителен. Некоторые определённые интегралы удаётся вычислять с помощью предварительного отыскания неопределённых интегралов.

4.1. Пусть требуется в определённом интеграле

применить подстановку х = g(t). Тогда имеет место следующая формула замены переменных в определённом интеграле:

= f [g(t)]g’(t)dt,

где g() = а, g() = в.

Эту формулу мы докажем при условиях:

1. Функции g(t) и g’(t) непрерывны в [,].

1. Функция f(х) определена и непрерывна для всех значений, которые функция х = g(t) принимает в [,].

1. g() = а, g() = в.

Доказательство: Обозначим через М и т наибольшее и наименьшее значения функции х = g(t) в [,]. Пусть

F(х) = , т< х < М.

По теореме о подстановке в неопределённых интегралах для всех t из [,] справедливо равенство

F[g (t)] = f [g(t)]g’(t)dt.

Отсюда f [g(t)]g’(t)dt = F[g()] – F[g()] = F(в) – F(а)

Так как = F(в) – F(а)

то из сравнения последних двух равенств получим доказываемую формулу.

Вычислить интеграл

х ( 1+х²) dх =

Подставим 1+х² = t, то есть, х² = t² –1 . Имеем: t = 1, при х =0, t = 2, при х = 1. Так как dt = 2xdx , то xdx=dt/2

= tdt/2 = ½ t² /2 ₁|² =1 – ¼=3/4

4.2. Пусть функции u и v непрерывны вместе со своими производными в интервале [а,в]. Пусть, далее,

udv = uv _a|^b – vdu.

1. Вычислить интеграл.

х cos х dх

Положив f(х) = х, g (х) = sin х получим:

х cos х dх = х sin х| – sin х dх = –2

2. Вычислить интеграл

ln х dх.

Положив f(х) = ln х, (х) = х получим:

ln х dх = [х ln х] – х(dх/х) =

= [х ln х] – [х] = 2 ln2 – 1 = ln4 – 1

5. К вычислению определённых интегралов сводятся задачи об измерении площадей, ограниченных кривыми (задачи «нахождения квадратур»), длин дуг кривых («спрямление кривых»), площадей поверхностей тел, объёмов тел («нахождение кубатур»), а также задачи определения координат центров тяжести, моментов инерции, пути тела по известной скорости движения, работы, производимой силой, и многие другие задачи естествознания и техники.

5.1. Фигура, которую можно представить в виде объединения конечного числа попарно не налегающих допустимых прямоугольников, называется ступенчатой фигурой.

Пусть F любая ограниченная фигура, {P₁} множество ступенчатых фигур вписанных в F, {P₂} множество ступенчатых фигур описанных вокруг F. X_F множество площадей ступенчатых фигур вписанных в F, Y_F множество площадей ступенчатых фигур описанных около F.

Фигура F называется квадрируемой, если соответствующие ей числовые множества X_F и Y_F разделяются единственным числом S(F). Само это число называется площадью фигуры.

Теорема (критерий квадрируемости плоской фигуры): для того чтоб фигура F была квадрируема необходимо и достаточно чтобы ε>0 существовали такие ступенчатые фигуры P₁ и P₂ что выполняются 2 условия 1) 2) S(P₂)- S(P₁)<ε (Другими словами, для того чтобы плоская фигура F была квадрируемой, необходимо и достаточно, чтобы ее границу можно было заключить в ступенчатые фигуры, разность площадей которых меньше наперед заданного числа ε.)

Теорема: Если граница плоской фигуры состоит из конечного числа дуг Г_к являющихся графиками непрерывных функций, то данная фигура квадрируема.

Теорема: если функция y=f(x) непрерывна и неотрицательна на отрезке [a,b], то соответствующая криволинейная трапеция квадрируема и при этом ее площадь вычисляется по формуле

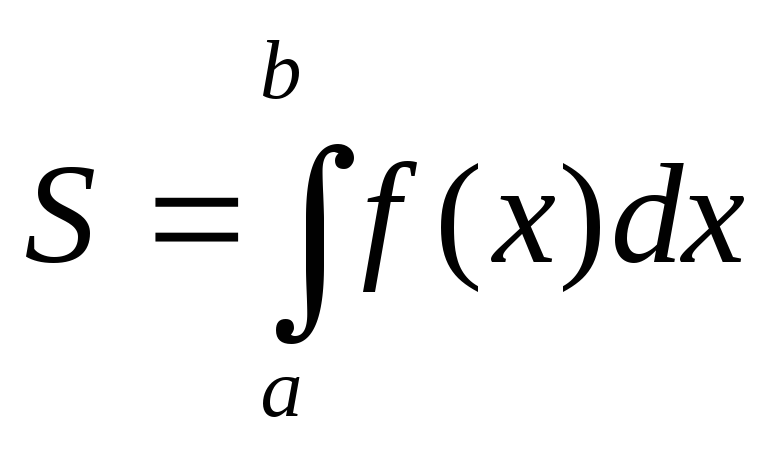
Доказательство: Возьмем ε>0, рассмотрим разбиение отрезка [a,b] точками x_k и составим суммы: площадь вписанной ступенчатой фигуры, площадь описанной ступенчатой фигуры. Т.к. f(x) непрерывна на [a,b], то она интегрируема на нем и тогда ε>0 δ>0, что разбиения, выполняется S(P₂)- S(P₁)<ε и при этом криволинейная трапеция: а это по критерию означает, что криволинейная трапеция квадрируемая, при этом множества и разделяются числом а множества S(P₁) и S(P₂) разделяются плоскостью криволинейной трапеции, но т.к эти множества совпадающие (согласно критерию) , то разделяющее их число единственно и поэтому