Вопросыи практика для тех 1 сем. 25.11.13

Экзаменационный билет

Часть А
А1. (1 балл)	Матрицы, определители; системы уравнений; векторы; прямые; пределы; производные.
А2. (1 балл)
А3. (1 балл)
А4. (1 балл)
А5. (1 балл)

Часть В

В1.1. Теоретический вопрос. (2 балла)

В1.2 Качественная задача к теор. вопросу. (1 балл)

В2.1. Теоретический вопрос. (2 балла)

В.2.2. Качественная задача к теор. вопросу.(1 балл)

Часть С

С1. Более сложное задание. (2 балла)

С2. Более сложное задание. (2 балла)

Если в части А менее 2 баллов, работа оценивается двойкой;

Вся работа оценивается следующим образом:

От 3 до 6 баллов – тройка

От 6 до 10 баллов – четверка

От 10 и выше - пятерка

Вопросы для подготовки к экзамену по математике

-Понятие матрицы. Записать матрицу в общем виде. Виды матриц.

- Понятие матрицы. Операции над матрицами.

-Определители. Определители 1-го,2-го, 3-го порядка. Правило треугольников.

-Вычисление определителя n-го порядка (основная теорема об определителях). Минор и алгебраическое дополнение.

- Ранг матрицы.

- Элементарные преобразования матриц.

- Система линейных уравнений. Основные понятия. Матрицы системы, решение системы. Классификация систем.

- Система n линейных уравнений c n неизвестными. Формулы Крамера (вывести).

- Метод Гаусса. Система m линейных уравнений c n неизвестными. (случай единственного решения и случай множества решений)

- Понятие вектора. Равные, коллинеарные, компланарные вектора, длина вектора. Сложение и вычитание векторов. Умножение вектора на число.

- Декартова система координат. Координаты вектора в декартовой прямоугольной системе координат. Разложение вектора по осям. Линейные операции над векторами в координатной форме

- Коллинеарные векторы. Необходимое и достаточное условие коллинеарности векторов. Соотношение между координатами и длинами коллинеарных векторов.

- Скалярное произведение векторов. Определение. Необходимое и достаточное условие перпендикулярности векторов. Скалярный квадрат вектора. Угол между векторами.

- Скалярное произведение векторов. Выражение скалярного произведения векторов и угла между векторами через координаты вектора.

- Общее уравнение прямой. Частные случаи общего уравнение прямой.

- Уравнение прямой с угловым коэффициентом. Частные случаи уравнения прямой с угловым коэффициентом.

- Уравнение прямой, проходящей через данную точку в данном направлении. Уравнение пучка прямых.

- Уравнение прямой, проходящей через две данные точки.

- Точка пересечения прямых.

- Угол между прямыми. Условия параллельности и перпендикулярности прямых.

- Расстояние от точки до прямой.

- Геометрический смысл линейных неравенств.

- Определение функции. Способы задания функции. Область определения функции. Основные свойства функции: четность, монотонность, периодичность, ограниченность.

- Определении предела функции в точке. Пояснить определение графически.

- Определении предела функции на бесконечности. Пояснить определение графически.

- Бесконечно малые функции и бесконечно большие функции. Свойства бесконечно малых функций и бесконечно большие функции.

- Бесконечно малые и бесконечно большие функции, теорема о связи бесконечно малых и бесконечно больших функций.

-Теорема о связи бесконечно малой функции с пределом

- Теоремы о пределах. Доказать любые две.

-Первый замечательный предел.

- Непрерывность функции в точке и на промежутке.

- Классификация точек разрыва.

- Определение производной. Физический смысл производной.

- Определение производной. Геометрический смысл производной.

- Связь непрерывности и дифференцируемости функции.

- Таблица производных и основные правила дифференцирования. Доказать любые два.

- Сложная функция. Производная сложной функции. Привести пример.

- Производные высших порядков. Привести пример.

Примерные задания для подготовки к части А

Векторы

-Определить, имеет ли четырехугольник ABCD прямые углы, если А(1;-2;2), B(1;4;0), C(-4;1;1) и D(-5;-5;3).

-. Векторы составляют угол 60, причем . Определить и , .

- Даны точки P(0; -3: 6), Q(2; -2: -1) и R(5; 1; -6). Вычислить ,

- Даны два вектора а (2;1;-2) и в(-1;1;1). Найти координаты вектора с=3а-2в и его длину.

- Определить угол между векторами a=-i+j и b=i-2j+2k. Найти длину вектора с=а+2в.

- Векторы взаимно перпендикулярны. Если , вычислить .

- Даны координаты точек А (-1;3;-7), B (2;-1;5) и С (0;1;-5). Определить а) скалярное произведение векторов , б) выяснить, будут ли векторы колинеарны.

- В пространстве даны векторы (1, –5, 2), (0, 0, 1).Найти их скалярное произведение и выяснить, образуют они острый, прямой или тупой угол.

- коллинеарны ли векторов а = {-3;1,5;-4,5} и b = {-6;3;-9}? если да, то установить, какой длиннее и во сколько раз, как они направлены (в одну или в разные стороны).

Прямые.

- Построить прямую, проходящую через начало координат и через точку (-5;3), написать ее уравнение, найти угловой коэффициент.

- Построить прямую, отсекающую на оси ОУ отрезок в=-2 и составляющую с осью ОХ угол 135° . Записать ее уравнение в общем виде.

- Написать уравнение прямой, проходящей через точки А(-2;4) и В(1;5). Найти ее угловой коэффициент. точки ее пересечения с осями координат.

- Построить области, координаты точек которых удовлетворяют неравенствам

5+x < y, x<0, y> -7.

- Написать уравнение прямой, параллельной прямой 5х – 2у + 5 = 0 и проходящей через точку А(1;-2),.

- Написать уравнение прямой, перпендикулярной прямой 5х – 3у +1 = 0 и проходящей через точку А(-1;2),

- Стороны треугольника АВС заданы уравнениями АВ: x + y-7 = 0, АС: x – 3у + 1 =0 и ВС: x - 2y -1 = 0. Найти координаты вершин треугольника.

Записать уравнение высоты, проведенной из вершины А, уравнение медианы, проведенной из этой вершины, найти длину высоты, длину медианы.

- Даны вершины треугольника A (0;-2), B (3;-1) и C (5;7). Составить уравнения его сторон. Составить уравнения его высоты АК. Найти ее длину. Составить уравнение медианы, найти ее длину.

Системы

Решить систему уравнений методом Гаусса и Крамера,

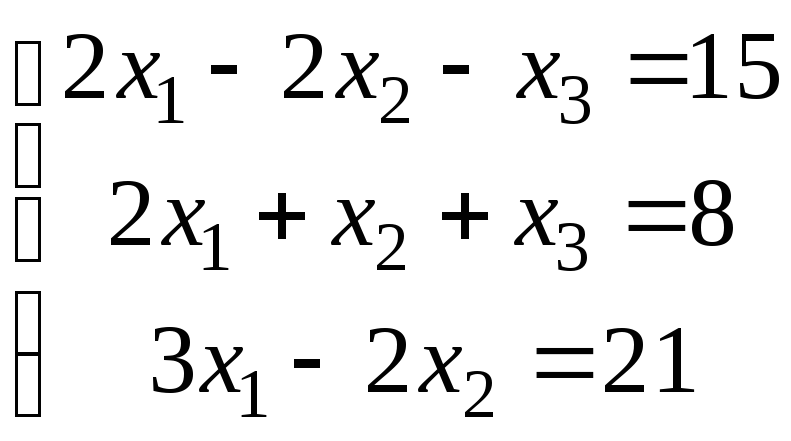
Решить систему уравнений а) методом Крамера и

б) методом Гаусса:

Матрицы и определители: Найти а) б)

Найти произведение матриц 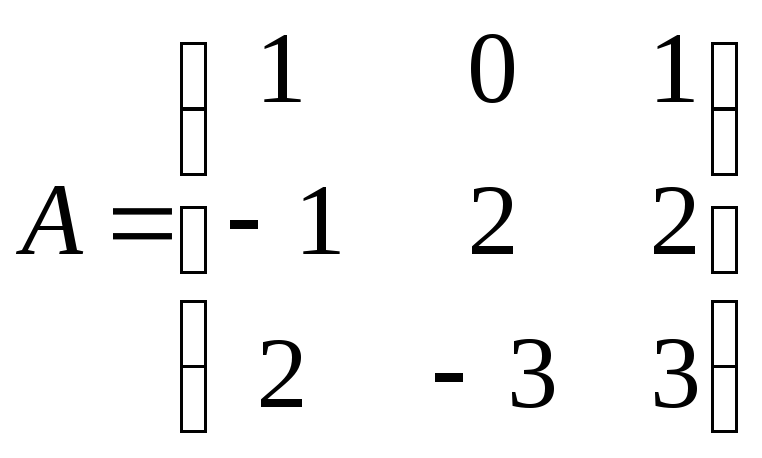и .

Найти СВ-ВС, если С= и В=.

Найти АВ^Т – 2В, если

Пределы

.

.

.

Производные

Найти производные

1. у=0,1х¹⁰+9х−10; 2. у=7⁷−x⁷ +arcsin0,7−e^x; 3. у=5х⁴ ctgx; 4. ;

5. ; 6. ; 7. у=7 cos(−x+4); 8. у=log₅(2−x⁹+); 9. у= ctg⁴x;

10. у=(3х-2)⁴ tgx