ФОПЭ / 1-9
.docx1.Этапы развития электроники. Роль полупроводниковой микроэлектроники и наноэлектроники в современном обществе.
Что такое электроника? – Это передача, приём, обработка и хранение информации спомощью электрических зарядов. Это наука, технические приёмы, промышленность. Что касается информации, то всегда, когда было человечество, это всё было. Человеческое мышление, разговорная речь, узелки на память, сигнальные костры, семафорный телеграф и т.д. – это приём, передача, обработка и хранение информации. И это было не меньше чем 5000 лет. Но только недавно, в конце 18 века, были изобретены телефон и телеграф – устройства для передачи и приёма информации с помощью электрических сигналов. Это – начало электроники, как она сейчас называется. Дальше электроника довольно быстро развивается. В 1895 г. Попов изобрёл и построил действующую модель радио – электронное устройство для беспроводной передачи информации - грозоотметчик. Герц провёл опыты по распространению радиоволн, Маркони развил и применил эти опыты для построения радио с выбором передающей радиостанции по длине волны излучения. Но в начале не было хорошего усилительного элемента для электрических устройств. Поэтому настоящее развитие электроники началось с 1904 г., когда была изобретенарадиолампа – диод, а в 1907 г. – триод. Они выглядят так, как показано на рис. Слева изображена радиолампа – диод, которая состоит из герметичного баллона, а внутри баллона– вакуум и несколько металлических конструкций с выведенными наружу электродами.

Радиолампы прошли очень большой путь развития. Появились более совершенные тетроды и пентоды – лампы с четырьмя и пятью электродами, обладающие большими коэффициентами усиления. Стали делать более сложные радиолампы: с более чем пятью электродами. Из них наибольшее распространение получили сдвоенные радиолампы: сдвоенные диоды, триоды, диод-триоды и т.д. Появились газонаполненные лампы – газотроны. В них есть газ, правда, находящийся под небольшим давлением. Обычно он ионизируется, появляются ионы – атомы без электрона, т.е. имеющие положительный заряд. К началу Второй мировой войны уже появились электронные арифмометры – обработчики цифровой информации. Но настоящее развитие этой области электроники началось с возникновения электронных вычислительных машин (ЭВМ). Оно началось в 1948 году – в США была сделана первая ЭВМ на радиолампах – ЭНИАК. Транзисторы очень быстро завоевали рынок сбыта. Уже в 1949 г. в США сделали первую транзисторную ЭВМ, аналогичную ЭНИАКу – т.е. через год после изобретения транзистора. Постепенно в ходе разработки технологии изготовления транзисторов пришли к диффузионной технологии, в основе которой лежит фотолитография. Кратко опишем фотолитографию. Её задачей является создание на поверхности кремния (он лучше всего подходит для фотолитографии) маски для диффузии, которая потом будет производиться локально. Эта маска должна выдерживать очень высокие температуры.Для этой цели годится оксид кремния, который получается очень просто путём окисления самого кремния при высоких температурах в парах воды и в кислороде. Его толщина порядки 1 мкм, но этого достаточно, чтобы не дать атомам примеси продиффундировать в полупроводник. Но в нужных местах в диоксиде кремния делают отверстия (окна), которые и будут определять, где пройдёт локальная диффузия.
2.Статистика носителей заряда в полупроводниках
Приводимость любых твердых тел определяется прежде всего концентрацией в них
электронов и дырок способных переносить заряд. Концентрация носителей заряда (этим
термином будем обозначать только свободные электроны и дырки) должна зависеть от
температуры, поскольку с увеличением температуры возрастает тепловая энергия решетки и
следовательно вероятность того, что какая то часть валентных связей будет нарушена и
соответственно возникнут электроны и дырки. Перечислим основные положения модели, которая используется для расчета концентрации носителей заряда в кристаллах:
• кристалл является квантовой системой, поэтому поведение всех находящихся в
нем электронов (и дырок) подчиняется закономерностям квантовой механики, т.е. как
локализованные (привязанные к атомам), так и “свободные” (способные перемещаться по
кристаллу) электроны находятся в определенных квантовых состояниях, характеризуемых
соответствующими энергетическими уровнями;
• в кристалле имеются состоящие из большого количества(1022эВ-1см-3) близко расположенных уровней зоны (расстояние между уровнями порядка 10-22эВ);
• на одном энергетическом уровне в соответствии с принципом запрета Паули не
может находиться более двух электронов с разным значением спина, т.е. электроны не могут
перемещаться по состояниям занятым другими электронами;
• в термодинамическом равновесии электроны распределяются по энергетическим
состояниям в соответствии с функцией распределения Ферми - Дирака:
![]()
где
![]() — среднее
число частиц в состоянии ,
— среднее
число частиц в состоянии ,
![]() — энергия
состояния ,
— энергия
состояния ,
![]() —
кратность
вырождения состояния (число состояний
с энергией ),
—
кратность
вырождения состояния (число состояний
с энергией ),
![]() —
химический
потенциал (который равен энергии Ферми
при абсолютном нуле температуры),
—
химический
потенциал (который равен энергии Ферми
при абсолютном нуле температуры),
![]() — постоянная
Больцмана,
— постоянная
Больцмана,

3. Энергетические зоны и свободные носители заряда в собственных и примесных полупроводниках
Уменьшение
высоты потенциальных барьеров при
сближении атомов приводит к тому, что
валентные электроны в металле перестают
быть локализованными в конкретном
атоме, а переходят от одного атома к
другому. Может показаться, что такие
переходы приводят к нарушению принципа
Паули и в любой момент в атоме может
оказаться несколько электронов с
одинаковой энергией. Однако при
образовании кристалла происходит не
только уменьшение высоты потенциального
барьера, но и качественное изменение
энергетических уровней электронов в
атомах. Воспользуемся соотношением
неопределенности энергии-времени ![]() ,
где
,
где ![]() - время
нахождения электрона в энергетическом
состоянии, характеризующемся интервалом
энергии от E до E+DE.
Величина DE определяет
ширину энергетического уровня, если
известно время пребывания на нем
электрона. В изолированном атоме
время Dt сколь
угодно велико, поэтому DE исчезающе
мало.В
кристалле скорость движения
электронов V ~ 105 м/с,
поэтому около данного узла решетки он
находится в течение приблизительно
10-15 с.
Приняв это значение времени за Dt,
получим ширину энергетического
уровня DE ~ 1
эВ. Такой результат свидетельствует о
том, что при образовании кристалла
энергетический уровень электрона
расщепляется в энергетическую
зону (рис.
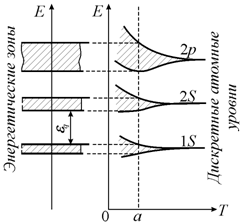
9.3). Эффект расщепления энергетических
уровней на зоны для металлического
натрия и элементов IV группы
таблицы Менделеева (алмаз, кремний и
германий) показан на рис. 9.4.
- время
нахождения электрона в энергетическом
состоянии, характеризующемся интервалом
энергии от E до E+DE.
Величина DE определяет
ширину энергетического уровня, если
известно время пребывания на нем
электрона. В изолированном атоме
время Dt сколь
угодно велико, поэтому DE исчезающе
мало.В
кристалле скорость движения
электронов V ~ 105 м/с,
поэтому около данного узла решетки он
находится в течение приблизительно
10-15 с.
Приняв это значение времени за Dt,
получим ширину энергетического
уровня DE ~ 1
эВ. Такой результат свидетельствует о
том, что при образовании кристалла
энергетический уровень электрона
расщепляется в энергетическую
зону (рис.
9.3). Эффект расщепления энергетических
уровней на зоны для металлического
натрия и элементов IV группы
таблицы Менделеева (алмаз, кремний и
германий) показан на рис. 9.4.
|
|
|
Рис. 9.3 Расщепление энергетических уровней на зоны |
|
|
|
Рис. 9.4. Образование энергетических зон: а - в металлическом натрии; б - в элементах IVгруппы элементов: алмаз, кремний и германий. |
Следовательно,
при образовании кристалла возникает
система энергетических зон. Однако
энергетическая зона – это не непрерывный
ряд значений энергии электронов, а
система близких друг к другу дискретных
уровней энергии.Если обобществленные
электроны достаточно сильно связаны
с атомом, то их потенциальную энергию
можно представить как ![]() ,
где
,
где ![]() −
потенциальная энергия электрона в
изолированном атоме, а dU –
поправочный член, учитывающий влияние
соседних атомов.По мере сближения
изолированных атомов и образования из
них решетки каждый атом попадает во
все возрастающее поле своих соседей.
Каждый из уровней атома расщепляется
на Nподуровней,
где N –
количество атомов в кристалле. При
ширине уровня 1 эВ и количестве атомов
в 1 см3,
равном 1023 атомов/см3,
расстояния между подуровнями чрезвычайно
малы, и такую область можно рассматривать
как энергетическую
зону с
квазинепрерывным спектром энергетических
состояний. Следовательно, моноэнергетический
уровень расщепляется в энергетическую
зону, получившую название зоны
разрешенных энергий.
Зоны разрешенных энергий отделены друг
от друга зонами
запрещенных энергий.
−
потенциальная энергия электрона в
изолированном атоме, а dU –
поправочный член, учитывающий влияние
соседних атомов.По мере сближения
изолированных атомов и образования из
них решетки каждый атом попадает во
все возрастающее поле своих соседей.
Каждый из уровней атома расщепляется
на Nподуровней,
где N –
количество атомов в кристалле. При
ширине уровня 1 эВ и количестве атомов
в 1 см3,
равном 1023 атомов/см3,
расстояния между подуровнями чрезвычайно
малы, и такую область можно рассматривать
как энергетическую
зону с
квазинепрерывным спектром энергетических
состояний. Следовательно, моноэнергетический
уровень расщепляется в энергетическую
зону, получившую название зоны
разрешенных энергий.
Зоны разрешенных энергий отделены друг
от друга зонами
запрещенных энергий.
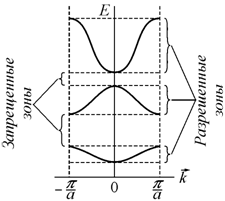
Выясним
физический смысл существования
запрещенных зон. Рассмотрим одномерную
решетку (линейную цепочку одинаковых
атомов) с периодом а.
В этом случае распределение электронов
по энергиям можно изобразить в виде
приведенной зонной диаграммы (рис.
9.5). Это распределение характеризуется
разрывом при значениях волнового
числа ![]() ,
что и создает область запрещенных
энергий. В одномерном случае формула
Вульфа-Брэггов
,
что и создает область запрещенных
энергий. В одномерном случае формула
Вульфа-Брэггов ![]() принимает
вид
принимает
вид
|
|
(9.25) |
Первые
отражения возникают при условии, что ![]() ,
и первая зона запрещенных энергий
(энергетическая щель) оказывается
соответствующей именно этим значениям
волнового числа. Последующие энергетические
щели возникают при следующих положительных
и отрицательных значениях k.
Отражение при
,
и первая зона запрещенных энергий
(энергетическая щель) оказывается
соответствующей именно этим значениям
волнового числа. Последующие энергетические
щели возникают при следующих положительных
и отрицательных значениях k.
Отражение при ![]() возникает
вследствие того, что волны, отраженные
от соседних атомов в цепочке, усиливаются
в результате интерференции, причем
разность фаз при данном значении
волнового числа k будет
составлять
возникает
вследствие того, что волны, отраженные
от соседних атомов в цепочке, усиливаются
в результате интерференции, причем
разность фаз при данном значении
волнового числа k будет
составлять ![]() .
Область пространства волновых векторов
(k-пространство)
между значениями
.
Область пространства волновых векторов
(k-пространство)
между значениями ![]() и
и ![]() ,
в этом примере носит название первой
зоны Бриллюэна. Внутри зоны Бриллюэна
энергия квазинепрерывна, а на границах
она имеет разрыв.Как было показано в
параграфе, 9.1 на амплитуду волновой
функции свободного электрона, в
периодическом поле ионных остовов
кристаллической решетки накладывается
дополнительное условие: она не остается
постоянной, а периодически изменяется
или, иначе говоря, модулирована с
периодом решетки. Волновая функция
электрона в этом случае имеет вид
блоховской функции (9.24). Исходя из
зонного характера энергии электрона,
можно утверждать, что внутри каждой
разрешенной энергетической зоны энергия
электрона E является
периодической функцией волнового
вектора
,
в этом примере носит название первой
зоны Бриллюэна. Внутри зоны Бриллюэна
энергия квазинепрерывна, а на границах
она имеет разрыв.Как было показано в
параграфе, 9.1 на амплитуду волновой
функции свободного электрона, в
периодическом поле ионных остовов
кристаллической решетки накладывается
дополнительное условие: она не остается
постоянной, а периодически изменяется
или, иначе говоря, модулирована с
периодом решетки. Волновая функция
электрона в этом случае имеет вид
блоховской функции (9.24). Исходя из
зонного характера энергии электрона,
можно утверждать, что внутри каждой
разрешенной энергетической зоны энергия
электрона E является
периодической функцией волнового
вектора ![]() (рис.
9.5).
(рис.
9.5).
|
|
|
Рис. 9.5 Зависимость энергии электрона от волнового вектора для одномерной моноатомной цепочки |
Конкретный
вид зависимости ![]() определяется
как симметрией кристалла, так и типом
атомов, его образующих. Анизотропия
кристалла обуславливает зависимость
определяется
как симметрией кристалла, так и типом
атомов, его образующих. Анизотропия
кристалла обуславливает зависимость ![]() от
кристаллографического направления.
На рис. 9.6 представлена трехмерная
картина изменения энергетических
уровней в периодическом поле двумерной
гексагональной кристаллической решетки
и дисперсия энергии электрона вдоль
направления наибольшей симметрии этой
решетки. Из рис. 9.6, б видно, что
энергетические уровни свободного
электрона претерпевают значительные
изменения при наложении периодического
потенциала. Более подробно анализ этих
зависимостей проведен в разделе 9.4.
от
кристаллографического направления.
На рис. 9.6 представлена трехмерная
картина изменения энергетических
уровней в периодическом поле двумерной
гексагональной кристаллической решетки
и дисперсия энергии электрона вдоль
направления наибольшей симметрии этой
решетки. Из рис. 9.6, б видно, что
энергетические уровни свободного
электрона претерпевают значительные
изменения при наложении периодического
потенциала. Более подробно анализ этих
зависимостей проведен в разделе 9.4.
|
|
||||||
|
Рис. 9.6. Зависимости энергии электрона от волнового вектора: а − изменение энергетических уровней свободного электрона, находящегося в поле ненулевого периодического потенциала в случае двумерной гексагональной решетки; б − дисперсия энергии вдоль направлений наибольшей симметрии гексагональной решетки (пунктир показывает уровни свободного электрона)
4. Влияние температуры на положение уровня Ферми в полупроводниках p- и n-типа Электроны, как частицы, обладающие полуцелым спином, подчиняются статистике Ферми–Дирака. Вероятность того, что электрон будет находиться в квантовом состоянии с энергией Е, выражается функцией Ферми–Дирака:
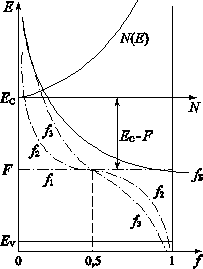
Здесь F – энергия Ферми, определяемая как значение энергии, при которой все состояния системы частиц, подчиняющихся статистике Ферми–Дирака заняты. Для электронного газа значение энергии Ферми совпадает со значением химического потенциала при T = 0 К и определяется как величина энергии, необходимая для изменения числа частиц в системе на единицу [79]. Также из формулы (10.12) видно, что энергию Ферми можно определить как энергию такого квантового состояния, вероятность заполнения которого равна 1/2. Вид функции Ферми–Дирака схематически показан на рис. 10.6.
При Т = 0 К она имеет вид разрывной функции. Для энергии меньшей энергии Ферми E < F функция Ферми-Дирака равна 1, а значит, все квантовые состояния при E < F заполнены электронами. Для энергии большей энергии Ферми E > F функция f = 0 и соответствующие квантовые состояния не заполнены. При Т > 0 функция Ферми-Дирака изображается непрерывной кривой и в узкой области энергий, порядка нескольких kBT, в окрестности точки E = F быстро изменяется от 1 до 0. Размытие функции Ферми-Дирака тем больше, чем выше температура.
5. Эффективная масса электрона. Зависимость эффективной массы электрона от энергии Известно,
что электрон в различных условиях
может обладать различной массой. Этот
феномен вызывает массу вопросов и,
самое главное, не понятна физическая
природа такого явления. Но оказывается,
что ларчик открывается очень просто.Если
в качестве плоскостей длинной линии
использовать сверхпроводник, то
магнитное поле на его поверхности,
равное удельному току, будет определяться
соотношением Если подставить значение глубины проникновения в соотношение (1) то получим неожиданный результат
Оказывается, что величина магнитного поля вовсе не зависит от величины заряда носителей тока, а зависит от их массы.Таким образом, удельная энергия магнитных полей
равна
кинетической энергия движения зарядов,
приходящаяся на единицу объёма. Но
магнитное поле, связанное с движением
носителей тока в поверхностном слое
сверхпроводника, существует не только
на его поверхности и в скин-слое. Объём
занимаемый магнитными полями
несоизмеримо больший, чем их объём в
самом сверхпроводнике. Если обозначить
длину линии, как
энергия же магнитных полей между плоскостями линии составит
(3)
Если
учесть, что глубина проникновения
магнитного поля в сверхпроводниках
составляет несколько сотен ангстрем,
то при макроскопических размерах
линии можно считать, что полная энергия
магнитных полей в ней определяется
соотношением (3).Поэтому, создание
магнитных полей
Очевидно,
что эффективная масса электрона по
сравнению с массой свободного электрона
возрастает при этом в
6. Зонная структура полупроводников Согласно постулатам Бора энергетические уровни для электронов в изолированном атоме имеют дискретные значения. Твердое тело представляет собой ансамбль отдельных атомов, химическая связь между которыми объединяет их в кристаллическую решетку. Если твердое тело состоит из N атомов, то энергетические уровни оказываются N-кратно вырожденными. Электрическое поле ядер, или остовов атомов, выступает как возмущение, снимающее это вырождение. Дискретные моноэнергетические уровни атомов, составляющие твердое тело, расщепляются в энергетические зоны. Решение квантовых уравнений в приближении сильной или слабой связи дает качественно одну и ту же картину для структуры энергетических зон твердых тел. В обоих случаях разрешенные и запрещенные состояния для электронов чередуются и число состояний для электронов в разрешенных зонах равно числу атомов, что позволяет говорить о квазинепрерывном распределении энергетических уровней внутри разрешенных зон.Наибольшее значение для электронных свойств твердых тел имеют верхняя и следующая за ней разрешенные зоны энергий. В том случае, если между ними нет энергетического зазора, то твердое тело с такой зонной структурой является металлом. Если величина энергетической щели между этими зонами (обычно называемой запрещенной зоной) больше 3 эВ, то твердое тело является диэлектриком. И, наконец, если ширина запрещенной зоны Eg лежит в диапазоне (0,1 ÷ 3,0) эВ, то твердое тело принадлежит к классу полупроводников. В зависимости от сорта атомов, составляющих твердое тело, и конфигурации орбит валентных электронов реализуется тот или иной тип кристаллической решетки, а следовательно, и структура энергетических зон. На рисунке 1.1 приведена структура энергетических уровней в изолированном атоме кремния, а также схематическая структура энергетических зон, возникающих при сближении этих атомов и образовании монокристаллического кремния с решеткой так называемого алмазоподобного типа.Верхняя, не полностью заполненная, энергетическая зона в полупроводниках получила название зоны проводимости. Следующая за ней энергетическая зона получила название валентной зоны. Энергетическая щель запрещенных состояний между этими зонами называется запрещенной зоной. На зонных диаграммах положение дна зоны проводимости обозначают значком Ec, положение вершины валентной зоны - Ev, а ширину запрещенной зоны - Eg.Поскольку в полупроводниках ширина запрещенной зоны меняется в широком диапазоне, то вследствие этого в значительной мере меняется их удельная проводимость. По этой причине полупроводники классифицируют как вещества, имеющие при комнатной температуре удельную электрическую проводимость σ от 10-8 до 106 Ом·см, которая зависит в сильной степени от вида и количества примесей, структуры вещества и внешних условий: температуры, освещения (радиации), электрических и магнитных полей и т.д.Для диэлектриков ширина запрещенной зоны Еg > 3 эВ, величина удельной проводимости σ < 10-8Ом·см, удельное сопротивление ρ = 1/σ > 108 Ом·см. Для металлов величина удельной проводимости σ > 106 Ом·см.
Рис. 1.1. Структура энергетических уровней в изолированном атоме кремния, а также схематическая структура энергетических зон, возникающих при сближении этих атомов и образовании монокристаллического кремния
7. Статистика электронов и дырок в полупроводниках
8. Влияние температуры на концентрацию носителей в собственном полупроводнике Температура – один из решающих факторов, влияющих на электропроводность. Рост температуры это сообщение дополнительной энергии атомам, составляющим кристалл, переход электронов на более высокие уровни и переброс их через запрещённую зону в зону проводимости. С ростом температуры число таких перебросов увеличивается, в связи с чем наблюдается рост числа свободных носителей заряда, что и объясняет рост проводимости полупроводника. Как отмечалось выше, увеличить число носителей заряда в полупроводнике можно путём легирования его различными примесями (донорами или акцепторами).При изменении типа и концентрации электрически активных примесей в полупроводнике происходит смещение уровня Ферми (уровень Ферми или энергия Ферми – уровень отделяющий полностью заполненные электронные уровни от полностью незаполненных), что, в свою очередь, приводит к изменению концентрации носителей заряда обоих знаков, т. е. электронов и дырок. При введении донорных примесей уровень Ферми смещается вверх относительно середины запрещённой зоны Эi (рис. 25). При этом равновесная концентрация электронов n0 становится выше собственной ni при данной температуре. Если же полупроводник легируется акцепторными примесями, то уровень Ферми приближается к валентной зоне и n0 > ni .Носители заряда, концентрация которых оказывается преобладающей, называют основными, а носители заряда противоположного знака, т. е.с меньшей концентрацией принято называть неосновными. Например, в полупроводнике n-типа основными носителями заряда являются электроны, а неосновными – дырки. Если в таком полупроводнике увеличивать концентрацию доноров, то будет возрастать число электронов, переходящих в единицу времени с примесных уровней в зону проводимости. Однако по мере увеличения скорости тепловой генерации электронов и их накопления в свободной зоне начнёт возрастать и скорость встречного процесса – рекомбинации носителей заряда, что будет приводить к уменьшению равновесной концентрации дырок. Выражение n0p0 = ni2 часто называют соотношением «действующих масс» для носителей заряда. По сути своей оно аналогично уравнению равновесия химической реакции, например, реакции диссоциации бинарного соединения при взаимодействии с газовой фазой. Изменение концентрации одного из реагентов вызывает нарушение химического равновесия и стимулирует массоперенос через межфазную границу, который продолжается до тех пор, пока произведение давлений реагирующих веществ не достигнет равновесного значения.На рис. 26 в полулогафмическом масштабе представлены типичные варианты температурных зависимостей концентрации носителей заряда в полупроводнике. Подобная картина наблюдается в полупроводниках как с донорным, так и с акцепторным легированием.
9. Собственные и примесные полупроводники. Полупроводники – материалы, удельное сопротивление которых при нормальной температуре находится между значениями удельного сопротивления проводников и диэлектриков. При этом проводимость возникает в них при условии порогового энергетического воздействия: тепла (пороговая температура), электростатического поля (пороговый потенциал), излучения (пороговая частота) и др. С точки зрения зонной электронной теории и теории почти свободных электронов при пороговом воздействии осуществляется переход электронов из валентной зоны в зону проводимости.Как и в металлах, электрический ток в полупроводниках связан с движением носителей заряда. Если в металлах наличие свободных электронов обусловлено самой природой металлической связи, то появление носителей заряда в полупроводниках определяется рядом факторов, важнейшими из которых являются химическая чистота материала и температура. В зависимости от степени чистоты полупроводники подразделяются насобственные и примесные.Собственный – это такой полупроводник, в котором можно пренебречь влиянием примесей при данной температуре. Согласно зонной теории твёрдого тела для полупроводников характерно наличие не очень широкой запрещённой зоны на энергетической диаграмме. В собственном полупроводнике при температуре абсолютного нуля валентная зона полностью заполнена электронами, а зона проводимости пуста. Из-за блокирующего действия запрещённой зоны собственный полупроводник при 0 оК не обладает электропроводностью, т. е. подобен диэлектрику.При температурах, отличных от абсолютного нуля, имеется конечная вероятность того, что некоторые из электронов за счёт тепловых флуктуаций (неравномерного распределения тепловой энергии между частицами) преодолеют потенциальный барьер и окажутся в зоне проводимости. В собственном полупроводнике каждый переход электрона в зону проводимости сопровождается образованием дырки в валентной зоне. Благодаря дыркам электроны валентной зоны также принимают участие в процессе электропроводности за счет эстафетных переходов под действием электрического поля на более высокие освободившиеся энергетические уровни. Совокупное поведение электронов валентной зоны можно представить как движение дырок, обладающих положительным зарядом и некоторой эффективной массой.Чем выше температура и меньше ширина запрещённой зоны, тем выше скорость тепловой генерации носителей заряда (электронов и дырок). Одновременно с генерацией в полупроводнике непрерывно идёт и обратный процесс: рекомбинация носителей заряда, т. е. возвращение электронов в валентную зону с исчезновением пары носителей заряда (электрон–дырка). В результате протекания двух конкурирующих процессов в полупроводнике при любой температуре устанавливается некоторая равновесная концентрация электронов n0 и дырок р0. Специфика собственного полупроводника состоит в том, что в нём равновесная концентрация электронов равна равновесной концентрации дырок.Механизм собственной электропроводимости рассмотрим на примере кремния (IV группа Периодической системы элементов), который кристаллизуется в структуре алмаза . В этой структуре каждый атом находится в тетраэдрическом окружении четырех ближайших соседей, с которыми взаимодействует силами ковалентных связей. Четыре валентных электрона любого атома идут на образование четырёх ковалентных связей. Все химические связи оказываются замкнутыми и полностью насыщенными. Состояниям связанных электронов соответствуют энергетические уровни в валентной зоне.Валентные электроны, осуществляющие химические связи, не могут оторваться от своих атомов без значительных затрат энергии. Энергетические затраты на разрыв связи и освобождение электрона количественно выражаются шириной запрещённой зоны. Атомы, потерявшие электроны, превращаются в положительно заряженные ионы, а незаполненная валентная связь содержит энергетическую вакансию для электронов, т. е. проявляет себя как дырка. Положительно заряженный ион может заимствовать электрон от любого соседнего атома, что приведёт к перемещению дырки по кристаллу. Образовавшиеся электроны и дырки проводимости беспорядочно блуждают по решётке до тех пор, пока не рекомбинируют при встрече.
Рис.Схематическое представление собственной электропроводности полупроводника. Под действием внешнего электрического поля движение носителей заряда приобретает направленный характер. При этом перемещение дырки к отрицательному полюсу источника можно представить как эстафетный переход валентных электронов от одного атома к другому в направлении против поля. Однако работа большинства полупроводниковых приборов нарушается при появлении собственной электропроводности.Примесный – это такой полупроводник, электрофизические свойства которого в основном определяются примесями. Как правило, примеси создают отщеплённые уровни в запрещённой зоне полупроводника. При малой концентрации примесей расстояние между примесными атомами велико, их электронные оболочки не взаимодействуют друг с другом. Вследствие этого примесные энергетические уровни являются дискретными, т. е. не расщепляются в зону, как это имеет место для уровней основных атомов кристаллической решётки.Если примесные атомы находятся в узлах кристаллической решётки, то их называют примесями замещения, если в междоузлиях – примесями внедрения.Роль примесей могут играть и всевозможные дефекты структуры. К числу таких дефектов относятся, в первую очередь, вакансии и междоузельные атомы.
|