Лабы / ОКМвТС лабы / лаб5_Построение гистограммы последовательности данных при пом среды Matlab

Построение гистограммы последовательности данных при помощи среды Matlab

Цель работы: получение навыков построения гистограмм и работы с ними в среде

Matlab.

Часто при проведении физического эксперимента или компьютерного моделирования приходится иметь дело с большим объемом данных. Поэтому актуальным является вопрос их наглядного представления. Численные данные можно оформить в виде графиков или диаграмм различных видов. Можно привести следующие примеры диаграмм и графиков: линейная диаграмма, столбиковая диаграмма, полосчатая диаграмма, кумулятивная кривая (данные накапливаются с течением времени), пиктограмма (данные представляются в виде стилизованных изображений), логарифмическая диаграмма, круговая диаграмма и т.д. Гистограмма (столбиковая диаграмма) – это последовательность столбцов, каждый из которых опирается на один раздельный интервал, а высота столбца – это частота или количество случаев. Принято распределять горизонтальную шкалу на один раздельный интервал вправо и влево от полученного диапазона. Середина столбца совмещается с серединой интервала, на практике ее обычно изображают в форме контура, опуская вертикальные линии. Наряду с понятием «гистограмма» используется понятие «полигон распределения». Полигон распределения – это та же гистограмма, но линии соединяют середины столбцов каждого разрядного интервала. Так как на разрядах справа и слева от разрядов распределения частот, частота имеет нулевое значение, поэтому полигон распределения продолжают до горизонтальной оси в середине интервала ниже меньшей оценки и выше высшей оценки. Гистограмма наиболее легка для восприятия и используется в тех случаях когда всего одно распределение. Если надо сравнить два или более распределений, используют полигон, чтобы избежать запутанной картины.

При построении гистограммы (т.е. графического изображения распределения некоторой величины) необходимо задавать определенное число бинов, определяя тем самым, сколько данных попадет в каждый бин и графически изображать это в виде столбиковой или ступенчатой диаграммы. Бин – это число разбиений переменной на интервалы, относительно которой и будет вычисляться и строиться распределение. Например, если студенты имеют рост от 150 см до 200 см, то можно разбить этот интервал ростов на 10 бинов, по 5 см в каждом, т.е это интервалы от 150см до 155см и т.д. Итак , гистограмма показывает сколько студентов попадает в каждый интервал ростов или бинов.

В Matlab существует функция hist, которая при обращении к ней в виде hist(y) вычисляет и рисует гистограмму с 10 бинами, равномерно распределенными между ymax

и ymin . Кроме того, функция hist(y) может иметь второй аргумент. Если этот аргумент –

целое число, то это число определяет число бинов. Если второй аргумент – вектор, то этот вектор определяет центры используемых бинов. В этом случае центры бинов должны быть равноотстоящими, а координаты этих центров должны быть расположены в возрастающем порядке. При нарушении любого из этих условий результат становится непредсказуемым.

Классическая гистограмма характеризует числа попаданий значений элементов вектора Y в М интервалов с представлением этих чисел в виде столбцовой диаграммы. Для получения данных для гистограммы функция hist (у) может быть записана следующим образом:

N=hist(Y) возвращает вектор чисел попаданий для 10 интервалов, выбираемых автоматически. Если Y – матрица, то выдается массив данных о числе попаданий для ее столбцов.

N=hist(Y,М) аналогична рассмотренной выше команде, но используется М интервалов (где М – скаляр).

N=hist(Y,Х). Данная команда возвращает числа попаданий элементов вектора Y в интервалы, центры которых заданы элементами вектора Х.

Пример. Построить гистограмму для 1000 случайных чисел и вывести вектор с данными о

1

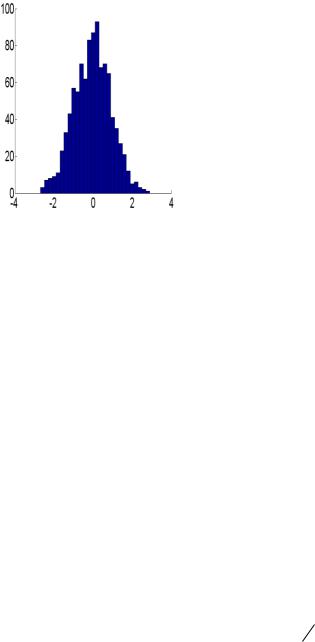
числах их попаданий в интервалы, заданные вектором х. Значения вектора х лежат в пределах от -3 до 3 с интервалом 0.2.

>>x=-3:0.2:3; % Задаются значения вектора х.

>>y=randn(1000,1); % Создается массив случайных чисел

>>hist(y,x) % Производится построение гистограммы

Врезультате запуска приведенной программы на экран будет выведен график, показанных на рис.1. Как видно из рис.1, распределение случайных чисел близко к нормальному закону. Еще большее соответствие этому закону можно наблюдать, если увеличить количество случайных чисел.

Опция Maker / Edges также предназначена для изменения вида отображения гистограммы. Выбрав Style, можно изменить вид символов, отображающих точки, по которым построена гистограмма. Размер этих символов задается при помощи Size. Цвет контура символов определяется Edge color, а цвет самих символов – Face color. При помощи Line style можно изменить тип линий, использующихся для отображения столбиков линий гистограммы, т.е. сделать линии пунктирными (Dashed line), в виде точек (Dotted line), точек и пунктиров (Dash-dot line) или вообще не использовать контурные линии для отображения столбиков (No line (none)). По умолчанию устанавливается опция Solid line (сплошная линия). Толщина контурных линий определяется при помощи

Line width, их цвет – при помощи Edge color.

Задание

1.Получите график, показанный на рис.1. Получив график, измените: 1) цвет гистограммы; 2) вид и размер символов, отображающих точки, по которым построена гистограмма; 3) тип и толщину контурных линий, использующихся для отображения столбиков линий гистограммы.

2.Получите аналогичный график, используя в 100 раз большее количество случайных чисел.

3.Постройте гистограмму распределения концентрации электронов ni в зависимости от про-

случайное число, имеющее различные значения для каждого i .

Литература

1.Коткин Г.Л., Черкасский В.С. Компьютерное моделирование физических процессов : Учеб. Пособие/Новосиб. ун- т. Новосибирск, 1999 - 128 с.

2.Дьяконов В.П. Matlab 6.5 SP1/7+Simulink 5/6. Основы применения. – М.: СОЛОН-Пресс, 2005. – 800 с.

3.Мэтьюз Дж.Г., Финк К.Д. Численные методы. Использование Matlab. – М.: Изд. дом «Вильямс», 2001. – 720 с.

2