
лекции МДТТ каз
.pdfТүйінсөздер: жай ж ктеу; К рделі ж ктеу; пластикалы шарт.
Негізгі сұрақтар (ұғымдар) жəне қысқаша мазмұны:
Бұл дəрістік сабақтарда ДҚДМ негізгі ұғымдары беріледі: жай жəне күрделі жүктеме; пластикалық шарттар; Треск-Сен-Венан аққыштық шарты; Мизес аққыштық шарты; идеал пластикалық ортаның көтеру қабілеттілігі; идеал пластикалық теорияның негізін беру.
Мазмұнын сипаттайтын негізгі схемалар, формулалар жəне б.қ., :
Жай жəне к рделі ж ктеу.
Күрделі кернеуленген күй жағдайында (32 – Сурет) кернеу тензорының компоненттері бір параметрге пропорционал өсетін болса, онда жүктеуді – жай ж ктеу дейді. Жай жүктеу кезінде кернеу тензорының түрі мен оның бас бағыттары өзгермейді.
К рделі ж ктеу кезінде кернеу тензорының бас осьтерінің бағыттары мен бас кернеулерінің өзара қатынастары өзгеруі мүмкін.
Мысал ретінде P + M – тəжірибесін қарастырамыз (32-Сурет) (Р – осьтік күш; М – бұраушы момент). Р,М координаталарында жүктеу процесі ОС сызығы ретінде бейнеленген (33-Сурет). Жай жүктеу кейбір сəулеге сəйкес келеді, мысалы ОО1 (33- Сурет). Басқа жүктеу жолы күрделі жүктеуге жатады, мысалы 33-суреттегі ОАВ – сызығы.
Күрделі кернеуленген күй жағдайында металдардың а ышты жəне беріктену процесін зерттеу үшін екі түрлі тəжірибе жасалады (32-Сурет: цилиндрлік жұқа құбыр):
P + M - тəжірибесі:
|
|
|
|
|
|
|
|
σ ϕ » 0,σ z = |
Ρ |
, |
||
|
|
|
|
|
|
|
|
|
||||
|
Μ |
|
|
|
|
|
|
2πah |
|
|||
τ ϕz = |
, мұндағы a - құбырдың орташа радиусы, |
h - құбырдың қалыңдығы. |
||||||||||
|
|
|||||||||||
2πa 2 h |
||||||||||||
|
P + p – |
тəжірибесі (Р – |
осьтік күш, р-ішкі қысым): |
|||||||||
|
|
|
sϕ » p |
a |
, sz = |
P |
|
, tϕz = 0, |
|
|
||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
h |
|
2pah |
|
|
||||
бұл жерде sr ~ p << sϕ , sr |
<< sz , себебі a / h >> 1, сондық-тан оны есептемеуге болады. |
|||||||||||
К рделі кернеуленген к й кезіндегі пластикалы деформацияны басталу шарттары
Енді күрделі кернеуленген күй кезінде металдардың серпімді күйден аққыштық күйге өтетінін сипаттайтын шарттарды қарастыруымыз қажет. Қазіргі кезде іс жүзінде
қолданып жүрген екі аққыштық шарттар бар. |
|
|||||||||||||||||
Треск-Сен-Венанны а ышты шарты: |
|
|||||||||||||||||
τ max |
= τ T , |
|
|
|
|
|
(11.1) |
|||||||||||
бұл жерде s1 ³ s2 ³ s3 |
|
|
|
|
|
– |
шарттары орындалады; енді бұл шарттар орындалмаған |
|||||||||||
жағдайда (11.1) шартын былай жазуға болады: |
|
|||||||||||||||||
2 |
|
τ |
1 |
|
= |
|
σ |
2 - σ 3 |
|
£ σ T , |
|
|||||||
|
|
|
|
|
||||||||||||||
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ |
|
|
|
= |
|
|
σ |
3 - σ 1 |
|
£ σ T , |
(11.2) |
|||||
|
|
|
|
|
|
|
||||||||||||
2 |
|
2 |
|
|
|
|||||||||||||
|
|
τ |
|
|
|
= |
|
σ |
1 - σ 2 |
|
£ σ T . |
|
||||||
|
|
|
|
|
|
|
||||||||||||
2 |
|
3 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
А ышты к й жағдайында (11.2) шарттарының біреуінде немесе екеуінде теңдік |
||||||||||||||||||
белгісі орын алу керек. |
Аққыштық шек sT > 0 |
болғандықтан, онда біруақытта үш бас |
||||||||||||||||
жанама кернеулердің sT |
тең болуы мүмкін емес. |
|
||||||||||||||||
Треск-Сен-Венан шарттарынан (11.1)-(11.2) мына қатынасты табамыз: |
||||||||||||||||||
σ T |
|
= 2τ T . |
|
|
|
|
|
(11.3) |
||||||||||

Бас координаталар осінде (11.2) шарттары дұрыс алты-жақты призманы – а ышты бетті анықтайды (34-Сурет). Призманың девиатор жазықтығындағы ізі дұрыс алтыбұрыш – а ышты исығы (35-Сурет).
Треск-Сен-Венан шарты (11.1) жалпы жағдайда металдардың аққыштық күйін дұрыс
сипаттайды, бірақ бұл шарт σ2 бас кернеуінің аққыштыққа |
ықпалын ескермейді. |
Тəжірибе деректері σ2 бас кернеуінің аққыштық күйге ықпалы бар екенін көрсетеді. |
|
Металдардың аққыштық күйін анықтайтын Мизес шарты: |
|
σi = σT , |
(11.4) |
мұндағы σi - кернеулер қарқындылығы, яғни Мизес алтыжақты призманы дөңгелек цилиндрмен алмастырған (36-Сурет). Бұл цилиндрдің девиатор жазықтығындағы ізі – шеңбер (35-Сурет), дұрыс алтыбұрышқа сырттай сызылған шеңбер.
Сығылмайтын идеал пластикалы денені к#теру абілеттілігі
32-Сурет |
33-Сурет |
34-Сурет |
Егер дененің материалы |
беріктенбейтін жəне сығыл-майтын болса, онда оны |
|
идеал пластикалы дейді. Идеал пластикалық материалдың диаграммасы 37-Суретте көрсетілген (мұндағы σi – кернеулер қарқындылығы, εi – деформациялар қарқындылығы) [1) ата идеал пластикалы дене; 2) серпімді идеал пластикалы дене].
35-Сурет 36-Сурет 37-Сурет Өзін тексеру үшін сұрақтар:
1. Мизес пластикалық критериясының Сен-Венан пластикалық критериясынан айырмашылығы неде? 2. Идеал пластикалық ортаның ерекше қасиеті қандай?
Ұсынатын əдебиет:
1.Работнов Ю.Н. Механика деформируемого твердого тела.- М.: Наука, 1988. - 712 с.
2.Искакбаев А. Деформацияланатын қатты дене механикасының негіздері. - Алматы: Изд- во Қазақ университетi, 2007. -176 бет.
№ 23 - 24 дəрісі.
Тақырыптың аты: Серпімдіпластикалы $быр шін Ламе есебі. Пластикалы процесті идеалданған диаграммалары.
Дəрістің мақсаты: олданбалы пластикалы теорияны негізгі модельдерін беру. Түйінсөздер: идеал ата пластикалы дене; серпімді идеал пластикалы дене;
сызы ты беріктенетін ата пластикалы дене; сызы ты беріктенетін серпімдіпластикалы дене.
Негізгі сұрақтар (ұғымдар) жəне қысқаша мазмұны:
Бұл дəрістік сабақтарда ДҚДМ негізгі ұғымдары беріледі: идеал қатаңпластикалық дене; серпімді идеал пластикалық дене; сызықты беріктенетін қатаңпластикалық дене; сызықты беріктенетін серпімдіпластикалық дене; серпімдіпластикалық құбыр үшін Ламе есебі;
пластикалық процестің идеалданған диаграммалары; қолданбалы пластикалық теорияның негізгі модельдерін беру.
Мазмұнын сипаттайтын негізгі схемалар, формулалар жəне б.қ., :
'алы $бырды серпімдіпластикалы к йін зертеу (жазы деформация)
Іштей жəне сырттай бірқалыпты қысылған қалың құбырды қарастырамыз; алдымен құбырдың материалы идеал пластикалық болсын дейміз (38-Сурет). Қысымдар мына шартты pa > pb қанағаттандырсын. Бұл есептің жағдайында sθ жəне sr – бас кернеулер болады:
sr - sθ |
+ r |
dsr |
= 0, |
(12.1) |
|
||||
|
|
dr |
|
|
яғни sr = sr (r), sθ = sθ (r). |
|
|
|
|
Егер ez = 0 жəне pa > pb |
ескерсек, онда sθ – |
созатын кернеу, сондықтан табамыз |
||
σ θ - σ r |
= 2k. |
(12.2) |
||
Осы екі теңдеуден (12.1), (12.2) жəне шекаралық шарттарды пайдалана отырып мына шешімді табамыз
pa - pb |
= 2k ln |
b |
, |
(12.3) |
|
||||
|
|
a |
|
|
яғни (12.3) – құбыр үшін пластикалық шарт. Осы шарт орындалған кезде құбыр идеал пластикалық күйде болады.
Сыртқы қысым |
pb = 0 кезінде, (12.3) формуласынан |
$бырды пластикалы |
||||
арсыласу шегін pT |
табамыз: |
|
|
|||
|
|
pT = 2k ln |
b |
, |
(12.4) |
|
|
|
|
||||
|
|
|
a |
|
|
|
мұндағы |
|
|
|
|
|
|
k = 0,5sT – |
Треск-Сен-Венан шарты бойынша, |
|
|
|||
k = 0,575sT |
– |
Мизес шарты бойынша. |
|
|
||
Іс жүзінде pT (12.4) |
мəнін сынды ысым ретінде қарауға бола-ды. Сондықтан, |
p < pT |
||||
кезінде құбырдың серпімді-пластикалық тепе-теңдігі орны ты болады, ал p ³ pT |
кезінде |
|||||
орны сыз. |
|
|
|
|
|
|
Енді мына жағдайды қарастырамыз, құбырдағы қысым пластикалық қарсыласу |
||||||
шегінен кіші, бірақ ол серпімді қарсыласу шегінен үлкен. Бұл жағдайда құбырдың көлденең қи-масында екі аумақ пайда болады: ішкі-пластикалық жəне сыртқы-серпімді (39-Сурет). Пластикалық ортаның серпімді ортаға қысымын q арқылы белгілейміз (39- Сурет). Енді пластикалық аумаққа байланысты, пластикалық шартты жазуға болады (39- Сурет: в) жағдай):
|
pa - q = sT ln bp , |
(12.5) |
мұндағы bp |
= c , бұл жерде Треск-Сен-Венан шартын пайда-ландық. |
|
|
a |
|
|
р |
|
|
|
|
|
|
|
|
B |
|
38 – Сурет |
39-Сурет |

Енді оңай болу үшін серпімділік шегін а ышты шекке тең деп алып (39-Сурет: б- жағдай), табамыз:
|
|
qc 2 − pb b2 |
|
(q − pb )c 2b |
2 |
|
|
||||||||||
σ θ = |
|
|
|
|
+ |
|
|
(b2 − c 2 )r 2 |
|
, |
|
||||||
|
b 2 − c 2 |
|
|
|
|||||||||||||
|
|
qc 2 − pb b 2 |
|
(q − pb )c 2b 2 |
|
||||||||||||
σ r = |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
, |
(12.6) |
|
|
b 2 − c 2 |
|
|
(b2 − c 2 )r 2 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||||
q − pb |
= σ T |
β e2 − 1 |
, |
|
|
|
|
|
|
|
|
||||||
2βe2 |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
мұндағы βe |
= |
b |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
Осы екі формулаларды (12.5) жəне (12.6) қосып, табамыз |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
pa − pb |
= σT ln βp − |
|
|
+ |
|
. |
|
|
(12.7) |
||||||||
2 |
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2βe |
|
|
|
|
||
Пластикалы процесті идеалданған диаграммалары
Күрделі кернеуленген күй кезіндегі дененің пластикалық процесін зерттейтін анықтауыш теңдеулерді бірөлшемді кернеу-деформация диаграммасы негізінде қорытып шығаруға болады. Ең көп қолданып жүрген төрт диаграмма 40-Суретте келтірілген. Бұл сұлбада М-массаның орын ауыстыруы пластикалық деформацияны сипаттайды ( $рғайкеліс), ал F – күші кернеудің ролін атқарады.
Бұл 40-Суретте көрсетілген модельдердің қасиеттері мынандай:
а) ата идеал пластикалы материал (серпімді аймағы жəне беріктену құбылысы
толық жоқ); |
|
|
|
|
|
|
б) – серпімді идеал пластикалы материал (серпімді аймағы бар, |
ал бірақ беріктену |
|||||
қасиеті жоқ); |
|
|
|
|
|
|
|
в) |
– |
сызы ты |
беріктенетін |
||
|
ата пластикалы материал (серпімді аймағы |
|||||
|
жоқ, ал беріктенуі сызықты); |
|
|
|||
|
г) |
– |
сызы ты |
беріктенетін |
||
|
серпімдіпластикалы |
материал |
(серпімді |
|||
|
аймағы бар, ал беріктенуі сызықты). |
|
||||
|
Бұл төрт механикалық модельдерде ең |
|||||
|
маңыздысы |
|
М-массасы |
мен |
жазық |
|
|
жазықтықтың арасындағы құрғақ үйкеліс, |
|||||
|
яғни $рға йкеліс – |
пластикалы элемент. |
||||
|
Егер Баушингер эффектісін еске алмасақ, онда |
|||||
|
сығу қисығы созу қисығының координат басы |
|||||
40-Сурет |
арқылы шағылысы болады (40-Сурет). |
|
||||
|
|
|
|
|
|
|
Өзін тексеру үшін сұрақтар:
1. Материалдың ақыштық шегі құбырдың ақыштық шегіне тең болама? 2. Құбырдың көтеру қабілеттілігін қалай анықтайды?
Ұсынатын əдебиет:
1.Работнов Ю.Н. Механика деформируемого твердого тела.- М.: Наука, 1988. - 712 с.
2.Искакбаев А. Деформацияланатын қатты дене механикасының негіздері. - Алматы: Изд- во Қазақ университетi, 2007. -176 бет.
№25 - 26 дəрісі.
Тақырыптың аты: Микрокернеулер жəне микроза ымданулар. За ымдану #лшемдері. Качанов-Работнов теориясы. 0за мерзім мəселелері. Новожилов жəне Ивлев модельдері.
Дəрістің мақсаты: Микрокенеулер жəне микроза ымдануларды материалдарды беріктігіне жəне ата дығына əсерін арастыру.
Түйінсөздер: микрокенеулер; микроза ымданулар; за ымдану лшемдері.
Негізгі сұрақтар (ұғымдар) жəне қысқаша мазмұны:
Бұл дəрістік сабақтарда ДҚДМ негізгі ұғымдары беріледі: микрокернеулер жəне микрозақымданулар; зақымдану өлшемдері; Качанов-Работнов теориясы; ұзақ мерзім мəселелері; Новожилов жəне Ивлев модельдері; микрокенеулер жəне микрозақымданулардың материалдардың беріктігіне жəне қатаңдығына əсерін қарастыру.
Мазмұнын сипаттайтын негізгі схемалар, формулалар жəне б.қ., :
Микрокернеулер жəне микроза ымдар
Барлық қатты денелерде жəне ерекше поликристалдарда микрокернеулер бар. Микрокернеулердің болуының ең бір себебі қатты денелердің құрылымдарының
микробіртексіздігі жəне микроанизотропиялығы. Микрокернеулер өрісіне өте үлкен ықпал жасайтын фактор – кез-келген деформация жəне оның ішінде ерекше-пластикалық деформация. Пластикалық деформация процесі айрықша бірқалыпты емес, сол себептен денеде кездейсоқ микродеформациялар өрісі пайда болады, ол өрістің сипаты
турбулентті болады.
Микрокернеулердің ең үлкен мəні болған жерлерде микросызаттар мен микрокеуектер пайда болады. Пластикалық деформацияның даму кезінде олардың мөлшері біртіндеп көбейеді, ал өлшемі өседі. Бұл процесс – за ымдарды жина -талуы, қираудың бірінші кезеңі болады. Денедегі микрозақымдардың бөлімдері бірігіп макросызат құраған кезде, бірінші кезең аяқталады. Қираудың екінші кезеңі кезінде макросызат таралып денені бөліктерге бөліп тастайды. Қирау процесінің бірінші кезеңін тұтас орта механика ұғымдары негізінде алғашқы рет зерттеген жəне оның моделін жасаған кеңес ғалымдары Л.М.Качанов жəне Ю.Н.Работнов болған. Қазіргі кезде тұтас орта механикасының бұл бағыты – за ымдану механикасы («damage mechanics») деп аталады. Қирау процесінің екінші кезеңін алғашқы рет зерттеп жəне моделін жасаған ағылшын ғалымы Гриффитс болған. Қазіргі кезде тұтас орта механикасының бұл бағыты
– ирау механикасы («fracture mechanics») деп аталады. 'ажып ирау кезінде қирау процесінің екі кезеңі орын алады. Мысал ретінде көміртекті болаттан жасалған үлгіні кернеу амплитудасы 333 МПа кезіндегі циклдік жүктемеге сынау тəжірибесінің нəтижесін қарастырамыз (41-Сурет). Бұл суретте абцисса осінде микросызаттардың ұзындығы (2а, мм), ал ордината осінде олардың өлшеміне байланысты жинақталған сомасы (пайда болған микросызаттардың жиынтық саны). Бұл тəжірибеде үлгінің салыстырмалы шыдаммерзімі N / N* = 0,97, мұндағы N – жүктеме циклінің саны, ал N* – үлгінің қирау циклінің саны. Бұл тəжірибенің негізгі нəтижесі мынандай: бастапқы кезеңде – бірінші кезеңде микросызаттардың санының өсуі өте тез болады ( h = 3 ), ал сонан кейін сызаттардың тығыздығының өсуі іс жүзінде аяқталады; осыдан кейін – екінші кезең басталады, яғни сызаттардың ұзындығы өсе бастайды ( h = 1,7 ) (41-Сурет).
Енді микрокернеулердің кері эффектілерге ықпалын қарастырамыз (42-Сурет). Бұл суретте көрсетілген модель– Д.Д.Ивлев моделі. АВ кесіндідегі серіппені – АВ элементі деп атаймыз; тұтқыр механизмін – В элементі; ВС кесіндідегі серіппені – ВС элементі; құрғақ үйкеліс механизмін – С элементі; СД кесін-дідегі серіппені – СД элементі деп атаймыз.
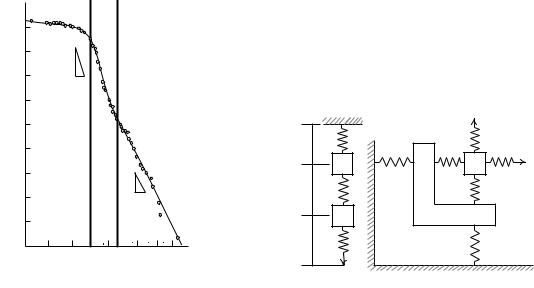
41-Сурет |
|
42-Сурет |
Алдымен В.В.Новожилов – |
Ю.И.Кадашевич моделін қарастырамыз: ВС,С жəне СД |
|
элементтерінен тұратын модель (42-Сурет). Модельдің деформация процесін зерттеу |
||
үшін, оны со-замыз: бұл жағдайда ВС элементінде лездік серпімді деформация пайда |
||
болады, сонан кейін С элементінен өтіп қайтымсыз қалдық деформация пайда болады. СД |
||
элементінде əсер ететін кернеуді – микрокернеу деп атаған, |
яғни СД элементі – Баушин- |
|
гер эффектісін сипаттайды – |
деформация процесіндегі |
пайда болған анизотропия |
эффектісі. Сонымен, беріксіздендіруді себебі микрокернеулер. |
||
Енді Ивлевтің моделін қарастырамыз (42-Сурет). Бұл жағдайда АВ элементінде |
||
лездік серпімді деформация пайда болады, сонан кейін тұтқыр механизмнің (В) əсерінен |
||
жылжымалылық деформация өседі (ВС кесіндіде) жəне, бұдан кейін С элементінің құрғақ |
||
үйкелісінен өткеннен кейін, қайтымсыз жылжымалылық қалдық деформация пайда |
||
болады (СД кесіндіде). Бұл модельде ВС элементінде əсер ететін кернеуді – микрокернеу |
||
деп атауға болады, оның əсерінен кері жылжымалылы құбылысы пайда болады, СД |
||
элементі – Баушингер эффектісін сипаттайды. Сондықтан, |
кері эффектілерді себебі – |
|
микро-кернеулер. |
|
|
Өзін тексеру үшін сұрақтар: |
|
|
1. Материалдың қандай сипаттамаларына микрозақымданулар əсер етеді? 2. |
||
Качанов-Работнов теориясында қандай зақымданулар қаралады? |
||
Ұсынатын əдебиет: |
|
|
1.Работнов Ю.Н. Механика деформируемого твердого тела.- М.: Наука, 1988. - 712 с.
2.Искакбаев А. Деформацияланатын қатты дене механикасының негіздері. - Алматы: Изд- во Қазақ университетi, 2007. -176 бет.
3.Гузь А.Н. Об описании и исследовании некоторых неклассических проблем механики разрушения и соответствующих механизмов // Успехи механики, Т. 1. Под редакцией А.Н.
Гузя. – Киев: «А.С.К.» 2005. – С.685 – 719.
№ 27 - 28 дəрісі.
Тақырыптың аты: Изотропты жəне кинематикалы беріктену. Пластикалы т$т ыр дене. Ағу теориясы.
Дəрістің мақсаты: Пластикалы ты ағу теориясыны негізін беру.
Түйінсөздер: изотропты беріктену; кинематикалы беріктену; пластикалы т т ыр дене.
Негізгі сұрақтар (ұғымдар) жəне қысқаша мазмұны:
Бұл дəрістік сабақтарда ДҚДМ негізгі ұғымдары беріледі: изотропты жəне кинематикалық беріктену; пластикалық тұтқыр дене; ағу теориясы; пластикалықтың ағу теориясының негізін беру.
Мазмұнын сипаттайтын негізгі схемалар, формулалар жəне б.қ., :
Изотропты жəне кинематикалы беріктену
Егер материал идеал пластикалы болса (40-Сурет: а, б), онда пластикалық деформация процесі кезінде а ышты бет өзгермейді жəне, сондықтан, пластикалық
шартты мына түрде жазуға болады: |
|
f1 (σij ) = 0, |
(14.1) |
мұндағы f1 (σij ) – а ышты функциясы деп аталады. Пласти-калық деформация процесі
кезінде материал беріктенетін болса, онда аққыштық бет өзгереді жəне ол бетті – ж ктеу беті деп атайды. Бұл бетті сипаттау үшін аққыштық функциясының (14.1) орнына ж ктеу функциясын кіргіземіз
|
f1* (σij , εijp , L)= 0, |
(14.2) |
мұндағы εijp – |
пластикалық деформациялар, ал L – беріктенуді сипаттайтын параметр. Бұл |
|
теңдеу (14.2) |
мынаны сипаттайды: f1* = 0 – |
серпімді аумақтың шекарасын анықтайды, |
f1* < 0 – жүктеу бетінің ішіндегі серпімді аумаққа сəйкес келеді, ал f1* > 0 – жүктеу бетінің
сыртқы аймағына сəйкес келеді жəне мағынасы жоқ.
Жүктеу функциясының (14.2) толық дифференциалын табамыз (14.3):
|
|
|
|
df1* |
= |
∂f1* |
dσij |
+ |
∂f1* |
dεijp + |
∂f1* |
dL. |
(14.3) |
||||
|
|
|
|
∂σij |
∂εijp |
∂L |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Егер f1* |
= 0 жəне |
|
|
∂f * |
dσij < 0, онда ж ксіздену процесі орын алады деп саналады; егер |
||||||||||||
|
|
|
1 |
||||||||||||||
|
|
∂σij |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
f1* = 0 жəне |
|
∂f * |
|
dσij |
= 0, |
|
|
|
|
|
егер f1* = 0 жəне |
||||||
|
1 |
|
онда |
бейтарап ж ктеу деп саналады; |
|||||||||||||
|
∂σij |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂f * |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
dσij |
> 0, |
онда |
активті |
ж ктеу |
процесі болып жатыр деп |
саналады. Жүктеу |
|||||||||
|
|
||||||||||||||||
|
∂σij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функциясының түрі (14.2) беріктену за ына байланысты анықталады. Біз бұл заңның екі қарапайым түрін қарастырамыз.
Изотропты беріктену болжамы: жүктеу кезінде аққыштық бет өзінің бастапқы түрін сақтай отырып, өзінің тек қана өлшемін өсіреді. Девиатор жазықтығында, Мизес жəне Треск-Сен-Венан критерийлеріне сəйкес келетін аққыштық қисықтарын бейнелеуге болады (43-Сурет): а) – Мизестің шеңберлері; б) Треск-Сен-Венанның дұрыс алтыбұрыштары.
Кинематикалы беріктену болжамы: жүктеу кезінде аққыштық бет өзінің бастапқы түрін жəне өлшемін сақтай отырып кернеулер кеңістігінде жаңа орынға ілгерілмелі орын ауыстырады. Бұл жағдайда аққыштық функциясын (14.1) былай жазу ке-рек:
f1 (σij − αij ) = 0, |
(14.4) |
мұндағы αij – жаңа аққыштық беттің центрінің координаталары. Егер беріктену сызықты болатын болса, онда
α ij = cε ijp , |
(14.5) |
бұл жерде с-тұрақты шама. Бірөлшемді жағдай кезіндегі Треск-Сен-Венан аққыштық қисығының орын ауыстыруы 44-Суретте көрсетілген.
Пластикалы т$т ыр ортаны моделі
Тұтқыр жəне пластикалық элементтерді қосқан кезде пластикалық тұтқыр ортаның модельдерін аламыз. Тұтқыр жəне пластикалық элементтерді параллель қосатын болсақ (45-Сурет; а) – пластикалы т$т ыр ортаны моделіне келеміз.
Бұл модельді алғашқы рет қарастырған ғалымдар Шведов (1900 ж.) жəне Бингамов (1922 ж.). Бұл модельдің анықтауыш қатынасы былай жазылады:
|
|
|
|
|
|
|
|
|
|
|
|
|
de |
|
|
|
|
|
|
|
|
|
|
s |
|
= sS |
+ m |
|
, |
(14.6) |
|||
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
dt |
||||||||
|
|
σ |
|
³ σ S ; ал егер |
|
σ |
|
< σ S |
|
|
|
|||||
егер |
|
|
|
|
– онда ортада деформация жоқ (46-Сурет). |
|
||||||||||
|
|
|
|
|
||||||||||||
Егер (14.6) sS = 0 болса, онда тұтқыр ортаның заңын ала-мыз, ал егер (5.22) μ = 0 –
онда идеал пластикалық ортаның заңы шығады.
Енді тұтқыр жəне пластикалық элементтерді тізбектеп қосатын болсақ (47-Сурет; б)
– онда жылжымалы-пластикалы ортаның моделін жасаймыз. Егер s < sS болса, онда бұл ортаның қасиеті тұтқыр сұйық тəріздес болады. Егер s = sS болса, онда бұл орта идеал пластикалық дене тəріздес ағады.
|
43-Сурет |
|
|
|
|
44 -Сурет |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
45 -Сурет  46-Сурет
46-Сурет
Пластикалы ағу теориясы
Қатаң идеал пластикалық материал үшін ағу за ы былай жазылады:
deij = sijdl, |
(14.7) |
мұндағы eij – деформация тензорының құраушылары, sij – |
кернеу девиаторының |
құраушылары, dλ – скалярлық функция, яғни жүктеу процесі кезінде өзгеруі мүмкін. Бұл қатынасты жазған кезде мынандай болжам жасалған: деформация өсімшелерінің жəне кернеулер тензорларының бас осьтері бірдей болады деп саналады.
Деформация өсімшесін серпімді жəне пластикалық бөлімдерге жіктейміз:
deij = deije + deijp , |
|
|
|
|
(14.8) |
||||||
мұндағы deije – серпімді деформация, |
|
deijp |
– пластикалық деформация. Осы қатынастарды |
||||||||
ескере отырып (14.7-14.8), Прандтль-Рейсс теңдеуін жазуға болады: |
|
||||||||||
|
deijp |
|
= sijdl, |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
(14.9) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
+ sijdl, |
|
|
||||
|
deij |
= deij |
|
|
|||||||
мұндағы |
|
|
|
|
|
|
|
|
|
|
|
e |
|
1 |
|
|
|
|
3n |
|
|
||
deij |
= |
|
|
dsij |
- |
|
|
|
|
dijds . |
(14.10) |
|
|
|
|
+ n |
|||||||
|
|
2G |
1 |
|
|
||||||
Серпімді идеал пластикалық материалды сипаттайтын ағу заңы (14.9), (14.10) формулаларымен анықталады.
Егер g = g(sij ) – кернеу құраушыларының функциясының төмендегідей қасиеті болатын болса (14.11):

dεijp = |
|
∂g |
dλ, |
(14.11) |
|||||
|
|
|
|||||||
|
|
|
∂σij |
|
|
|
|||
онда ол функцияны пластикалы потенциал деп атайды. |
|
||||||||
Кернеулер қарқындылығын мына түрде жазамыз: |
|
||||||||
|
|
|
|
|
|
|
|
|
|
σ |
|
= |
|
3 |
s s |
|
, |
(14.12) |
|
|
|
|
|
||||||
|
i |
|
|
2 ij |
ij |
|
|
||
мұндағы sij – кернеу девиаторының құраушылары.
Пластикалы деформация #сімшесіні ар ындылығын былай анықтаймыз:
dεip = |
2 |
dεijpdεijp . |
(14.13) |
|||
3 |
||||||
|
|
|
|
|||
Осы екі формулаларды (14.12), (14.13) пайдаланып, (14.9) теңдеуіндегі белгісіз dλ |
||||||
табамыз: |
|
|
3dεip |
|
||
dλ = |
|
(14.14) |
||||
|
. |
|||||
2σi |
||||||
Өзін тексеру үшін сұрақтар:
1. Металдардың изотропты беріктену механизмін түсіндіріңіз? 2. Металдардың кинематикалық беріктену механизмін түсіндіріңіз?
Ұсынатын əдебиет:
1.Работнов Ю.Н. Механика деформируемого твердого тела.- М.: Наука, 1988. - 712 с.
2.Искакбаев А. Деформацияланатын қатты дене механикасының негіздері. - Алматы: Изд- во Қазақ университетi, 2007. -176 бет.
№ 29 - 30 дəрісі.
Тақырыптың аты: Пластикалы деформациялы теориясы. '$быр шін Ламе
есебі. Генки параметрі. Ильюшин теориясы. |
|
|
|
|
Дəрістің мақсаты: |
Пластикалы |
деформациялы |
теориясыны |
негізгі |
болжамдарын беру. |
|
|
|
|
Түйінсөздер: кернеу |
ар ындылығы; |
деформация |
ар ындылығы; |
кернеу |
девиаторы; деформация девиаторы.
Негізгі сұрақтар (ұғымдар) жəне қысқаша мазмұны:
Бұл дəрістік сабақтарда ДҚДМ негізгі ұғымдары беріледі: кернеу қарқындылығы; деформация қарқындылығы; кернеу девиаторы; деформация девиаторы; пластикалық деформациялық теориясы; құбыр үшін Ламе есебі; Генки параметрі; Ильюшин теориясы; пластикалық деформациялық теориясының негізгі болжамдарын беру.
Мазмұнын сипаттайтын негізгі схемалар, формулалар жəне б.қ., :
Пластикалы ты деформациялы теориясы
Бұл теорияның негізгі анықтауыш қатынастарын мына түрде жазуға болады:
|
|
|
1 |
|
|
|
|
eij |
= ϕ + |
|
|
sij , |
(15.1) |
||
|
|
||||||
|
|
|
2G |
|
|||
ε ii |
= |
(1 − 2ν ) |
σ ii , |
(15.2) |
|||
|
|||||||
|
|
|
E |
|
|
|
|
мұндағы eij – деформация |
девиаторының құраушылары, ϕ – |
Генки параметрі деп |
|||||
аталады. Бұл параметрді былай анықтауға болады:
ϕ = |
3 |
|
ε p |
|
(15.3) |
|
|
i |
, |
||
2 |
σ i |
мұндағы ε ip -пластикалы деформацияны ар ындылығы:

|
ε p |
= |
|
|
2 |
ε pε p |
|
|
(15.4) |
|||
|
3 |
|
|
|||||||||
|
i |
|
|
|
|
ij ij |
|
|
|
|||
Енді (15.3), (15.4) қатынастарын ескере отырып, (15.1) қатынасынан табамыз |
||||||||||||
|
ε ijp |
= |
|
3 |
|
ε ip |
sij . |
|
|
(15.5) |
||
|
2 σ i |
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||
А.А.Ильюшиннің анықтауыш теңдеулерін келтіреміз: |
|
|||||||||||
|
σ = Kε , |
|
|
|
|
(15.6) |
||||||
|
σˆ 2 |
= |
2σ i |
εˆ 2 , |
|
|
(15.7) |
|||||
|
|
|
|
|||||||||
|
|
|
|
3ε i |
|
|
|
|
|
|||
|
σ i |
= f (ε i |
), |
|
|
(15.8) |
||||||
бұл жердегі K – көлемдік |
серпімділік |
модулі, σ – |
орташа кернеу, |
ε – көлемдік |
||||||||
деформация, σˆ 2 |
– кернеу девиаторы, εˆ 2 – |
деформация девиаторы, σi – |
кернеулер қар- |
|||||||||
қындылығы, ε i – |
деформациялар қарқындылығы. Белгісіз |
f (15.8) – функцияны бір осьтік |
||||||||||
таза созу тəжірибеден анықтайды (47 - Сурет).
Беріктенетін серпімдіпластикалы алы $бырды деформация процесін зерттеу
Есепті εz = 0 жəне pb = 0, pa = p |
жағдайында қарастырамыз. Таза бұралу |
тəжірибесінен, |
|
τ = f (γ ), |
(15.9) |
(15.9) тəуелділігі белгілі деп есептейміз. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
47-Сурет |
|
Біз қарастырып жатқан құбыр үшін, ең үлкен жанама кернеуді былай анықтауға |
|||||||||||||||||
болады |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
τ = σ θ |
|
− σ r |
. |
|
|
|
|
|
|
|
(15.10) |
||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Енді εz = 0 жəне материалдың сығылмайтынын ескеріп табамыз ( ν = 1/ 2 ): |
|
||||||||||||||||
γ = εθ |
|
− ε r |
= |
2B |
, |
|
|
|
|
(15.11) |
|||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
r 2 |
|
|
|
|
|
|
|
мұндағы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
1 |
|
(σ r |
|
−νσ θ ), |
|
|
|
|
|
||||||
ε r |
|
|
|
|
|
|
|
|
|
||||||||
E |
|
|
|
|
(15.12) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
1 |
|
(σ |
|
|
|
−νσ r ), |
|
|
|
|
||||||
|
= |
|
|
|
|
|
|
|
|
|
|||||||
εθ |
|
E |
θ |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
E |
|
|
|
|
|
B |
|
|
|
|||
σ r |
= |
|
|
|
|
|
|
|
A(1 |
+ν ) − |
|
|
|
(1 −ν ) , |
|
||
1 −ν |
2 |
|
r |
2 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
(15.13) |
|||||||
|
|
|
|
|
E |
|
|
|
|
|
B |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
σ θ |
= |
|
|
|
|
|
|
|
A(1 |
+ν ) + |
|
|
|
(1 −ν ) . |
|
||
|
1 −ν |
2 |
|
|
r |
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Өзін тексеру үшін сұрақтар:
1. Деформациялық теорияның ағу теориясынан айырмашылығы қандай? 2. Беріктену эффектісі материалдардың қандай сипатталарына ықпал етеді?
Ұсынатын əдебиет:
