
1.12. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ
.pdf
2.10.2014 |
1.12. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ. ТОЧКИ РАЗРЫВА - Математический анализ (часть 1) |
1.12. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ. ТОЧКИ РАЗРЫВА
Пусть функция f(x) определена в точке x0 и некоторой ее окрестности. Если существует
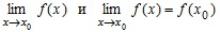 , то функция f(x) называется непрерывной в точке x0,
, то функция f(x) называется непрерывной в точке x0,
а x0 называется точкой непрерывности функции f(x).
На языке логики равенство 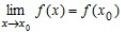 описывается формулой:
описывается формулой:
Используя понятия односторонних пределов, можно перефразировать определение так: функция называется непрерывной в точке x0, если она определена в точке x0 и некоторой ее
окрестности, если существуют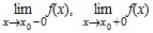 и
и 
Иногда приходится рассматривать непрерывность функции в точке x0справа или слева. Пусть функция определена в точке x0 и некоторой ее левой полуокрестности.
Если  , то говорят, что f(x) непрерывна в точке x0 слева.
, то говорят, что f(x) непрерывна в точке x0 слева.
Аналогично определяется непрерывность справа.
Пример 1. Функция f(x) = x3 определена на R.
Покажем, что f(x) непрерывна в точке x0 = 2.
Действительно,  , значит, f(x) = x3 непрерывна в точке x0 = 2.
, значит, f(x) = x3 непрерывна в точке x0 = 2.
Пример 2. 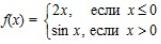 .
.
Покажем, что f(x) непрерывна в точке x0 = 0:
.
Так как  , то непрерывность функции f(x) в точкеx0 = 0 доказана.
, то непрерывность функции f(x) в точкеx0 = 0 доказана.
Дадим определение точек разрыва.
Пусть f(x) определена в окрестности точки x0, но может быть не определена в x0.
Точка x0 называется точкой разрыва для функции f(x), если в точке x0функция f(x) не определена, или 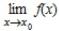 не существует, или
не существует, или  .
.
http://edu.imef.ru/personal/student_zievpo-00516_14/_layouts/efficientelrext/E-LearningContent/packId_112/lasgnId_81992/112_nepreryvnost_fu… 1/3

2.10.2014 |
1.12. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ. ТОЧКИ РАЗРЫВА - Математический анализ (часть 1) |
Пример 3. Функция 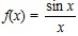 не определена в точке x0 = 0, но определена в любой окрестности этой точки, поэтому x0 = 0 является точкой разрыва для f(x).
не определена в точке x0 = 0, но определена в любой окрестности этой точки, поэтому x0 = 0 является точкой разрыва для f(x).
Пример 4. Функция 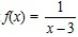 не определена в точке x0 = 3, x0 = 3 – точка разрыва для f(x).
не определена в точке x0 = 3, x0 = 3 – точка разрыва для f(x).
Пример 5. Пусть E(x) = «целая часть числа x», т.е. E(x) равно наибольшему целому числу, не
превосходящему x0. Так  и т.д. График y = E(x) представлен на рис. 1.14.
и т.д. График y = E(x) представлен на рис. 1.14.
Для x0 = 2: E(2) = 2,  .
.
Так как 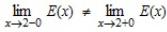 , то E(x) в точке x0 = 2 имеет разрыв, как и в любой другой целочисленной точке. Различают точки разрыва первого рода и второго рода.
, то E(x) в точке x0 = 2 имеет разрыв, как и в любой другой целочисленной точке. Различают точки разрыва первого рода и второго рода.
Точка разрыва x0 для функции f(x) называется точкой разрыва первого рода, если существуют
(конечные) пределы:  . В противном случае x0 – точка разрыва второго рода. В примере 5 точка x0= 2 является точкой разрыва первого рода, так как существуют
. В противном случае x0 – точка разрыва второго рода. В примере 5 точка x0= 2 является точкой разрыва первого рода, так как существуют
пределы |
. В примере 4 x0 = 3 – точка разрыва второго рода, так как |
.
Точка x0 разрыва первого рода, для которой 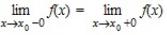 , называется точкой устранимого разрыва. Такой является точка x0 в примере 3. Если рассмотреть функцию
, называется точкой устранимого разрыва. Такой является точка x0 в примере 3. Если рассмотреть функцию
, то φ(x) непрерывна в точке x0 = 0, так как
. Доопределив функцию в точке x0 = 0, мы устранили
http://edu.imef.ru/personal/student_zievpo-00516_14/_layouts/efficientelrext/E-LearningContent/packId_112/lasgnId_81992/112_nepreryvnost_fu… 2/3

2.10.2014 |
1.12. НЕПРЕРЫВНОСТЬ ФУНКЦИИ В ТОЧКЕ. ТОЧКИ РАЗРЫВА - Математический анализ (часть 1) |
разрыв.
Рассмотрим операции над непрерывными функциями.
Теорема 1. Если функции f1(x) и f2(x) непрерывны в точке x0, то их сумма и произведение
также непрерывны в точке x0. Если, кроме того,f2(x0) ≠0, то частное  также непрерывно в точке x0.
также непрерывно в точке x0.
Теорема 2. Если функция u = φ(x) непрерывна в точке x0, а функция y = f(u) непрерывна в точке u0 = φ(x0), то сложная функция y = f(φ(x)) непрерывна в точке x0.
Установим непрерывность некоторых элементарных функций:
1.Всякая постоянная функция y = C непрерывна в каждой точке x0 R, так как
R, так как  .
.
2.Функция y = x непрерывна в любой точке x0, так как  . Тогда функция y = Cxn, где n
. Тогда функция y = Cxn, где n  N, непрерывна на всей числовой оси, как произведение непрерывных функций.
N, непрерывна на всей числовой оси, как произведение непрерывных функций.
3.Любой многочлен: y = a0 + a1x + a2x2 + ...+ anxn, непрерывен в каждой точке числовой оси, как сумма непрерывных функций.
4.Всякая рациональная дробь, являющаяся отношением двух многочленов , непрерывна во всех точках, в которых многочлен Q(x) не обращается в 0.
, непрерывна во всех точках, в которых многочлен Q(x) не обращается в 0.
5.Функция y = sinx, y = cosx непрерывны в точке x0 = 0, так как
Теорема 3. Всякая элементарная функция непрерывна в каждой точке, в которой она определена.
Если функция f(x) непрерывна в каждой точке интервала (a, b), то говорят, что f(x) непрерывна на интервале (a, b).
Пример 6. Функция  непрерывна на интервалах (–∞, 3) и (3, +∞), так как при x0≠ 3:
непрерывна на интервалах (–∞, 3) и (3, +∞), так как при x0≠ 3:  .
.
http://edu.imef.ru/personal/student_zievpo-00516_14/_layouts/efficientelrext/E-LearningContent/packId_112/lasgnId_81992/112_nepreryvnost_fu… 3/3
