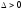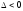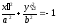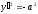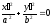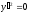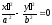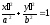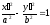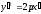7. Forms of representation of a line in the space.
There
are different ways of representation of a line in the space in some
Cartesian system of coordinates
 .
.
1.
An
equation of a line in parametric form.
Let a point with the radius-vector
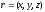 lies on a line in the space having non-zero directing vector
lies on a line in the space having non-zero directing vector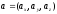 and passing through a point
and passing through a point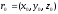 .
Then collinearity of vectors
.
Then collinearity of vectors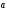 and
and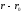 implies that an equation of line in the space must have the form:
implies that an equation of line in the space must have the form: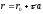 .
.
2.
An
equation of a line in canonic form.
If we exclude parameter
 from the scalar record of the equation
from the scalar record of the equation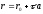 :
: then we obtain so-calledcanonic
equation
of line:
then we obtain so-calledcanonic
equation
of line:
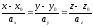 .
.
3.
An
equation of a line passing through two non-coinciding points
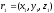 and
and
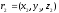 .
.
Since
directing vector of the line
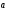 is collinear to vector
is collinear to vector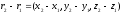 ,
an equation of line in vector form can be represented as
,
an equation of line in vector form can be represented as or
or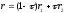 .
.
Excluding
parameter
 ,
we obtain an equation in the coordinate form:
,
we obtain an equation in the coordinate form:
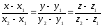 only
if
only
if
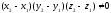 .
.
4.
An
equation of a line in the first vector form.
A line in the space can be given as a line of intersection of two
planes
 and
and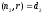 where
where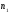 and
and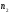 are non-collinear, normal vectors of these planes, and
are non-collinear, normal vectors of these planes, and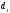 and
and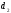 are some numbers.
are some numbers.
If
it is known a point
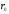 which is passed through by a given line then the radius-vector of any
point of this line satisfies to the following system of equations:
which is passed through by a given line then the radius-vector of any
point of this line satisfies to the following system of equations: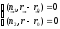 or in the coordinate form:
or in the coordinate form: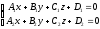 .
.
5.
An
equation of a line in the second vector form.
A line in the space can be given by means of the condition of
collinearity of vectors
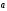 and
and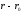 ,
i.e.
,
i.e.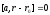 or
or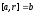 where
where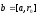 .
.
In
an orthonormal system of coordinates
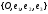 this equation of line in the space is:
this equation of line in the space is:
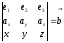 or
or
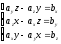 .
.
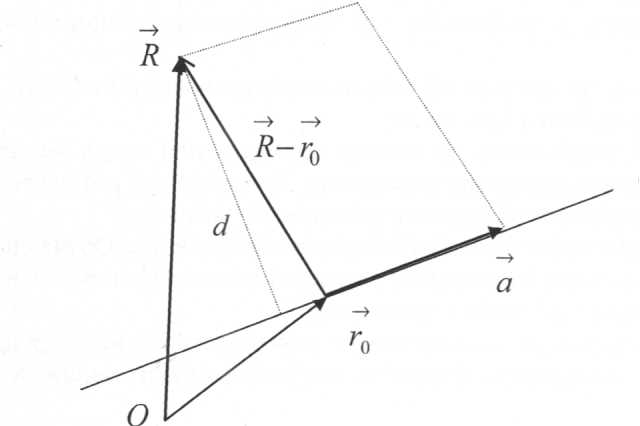
At
last, the distance
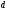 between some point with the radius-vector
between some point with the radius-vector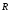 and a line
and a line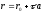 in the space can be found by using that
in the space can be found by using that is the area of parallelogram constructed on the pair of vectors is
equal to the module of their vector product.
is the area of parallelogram constructed on the pair of vectors is
equal to the module of their vector product.
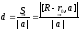 .
.
8. Curves of the second order in plane: theorem on canonic forms (case B = 0). Canonic system.
Let
an orthonormal system of coordinates
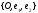 and some curve
and some curve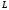 be given on a plane.
be given on a plane.
A
curve
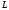 is called analgebraic
curve of the second order
if its equation in a given system of coordinates has the form:
is called analgebraic
curve of the second order
if its equation in a given system of coordinates has the form:
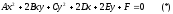
where
numbers
 and
and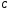 are not equal to zero simultaneously (
are not equal to zero simultaneously (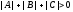 ),
and
),
and and
and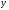 are the coordinates of the radius-vector of a point lying in the
curve
are the coordinates of the radius-vector of a point lying in the
curve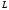 .
.
Introduce
the following notation:
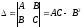 .
.
Theorem
1.
For every curve of the second order there exists an orthonormal
system of coordinates
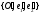 in which an equation of this curve has (for
in which an equation of this curve has (for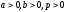 )
one of the following nine (calledcanonic)
forms:
)
one of the following nine (calledcanonic)
forms:
|
Type of curve |
|
|
|
|
Empty sets |
|
|
|
|
Points |
|
|
|
|
Coinciding lines |
|
|
|
|
Non-coinciding lines |
|
|
|
|
Curves |
Ellipse
|
Hyperbola
|
Parabola
|
Remark
1.
Curves of the second order for which
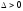 are related to anelliptic
type,
curves with
are related to anelliptic
type,
curves with
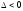 – to ahyperbolic
type,
and curves with
– to ahyperbolic
type,
and curves with
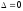 – to aparabolic
type.
– to aparabolic
type.
Remark 2. In order to find the canonic system of coordinates (i.e. the system of coordinates in which an equation has a canonic form) we write each of transition formulas, substitute them each other and obtain a final expression of the original coordinates through canonic ones:
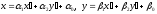
The
coefficients of these formulas give the coordinates of the origin of
canonic system of coordinates
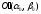 and its basis vectors
and its basis vectors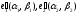 regarding to the original system.
regarding to the original system.