
- •1.Екі ортогональді проекциялық жазықтықтағы нүкте. Нүктелердің бір біріне қатысты
- •2.Проекциялаудың түрлері.
- •3. Түзуді проекциялаудың түрлері. Түзудің жазықтыққа қатысты орналасуы. Түзудің ізі.
- •4. Түзу мен нүктенің проекциялық жазықтықта бір біріне қатысты оналасуы.
- •5. Түзудің ұзындығын және жазықтыққа еңкею бұрышын анықтау.
- •9. Паралель орынауыстыру әдісі. Перпендикуляр проекциялық жазықтықтың өсі арқылы айналдыру.
- •10. Жазықтықтарды ауыстыру әдісі
- •11. Жазықтықтарды салу әдістері. Жазықтықтың проекциялық жазықтыққа катысты орналасуы.
- •12. Жазықтық. Жазықтықтың ізі. Жазықтықтағы басты сызықтар. Түзу мен жазықтықтың бір біріне қатысты орналасуы
- •13. Жазық бұрыштардың ортогональды проекциясының қасиеттері.
- •14. Монжа әдісі. Проекциялық жазықтықтар
- •15. Суреттерді компьютер жадында сақтау әдістері. Растрлық, векторлық және фракталдық
- •16. Қисық сызықтар. Қисық сызықтардың ортогоналды проекциясының қасиеттері.
- •17. Көпжақтылар және оның түрлері. Көпжақтыларды проекциялық жазықтықта көрсету.
- •18. Түзудің ұзындығын және еңкею бұрышын тікбұрышты үшбұрыш әдісімен салу
- •19. Сызу геометриясы және инженерлік графика пәнінің негізгі мақсаттары.
- •20. Аксонометриялық проекциялау әдісі.
- •21. Көпжақтылар мен жазықтықтардың қиылысуы.
- •22. Түзудің проекциялық жазықтықтардағы көрінісі. Түзудің ізін салу ережелері.
- •23. Ортақ жағдайдағы жазықтықтан жеке жағдайдағы жазықтыққа көшу әдістері.
- •24. Көпжақтының түзумен қиылысу нүктерлерін табу ережелері
- •25. Призма мен пирамиданың проекциясын көрсету әдістері.
- •26. Сызбаның негізгі және қосымша түрлері.
- •27. Кеңістіктік және жазық қисықтар. Оларды графикалық салу әдістері.
- •28. Аксонометриялық суреттерді салу әдістері
- •29. Техникалық сызбаларды салу
- •30. Жазықтықтардың ізін және оларды салу ережелері
18. Түзудің ұзындығын және еңкею бұрышын тікбұрышты үшбұрыш әдісімен салу
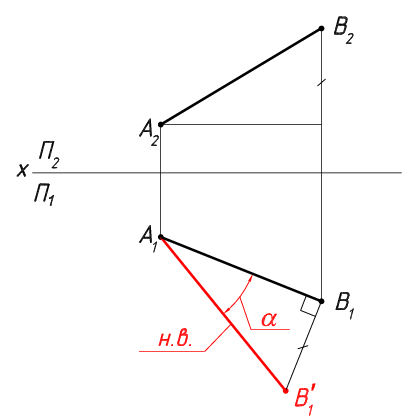
Ортақ жағдайдағы түзу проекциялық жазықтықтаға проекциялары натурал өлшемдерін бермейді. Бірінші катет – қиманың горизонталь проекциясы, екінші катет – z координатаның П2 проекция жазықтығындағы айырымы. Сәйкесінше тікбұрышты үшбұрыштың гипотенузасы – түзудің натурал өлшемі, ал α – түзудің горизонталь проекциялық жазықтыққа еңкею бұрышы болып табылады.
19. Сызу геометриясы және инженерлік графика пәнінің негізгі мақсаттары.
Сызықтық геометрия– кеңістіктегі фигуралар, олардың шешу әдістері және кеңістіктік есептерді жазықтықтағы суреттермен зерттейтін геометрияның бөлігі. Сызықты геометрияның әдістері техникалық сызудың теориялық базасы болып табылады. Бұл ғылымның мақсаты – машинасалу, архитектура және құрылыс объектілерінің пішінін салу, объектілер мен процестердің графикалық кескінін өңдеу.
Сызықтық геометрияды:
Кеңістіктегі фигураларды жазықтықта салудың әдістері;
Геометриялық есептердің графикалық және аналитикалық шешуінің әр түрлі әдістері;
Салынған объектінің геометриялық қасиеттерін зерттеу және түрлендіру әдістері;
Геометриялық объектілердің моделдеу зерттеледі
Сызу геометрияда салынған суреттер предметтердің ойдағы формасын елестетуге мүмкіндік беріп, кеңістіктік елестетуді дамытады. Сызу геометриядағы сызуларды салу әдісінің ережелері проекциялық әдіске негізделген. Проекциялық әдісте ең алдымен нүктенің проекциясын салу қарастырылады. Себебі кез келген кеңістіктік фигураларды салу осы фигура бойында жататын нүктелердің жиынтығы ретінде қарастырылады.
20. Аксонометриялық проекциялау әдісі.
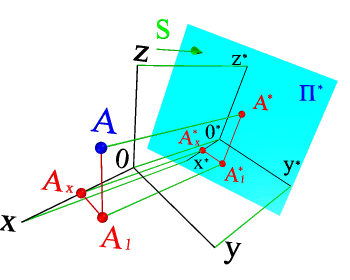
Аксонометрия сөзі – грек тілінен аударғанда ось бойынша өлшеу дегенді білдіреді. Аксонометриялық проекциялау кезінде беріліп отырған фигураны координаттар жүйесіне бекітеді және жазықыққа координаталар осімен қоса параллель сәулелер арқылы проекциялайды. А нүктесі xyz тікбұрышты координаттар жүйесіне қатысты болады, ал S векторы П* проекциялық жазықтыққа проекциялау бағытын көрсетеді. А1* аксонометриялық проекциясы А горизонталь прекцияның екінші ретті прекциясы ретінде саналады. П*-ға прекциялану кезіндегі координата осьтерінің қималарының бұрмалануы - бұрмалану коэффиценттерімен сипатталады. Бұрмалану коэффиценті деп – суреттегі ось қимасы проекциясының ұзындығының нағыз өлшемге қатынасын айтамыз. Х* осі бойынша бұрмалану коэффиценті u=0*x*/0x, ал y* және z* осьтері бойынша сәйкесінше υ=0*y*/0y и ω=0*z*/0z.
Бұрмалану коэффиценттеріне байланысты аксонометриялық проекцияладың түрлері :
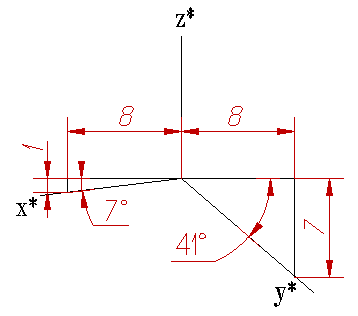
- Изометриялық – бұрмалану коэффиценттері барлық 3 ось бойынша өзара тең болады, яғни u=υ=ω;
- Диметриялық - бұрмалану коэффиценттері екі ось бойынша бірдей, ал үшіншісі қалған екеуінен айырмашылық жасайды.
Изометрия:

Диметрия:
21. Көпжақтылар мен жазықтықтардың қиылысуы.
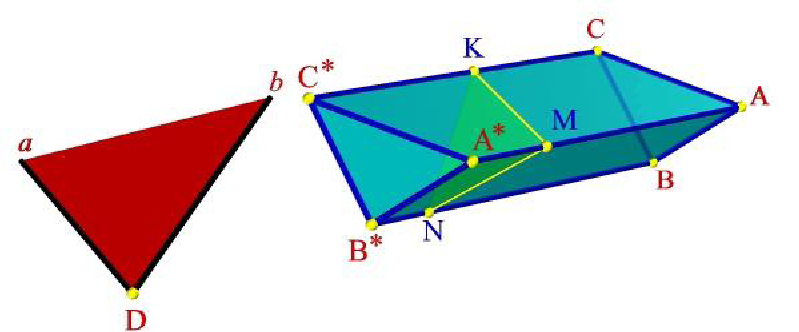
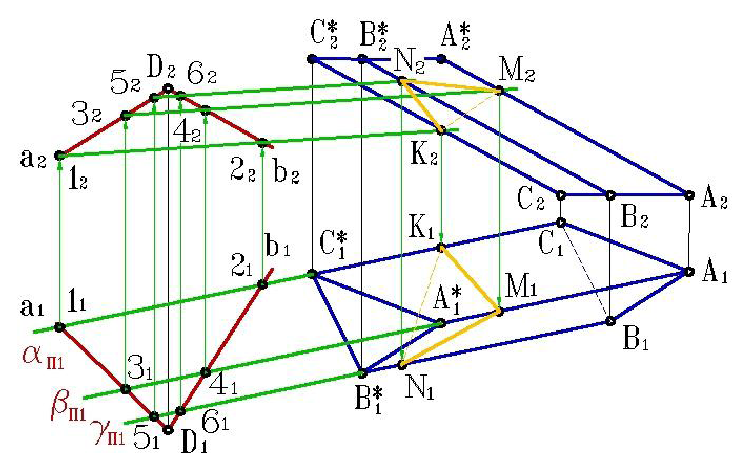
Пирамида мен призманың түзумен және жазықтықпен қиылысуы. Көпжақтының жзықтықпен қиылысуын көрсету үшін көпжақтының қабырғаларының жазықтықпен қиылысу нүктесін табу керек. Келесі суретте призманың EF және EG қиылысқан түзулерімен қиылысуы көрсетілген. Жазықтықты 𝛿 деп белгілейік. Қиылысу кезінде төбесі 𝛿 жазықтығы мен призма қабырғасының қиылысу нүктесі болатын төртбұрыш болып табылады. Бұл жағдайда тік призма және ол горизонталь проекциялық жазықтыққа паралель болғандықтан оның 𝜋1 жазықтықтағы қиылысуы тез табылады. A және D нүктесі арқылы өтетін призманың қабырғасы 𝛿 жазықтығымен қиылысатын К және L нүктесін табуға болады. Призманың қабырғалары арқылы өтетін 𝛼 және 𝛽 қосымша жазықтықтарды жүргізіп KL және MN кесінділері арқылы қиылысуды көрсетуге болады. Фронталдық проекцияда қиылысу кесінділері көрінетін және көрінбейтін жақтары болады.
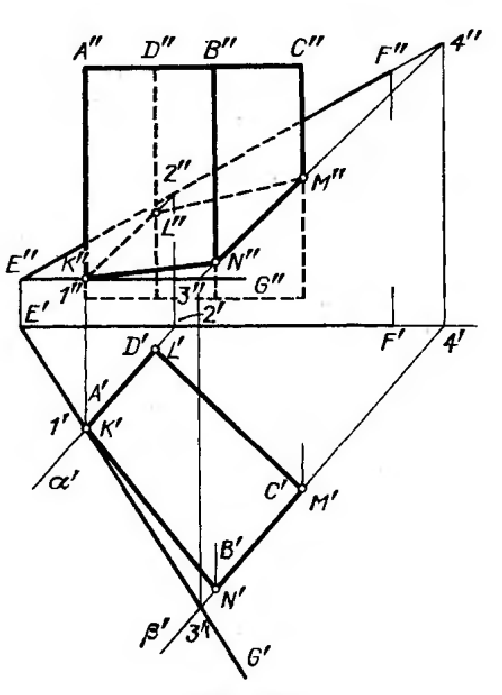
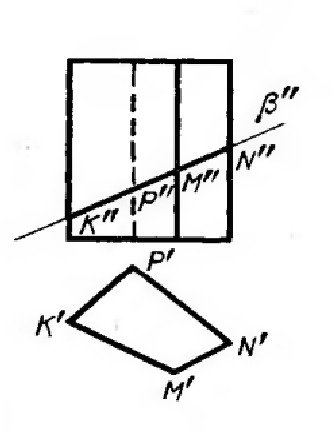
Егер де қиатын жазықтықтың біреуі проекциялық жазықтықтың біреуіне перпендикуляр болса (төмендегі суреттегідей), онда қиылысу проекциясы қосымша тұрғызусыз болады. 𝐾′′ 𝑃′′ 𝑀′′ 𝑁′′ фронталдық проекциясы 𝛽 жазықтығының ізінде орналасады, ал горизонталдық проекциясы 𝐾′ 𝑃′ 𝑀′ 𝑁′ призманың проекциясымен сәйкес келеді.
Көпжақтылардың жазықтықпен қиылысуының 2 әдісі бар:
Қиюшы жазықтықтың көпжақтардың әрбір жағымен қиылысуы – қиылысу сызықтары кобжақтардың әрбір жақтарынан тыс жатпайды.
Қиюшы жазықтықтың көпжақтылардың қабырғаларымен қиылысуы.
