
- •1. Молекулалық жүйенің статистикалық және термодинамикалық зерттеу әдістері,
- •4.Идеал газ молекулаларының орташа кинетикалық энергиясы.
- •6. Қысымның газдың тығыздығымен байланысын дәлелдеңіз және қысым мен тығыздықарқылы газдыњ молекулаларының орташа квадраттық жылдамдығын анықтаңыз.
- •7. Температура түсініктемесі. Температуралық шкала, реперлік нүктелер, температураны
- •8. Идеал газ күйінің теңдеуі, оның жалпы анықталмаған түрі. Қысымның газдың сандық
- •9. Менделеев-Клапейрон теңдеуін молекула-кинетикалық теорияның негізгі теңдеуінен
- •11. Молекулалық жүйедегі кездейсоқ оқиғалар мен кездейсоқ шамалар. Броундық
- •13. Изотермдік жағдайда ауаның қысымының Жердің бетінен биіктікке тәуелділігі. Барометрлік формула (қорытыңыз). Барометрлік формула
- •14.Үлестірілу функциясы туралы түсінік
- •15. Молекуланың жылдамдығына тәуелді функцияның (скалярлық, векторлық немесе
- •16. Максвеллдің үлестірілу функциясының жылдамдықтың х –компоненті үшін түрі,
- •17.Молекулалардың жылдамдықтар модулі бойынша үлестірілуі. Максвел заңы f(||)-ның V-қа тәуелділігін сипаттайтын графикті сызып, талдаңыз.
- •18. Әр түрлі температурада молекулалардың жылдамдықтар бойынша үлестірілу
- •20. Орташа арифметикалық жылдамдық, орташа квадраттық жылдамдығық және ең ықтимал жылдамдықтарды анықтайтын өрнектерді салыстырып байланыстарын талдаңыз
- •21. Максвеллдің формуласының өлшемсіз түрі. Салыстырмалы жылдамдық. F(u)
- •22. Ыдыстың қабырғасының бірлік ауданымен бірлік уақытта молекулалардың соқтығысу
- •23. Газдардың қасиеттерінің идеалдықтан ауытқуы. Идеал және нақты газдың
- •24. Эндрюстің эксперименттік изотермдері. Нақты газдар изотермдерін талдау.Критикалық немесе сындық изотерм, критикалық температура тк, критикалық қысым
- •26. Молекулааралық өзара әрекеттесуінің эмпирикалық потенциалы - қатты сфералар.
- •27. Молекулааралық өзара әрекеттесуінің эмпирикалық потенциалы - жұмсақ сфералар
- •28. Молекулааралық өзара әрекеттесуінің эмпирикалық потенциалы - Леннард-Джонс
- •31. Заттың критикалық күйі. Заттың p-V- күй диаграммасындағы критикалық күйін
- •38. Газдың көлемі өзгергендегі жұмыс. P f V тәуелділік бойынша жұмыстың
- •39.Идеал газдың жылусыйымдылығы. Меншікті жылусыйымдылық, мольдік
- •40. Изобарлық процестегі жылусыйымдылық.
- •41.Еркіндік дәрежелер саны. Газдардың жылусыйымдылығы арасындағы қатынастар
- •44. Термодинамиканың бірінші бастамасы мен идеал газ күйінің теңдеуін изотермдік
- •45. Термодинамиканың бірінші бастамасының дифференциалдық және толық
- •49. Жылудың механикалық жұмысқа айналуы. Циклдік процестер. Цикл жұмысы.
- •50. Карно циклі. Карно циклінің пайдалы әсер коэффициенті
- •Термодинамиканың дифференциалдық теңдеулерін қолданып, ішкі энергияның көлемге тәуелділігін анықтайық. Ішкі энергияның толық дифференциалы былай жазылады:
20. Орташа арифметикалық жылдамдық, орташа квадраттық жылдамдығық және ең ықтимал жылдамдықтарды анықтайтын өрнектерді салыстырып байланыстарын талдаңыз
 Осы
Осы
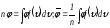 өрнектегі
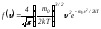
үлестірілу функциясының орнына (4.29)
анықтайтын шамасын қойып,
өрнектегі
үлестірілу функциясының орнына (4.29)
анықтайтын шамасын қойып,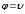 деп, оны 0 және
аралығын-дағы мүмкін болатын жылдамдықтар
бойынша интегралдап, орташа
арифметикалық жылдамдықтың
деп, оны 0 және
аралығын-дағы мүмкін болатын жылдамдықтар
бойынша интегралдап, орташа
арифметикалық жылдамдықтың
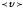 мәнін табамыз:
мәнін табамыз: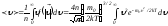 интегралдың
өрнегін қоссақ және есеп-теулер жүргізсек,
онда былай шығады:
интегралдың
өрнегін қоссақ және есеп-теулер жүргізсек,
онда былай шығады: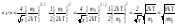 ,демек
,демек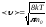 немесе
немесе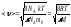 ,мұндағы
,мұндағы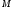 –
мольдік масса,
–
мольдік масса,
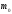 –молекула
массасы,
–молекула
массасы,
![]() –Авогадро
саны, Т–температура,
R–универсал
газ тұрақтысы.
–Авогадро
саны, Т–температура,
R–универсал
газ тұрақтысы.
(4.34)-ші
теңдеу молекуланың орташа
арифметикалық жылдам-дығын
анықтайды.4.5-суретіндегі қисықтың
үлестірілу функциясының максимал мәніне
сәйкес келетін жылдамдық модулін ең
ықтимал жылдамдық
деп айтады. Оны
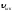 деп белгілейді.молекулалардың орташа
квадраттық жылдамдығы мынаған тең
болады:
деп белгілейді.молекулалардың орташа
квадраттық жылдамдығы мынаған тең
болады:![]() ,
,
демек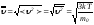
21. Максвеллдің формуласының өлшемсіз түрі. Салыстырмалы жылдамдық. F(u)
функцияның
u жылдамдыққа тәуелділігін сипаттайтын
графикті сызып, талдаңыз.
Көптеген мәселелерді шешу үшін Максвеллдің
үлестірілу функ-циясын анықтайтын
(4.28) формуланы салыстырмалы жылдамдықтар
арқылы жазу ыңғайлы. Онда молекулалар
жылдамдығы салыстыр-малы жылдамдық
арқылы бейнеленеді, мұндағы жылдамдықтың
бірлігі ретінде молекулалардың
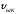 ең ықтимал жылдамдығын алады. Сондықтан
ең ықтимал жылдамдығын алады. Сондықтан салыстырмалы жылдамдық былай анықталады:
салыстырмалы жылдамдық былай анықталады: ,
(4.51)мұндағы
,
(4.51)мұндағы
 –
молекулалардың өзінің жылдамдығы, ал
–
молекулалардың өзінің жылдамдығы, ал
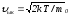 –
ықтимал жылдамдығы Т
температура
тұрақты болғанда.Максвеллдің
–
ықтимал жылдамдығы Т
температура
тұрақты болғанда.Максвеллдің
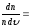
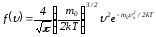 формуласына
екі қайтара
формуласына
екі қайтара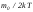 шама кіреді.Осы
шама кіреді.Осы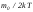 шаманы соған тең
шаманы соған тең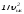 қатынасымен алмасты-рып және (4.51) ескеріп,
мына түрде жазуға болады:
қатынасымен алмасты-рып және (4.51) ескеріп,
мына түрде жазуға болады: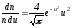 (4.52) Бұл
теңдеусалыстырмалы
жылдамдықтар
үшін Максвеллдің үлестірілуі, демек
Максвеллдің формуласының өлшемсіз
түрін
береді. (4.52)-ші қатынас –
универсалды, демек жан-жақты. Осы түрде
үлесті-рілу функциясы не газдың тегіне,
не температураға тәуелді емес. Молекулалар
жылдамдығының құраушылары үшін осыған
ұқсас тең-деуді жазуға болады. Егер
жылдамдықтың
(4.52) Бұл
теңдеусалыстырмалы
жылдамдықтар
үшін Максвеллдің үлестірілуі, демек
Максвеллдің формуласының өлшемсіз
түрін
береді. (4.52)-ші қатынас –
универсалды, демек жан-жақты. Осы түрде
үлесті-рілу функциясы не газдың тегіне,
не температураға тәуелді емес. Молекулалар
жылдамдығының құраушылары үшін осыған
ұқсас тең-деуді жазуға болады. Егер
жылдамдықтың
 -компонентін
алсақ, онда салыстырмалы жылдамдық
мынаған тең болады:
-компонентін
алсақ, онда салыстырмалы жылдамдық
мынаған тең болады: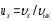 .
(4.53) Онда, (4.18) бойынша молекулалар
жылдамдығының құраушы-лары үшін
анықталатын үлестірілу функциясының
өлшемсіз түрі былай жазылады:
.
(4.53) Онда, (4.18) бойынша молекулалар
жылдамдығының құраушы-лары үшін
анықталатын үлестірілу функциясының
өлшемсіз түрі былай жазылады:
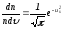 (4.54)
(4.54)
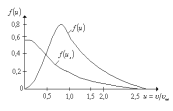
(4.10)-сурет
салыстырмалы жылдамдықтар үшін үлестірілу
функ-циясын бейнелейді.(4.52) және (4.54)
теңдеулердің мәндерін алдын ала әр
түрлі
 және
және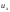 мәндері үшін есептеуге болады. 4.1-кестеде
осы функция-лардың мәндері келтірілген.
мәндері үшін есептеуге болады. 4.1-кестеде
осы функция-лардың мәндері келтірілген.
Мысалы,
жылдамдықтары 275 м/с
және 276 м/с
аралығында
болатын Т=300
К температурадағы
азот молекулаларының
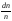 үлесін табу керек.
үлесін табу керек.
4.10-сурет

ық
Бұл
есепті шығару үшін (4.52)-ші теңдеуді
пайдалану қажет. Осыдан
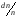 -ді
табамыз. Алдымен азот молекулаларының
300К-де ең ықтимал жылдамдығын есептейміз:
-ді
табамыз. Алдымен азот молекулаларының
300К-де ең ықтимал жылдамдығын есептейміз:
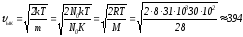 м/с.Онда
салыстырмалы жылдамдығы
м/с.Онда
салыстырмалы жылдамдығы
 мынаған тең болады
мынаған тең болады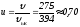 .
.
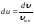 ,
бұл
,
бұл
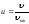 өрнегі бойынша анықталады. Есептің
шартында жылдамдықтар интервалы
өрнегі бойынша анықталады. Есептің
шартында жылдамдықтар интервалы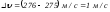 ,
өте аз шама, сондықтан
,
өте аз шама, сондықтан .4.1-кестеде
берілген үлестірілу функциясының
.4.1-кестеде
берілген үлестірілу функциясының салыс-тырмалы жылдамдыққа сәйкес мәні
салыс-тырмалы жылдамдыққа сәйкес мәні
 .
.
Осыдан
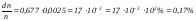 .
.
Сонымен
молекулалардың тек
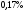 -нің
жылдамдықтары көрсе-тілген 275м/с
және 276 м/с
жылдамдықтар
интервалында жатады.
-нің
жылдамдықтары көрсе-тілген 275м/с
және 276 м/с
жылдамдықтар
интервалында жатады.
Қорытындылай
келе, мәселен, берілген жылдамдықтың
мәнінен қайсыбір жылдамдықтар артық
болатын барлық молекулалар үлесін
бағалап өтейік. Мұндай есептерді шығару
үшін (4.52)-ші формуланы қолдану ыңғайлы.
Жылдамдықтары
 -дан
артық болатын, демек онда белгілі
-дан
артық болатын, демек онда белгілі -дан
да артық болатын молекулалар үлесін
(4.52)-ші теңдеуді
-дан
да артық болатын молекулалар үлесін
(4.52)-ші теңдеуді
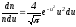 интегралдап
табамыз. Интегралдау шектері берілген
интегралдап
табамыз. Интегралдау шектері берілген
 жылдамдық пен шексіздік аралығында
жатады. Сонда молекулалар үлесін
жылдамдық пен шексіздік аралығында
жатады. Сонда молекулалар үлесін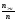 анықтайтын өрнегі мына түрде жазылады:
анықтайтын өрнегі мына түрде жазылады: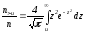 (4.55) мұндағы
(4.55) мұндағы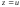 ,
,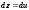 ,
, –
молекулалар саны, салыстырмалы
жылдамдықтары берілген
–
молекулалар саны, салыстырмалы
жылдамдықтары берілген
 жылдамдықтан үлкен. Сонымен есептеу
үшін (4.55)-гі интегралды табу қажет.Мысалы,
ең ықтимал жылдамдықтан артық жылдамдықпен
қозғалатын молекулалар үлесін анықтайық,
демек
жылдамдықтан үлкен. Сонымен есептеу
үшін (4.55)-гі интегралды табу қажет.Мысалы,
ең ықтимал жылдамдықтан артық жылдамдықпен
қозғалатын молекулалар үлесін анықтайық,
демек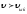 онда
онда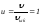 ,
осыған сәйкес келетін (4.55) интеграл мәні
0,5724 немесе
,
осыған сәйкес келетін (4.55) интеграл мәні
0,5724 немесе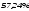 .
Жылдамдықтары
.
Жылдамдықтары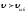 қозғалатын газ молекулалар саны
жартысынан көп.
қозғалатын газ молекулалар саны
жартысынан көп.
