
Вариант 2 Zhadi
.docx-
Отделение банка обслуживает 1200 клиентов, держащих свой вклад в этом банке. В данном интервале времени любой клиент независимо от остальных может провести операцию по вкладу с вероятностью 0,001. Какова вероятность того, что в данном интервале будет ровно 4 операции по вкладам?
Решение:
npq<4,8
1,996<4,8

λ =n*p=1,2

Ответ: 0,027
-
Для лица, дожившего до 26-летнего возраста, вероятность смерти на 30-м году жизни равна 0,005. Застрахована группа в 12000 человек 26-летнего возраста, причем каждый застрахованный внес 50 000 тенге страховых взносов за год. В случае смерти застрахованного страховая компания выплачивает наследникам 400 000 тенге. Какова вероятность того, что к концу года страховая компания:
-
окажется в убытке;
-
ее доход превысит 2 600 0000 тенге;
-
ее доход превысит 1 900 0000 тенге?
-
-
Негосударственный пенсионный фонд начисляет по пенсионным счетам
 годовых. 1 января 2009 года вкладчик
перечислил
годовых. 1 января 2009 года вкладчик
перечислил
 тенге. Какие проценты будут начислены
на эту сумму к 31 декабря 2014 года?
тенге. Какие проценты будут начислены
на эту сумму к 31 декабря 2014 года?
Решение:
S=P(1+i)n
S=57500(1+0.01)6=101864,75
I=S-P=101864,75-57500=44364,75 тг.
Ответ:I=44364тг.
-
Вкладчик внес на счет
 тенге. Банк гарантирует, что на протяжении
двух ближайших лет эффективная годовая
процентная ставка будет равна
тенге. Банк гарантирует, что на протяжении
двух ближайших лет эффективная годовая
процентная ставка будет равна
 .
Через два года банк установит процентную
ставку
.
Через два года банк установит процентную
ставку
 на следующие три года. Известно, что
новая ставка не выйдет за пределы
промежутка
на следующие три года. Известно, что
новая ставка не выйдет за пределы
промежутка
 .
Что можно сказать о сумме, которая будет
накоплена за четыре года?
.
Что можно сказать о сумме, которая будет
накоплена за четыре года?
S=P(1+i)n
S1=35000*(1+0,06)2=39326
S2=39326*(1+0,08)3=49539,43
S4=39326*(1+0,09)3=50928,31
-
Случайная величина
 – число выпадений тройки при четырех
подбрасываниях игральной кости. Для
этой случайной величины составить
закон распределения, найти и построить
функцию распределения, многоугольник
распределения, найти вероятность того,
что тройка выпадет менее двух раз.
– число выпадений тройки при четырех
подбрасываниях игральной кости. Для
этой случайной величины составить
закон распределения, найти и построить
функцию распределения, многоугольник
распределения, найти вероятность того,
что тройка выпадет менее двух раз. -
Для лица, дожившего до 30-летнего возраста, вероятность смерти на 35-м году жизни равна 0,007. Страховая компания предлагает застраховать жизнь на год со страховым взносом 25$. В случае смерти застрахованного страховая компания выплачивает наследникам 2000$. Какую прибыль ожидает получить компания с каждого застраховавшегося?
-
Клиенты банка, не связанные друг с другом, не возвращают кредиты в срок с вероятностью 0,1. Составить закон распределения случайной величины
 – числа возвращенных в срок кредитов
из 3 выданных. Найти вероятность
– числа возвращенных в срок кредитов
из 3 выданных. Найти вероятность
 .
.
Решение:
В
данном случае мы имеем дело с биномиальным
законом с
 и
и
 .
Случайная величина
.
Случайная величина
 – число возвращенных в срок кредитов
из трех выданных принимает значения:
– число возвращенных в срок кредитов
из трех выданных принимает значения:
 ,
,
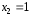 ,
,
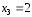 и
и
 .Соответствующие
им вероятности
.Соответствующие
им вероятности
 ,
,
 ,
,
 и
и
 найдем, воспользовавшись формулой
Бернулли:
найдем, воспользовавшись формулой
Бернулли:
 :
:

 ;
;

 ;
;
 .
.
Ряд распределения
случайной величины
 имеет вид:
имеет вид:
|
|
|
|
|
|
|
|
|
0,027 |
|
|

Ответ:
 =0,972
=0,972
-
Непрерывная случайная величина задана плотностью распределения:

Задача 4. Непрерывная случайная величина задана плотностью распределения:

Найти
коэффициент
 ,
функцию распределения
,
функцию распределения
 ,
вероятность
,
вероятность
 .
.
Дано:

Найти:
 =?
=?
 =?
=?
 =?
=?
Решение:
Используем
для нахождения а:


 ,
,



 ,
,

Найти
коэффициент
 ,
функцию распределения
,
функцию распределения
 ,
вероятность
,
вероятность
 .
.
-
Эксперты негосударственного пенсионного фонда предполагают, что на протяжении ближайших пяти лет эффективная годовая процентная ставка будет равна
 .
На протяжении следующего пятилетия
ожидается годовая процентная ставка
.
На протяжении следующего пятилетия
ожидается годовая процентная ставка
 .
Человек покупает десятилетнюю ренту
с выплатой в конце каждого года 18 000
тнг. Подсчитайте ее стоимость.
.
Человек покупает десятилетнюю ренту
с выплатой в конце каждого года 18 000
тнг. Подсчитайте ее стоимость.
Решение:




A=66522,795+6073,47=72596,269
11.Используя таблицу смертности, вычислить:
-
Вероятность того, что 30-летняя женщина доживет до 75 лет.
-
Вероятность того, что 28-летний мужчина умрет в возрасте от 40 до 45 лет.
-
Вероятность того, что 29-летний мужчина умрет в возрасте до 50 лет.
Решение:
а) Вероятность для женщины возраста 30 лет дожить до 75 лет равна:


75
b)
 =83344
=83344


c) Вероятность для мужчины возраста 29 лет умереть в возрасте до 50 лет равна :



12.Рассмотрим двух мужчин в возрасте 35 и 52 лет и 35-летнюю женщину. Найти вероятность того, что 35-летний мужчина и женщина, прожив 20 лет, умрут в течение следующих 10 лет, а 52-летний мужчина не умрет на протяжении тех же 10 лет.
Решение:
Мужчины: 87934;
87934;


 ;
;


Женщина: ;
;


13.
37% людей из числа умирающих в возрасте
от 25 до 75 лет умирают, не достигнув 50
лет. Вероятность того, что 25-летний
умрет, не достигнув 50 лет, равна 12%. Найти

Решение:
1-0.37=0.63 Люди от 25-75 лет, которые не умирают в возрасте 50 лет.
1-0,12=0,88 Вероятность того, что 25 летний не умрет, не достигнув 50 лет.
 =0.716
=0.716
14.Используя данные таблицы смертности, и предполагая равномерное распределение смертей в течение года найти:
-
Вероятность того, что 37-летний мужчина проживет 10 лет, но умрет в течение следующих трех месяцев.
Решение:



t/4

10/


У нас:
x=k+u,
где k=45
и u=

Получаем:
10/

Ответ: 0,00367
-
Вероятность того, что женщина после выхода на пенсию умрет на протяжении пяти месяцев.
15.Кривая
смертей имеет вид

 Найти:
Найти:
-
функцию выживания
 ;
; -
дисперсию времени жизни
 .
.
А)
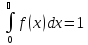

1,2347A=1; A=0,8081

16.Кривая
смертей имеет вид
 Найти функцию выживания
Найти функцию выживания
 .
.
Решение:


Ответ:

17.Интенсивность
смертности задана формулой
 .
Найти функцию выживания
.
Найти функцию выживания
 .
.
Дано:
 .
.
Найти:

Решение:


18.Функция
выживания задана формулой
 .
Найти вероятность смерти человека в
возрасте 37 лет в течение ближайших 10
лет.
.
Найти вероятность смерти человека в
возрасте 37 лет в течение ближайших 10
лет.
Решение:
Вероятность того, что он умрет течение ближайших 10 лет


19.Время
жизни некоторого конкретного человека
в возрасте 32 лет описывается законом
де Муавра с предельным возрастом
 лет. Найти вероятность того, что этот
человек проживет еще по крайней мере
20 лет.
лет. Найти вероятность того, что этот
человек проживет еще по крайней мере
20 лет.
Функция
выживания
 в модели Муавра с предельным возрастом
в модели Муавра с предельным возрастом
 имеет вид
имеет вид



20.Функция
выживания задана формулой
 .
Найти вероятность того, что человек в
возрасте 35 лет проживет еще по крайней
мере 20 лет.
.
Найти вероятность того, что человек в
возрасте 35 лет проживет еще по крайней
мере 20 лет.
21.Женщина
в возрасте 37 лет приобрела пожизненную
страховую ренту, предусматривающую
ежегодные выплаты в размере 35000 тенге,
начиная с возраста 55 лет. Эффективная
процентная ставка
 .
Найти стоимость полиса.
.
Найти стоимость полиса.
X=40 лет Р=100.000руб
i=5%
m|äX= – стоимость пожизненной ренты
– стоимость пожизненной ренты
Р=100.000 m|äX
Женщина N50=111444
D40=13372,61
50|
ä40= =8,334
=8,334
P=100000*8,334=833375,0853
22.Женщина
в возрасте 29 лет покупает страховую
ренту с ежемесячными страховыми выплатами
в размере 400 д.е., начиная с возраста 56
лет. Она намеревается оплатить стоимость
полиса посредством ежегодных премий,
уплачиваемых в начале каждого года в
течение 18 лет. Найти величину ежегодных
нетто-премий, если эффективная процентная
ставка
 .
.
23.Мужчина в возрасте 35 лет приобрел полис пожизненного страхования в размере 750000 тенге, с выплатой в конце года смерти. Стоимость полиса он будет оплачивать посредством серии платежей в начале каждого года в течение всей своей жизни. Найти размер ежегодных взносов.
Px=
750.000* 35
35
 35=
35=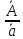 =
= *
*
M35=3357,295
N35=397183,1
 35=
35= *
* =
= =
0,008662
=
0,008662
P=7796,1282
24.Мужчина
в возрасте 50 лет заключил договор
страхования. Найти актуарную современную
стоимость пятилетней временной
пожизненной ренты, выплачиваемой раз
в год в конце года в размере 370000 тенге.
Эффективная годовая процентная ставка
 .
.
Решение:
 ;
; ;
;
 ;
;

Актуарная современная стоимость временной пожизненной ренты, выплачиваемой раз в год в начале года для суммы в одну денежную единицу равна
 ,
,
где
 – коэффициент дисконтирования.
– коэффициент дисконтирования.
 =
= ;
;

+ =
= =3,7297
=3,7297
Р =370 000*3,7369=1379997.85
25.Мужчина
в возрасте 33 лет покупает за 550000 тенге
пожизненную ренту (пенсию), выплаты
которой начинаются с возраста 60 лет.
Эффективная процентная ставка
 .
Найти величину ежемесячных выплат.
.
Найти величину ежемесячных выплат.
Решение:
Искомая
величина ежегодных выплат равна
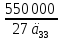
где
 – актуарная современная стоимость
пожизненной отложенной ренты.
– актуарная современная стоимость
пожизненной отложенной ренты.

Тогда величина ежегодных выплат равна.

26.Женщина
в возрасте 35 лет приобрела пожизненный
страховой полис, по которому в случае
ее смерти наследники должны получить
800000 тенге. Эффективная процентная ставка
 .
Найти стоимость полиса.
.
Найти стоимость полиса.
27.Родители
шестилетней девочки приобрели полис
по оплате получения ребенком высшего
образования по достижению им 18 лет. Срок
обучения 6 лет, стоимость 800 000 тенге в
год. Эффективная процентная ставка
 .
Найти величину ежемесячных взносов.
.
Найти величину ежемесячных взносов.
Решение:
Искомая
величина ежегодных взносов равна 600
00012|
 ,
,
где
 – величина ежегодного взноса для
отложенной срочной ренты.
– величина ежегодного взноса для
отложенной срочной ренты.
12|
 =
= =
=
28.Страхователь (мужчина) в возрасте 55 года заключил договор страхования жизни сроком на 10 лет (норма доходности – 6%). Найти ежегодную нетто-ставку в процентах (%).
Решение:
Р55:10= или 3,862%
или 3,862%
29.Страхователь (женщина) в возрасте 45 лет заключает договор страхования на дожитие сроком на 15 лет (норма доходности – 8%, страховая сумма – 450 000 тенге). Найти величину ежегодных взносов.










