Понятие о геодезическом и астрономическом азимутах

Астрономическим азимутом направления МK называют угол между северным направлением астрономического меридиана точки наблюдения М и наблюденным направлением МK.

Астрономические широты, долготы и азимуты на земной поверхности могут быть определены из наблюдений звезд.

Геодезическим азимутом А направления МK (рис.2.1) (на земной поверхности) или mk (на эллипсоиде) называют угол между северным направлением геодезического меридиана РmР' точки наблюдения и направлением МK, отредуцированным на поверхность эллипсоида. Геодезический азимут отсчитывают по ходу часовой стрелки от северного направления меридиана, от 0⁰ до 360⁰.

Геодезический азимут может быть получен двумя путями:

1. путем передачи азимутов по сторонам геодезической сети, пользуясь исходным азимутом в начальной ее точке, полученным при ориентировании референц-эллипсоида, и углами сети;

2. путем определения астрономического азимута и получения затем геодезического азимута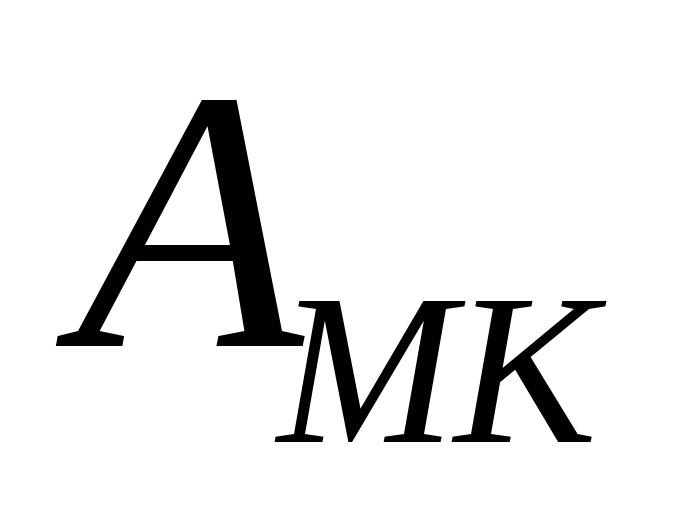направленияMK по формуле

, (2.1)

где — геодезическая и— астрономическая долготы точкиМ; — астрономическая широта точкиМ ; и— редукционные поправки в направлениеMK за перенос его с земной поверхности на поверхность референц—эллипсоида, причем — поправка за уклонение отвесной линии от нормали к эллипсоиду в точкеM, а — поправка за высоту визирной цели в точкеK над поверхностью эллипсоида. Формулы для вычисления этих малых поправок, учитываемых при высокоточных измерениях, будут даны в лекции, посвященной математической обработке результатов угловых наблюдений.

Геодезический азимут, полученный по формуле (2.1), называют азимутом Лапласа. Геодезический пункт, на котором были определены астрономический азимут и долгота, называют пунктом Лапласа, а поправочный член — поправкой Лапласа.

Геодезические координаты В, L и астрономические координаты ,не совпадают между собой вследствие несовпадения в каждой точке Земли направлений нормали и отвесной линии. Сопоставление астрономических и геодезических координат позволяет вычислить астрономо - геодезические уклонения отвесных линий, т.е. угол между нормалью к эллипсоиду и отвесной линией в данной точке.

Система прямоугольных пространственных координат (OXYZ) отнесена к центру О земного эллипсоида (рис. 2.3).

Рис. 2.3. Система прямоугольных пространственных координат ОХУZ.

Е₀ — точка пересечения Гринвичского меридиана с земным экватором.

Ось OZ располагается на полярной оси эллипсоида ; ось ОХ — в плоскости экватора и начального (Гринвичского) меридианаРЕ₀;

ось ОУ — в плоскости экватора, но в меридиане РK, плоскость которого составляет с плоскостью Гринвичского меридиана угол в .

Данная система координат приобретает все большее значение в геодезии в связи с широким внедрением в практику геодезических работ так называемых спутниковых измерений.

Система плоских прямоугольных координат (х, y).

В странах бывшего Союза общегосударственная система координат принята в проекции Гаусса – Крюгера, которая получается путем проецирования точек земной поверхности на боковую поверхность цилиндра и развертывании ее в плоскость. Такой метод дал возможность разделить всю поверхность Земли на равновеликие по площади участки, ограниченные меридианами и имеющие протяжение по широте от Северного полюса до Южного (рис.2.4).

Зоны 1 2 3 4 5 6 7

Рис. 2.4. Изображение координатных зон на плоскости в проекции Гаусса-Крюгера

Под плоскими прямоугольными координатами Гаусса понимают систему прямоугольных координат, в которой за начало координат в 6- или 3 - градусной зонах принята точка пересечения дуги осевого меридиана зоны с дугой экватора. За ось абсцисс x принято изображение дуги осевого меридиана, за ось ординат y - дуги экватора (рис.2.5). Слева от условной записи ординат подписывается номер зоны.

Рис.2.5. Система плоских

прямоугольных координат

в проекции Гаусса

Действительные значения Условные записи

ординат ординат (используемые на практике )

y = +152833,5 м (пятой зоны) y= 5 652833,5 м

y = - 127893,6 м (седьмой зоны) y= 7 372106,4 м