529

А и В, параллельно плоскости. Тогда по соображения симметрии

можно считать, что напряженности постоянны во всех точках

каждого из оснований SI и S2 по численному значению равны друг

другу и равны искомой напряженности Е в точке А. Рассчитаем

поток напряженности через рассматриваемую цилиндрическую

поверхность. Поток через боковую поверхность равен нулю, так

как линии напряженности параллельны боковой поверхности.

Следовательно, полный поток N складывается из потоков N1 И N2

через основания цилиндра SI и S2. Оба эти потока положительны.

Так как поверхности SI и S2 перпендикулярны к линиям

напряженности, то потоки через них получаются умножением

величины напряженности на площадь основания. Таким образом

имеем:

N=N1+N2=E'SI+E'S2=2 ЕВ.

По теореме Остроградского - Гаусса полный поток должен равняться произведению 1/ео на заряд, заключенный внутри

поверхности. Следовательно,

2 ЕВ = cr S / ео

откуда искомая напряженность Е получается равной

Значение Е не зависит от расстояния точки А от плоскости То же относится и к точке В. Таким образом, мы получаем справа и слева

от UЛОСКОСТИ однородные поля. Если плоскость заряжена

отрицательно, то направление напряженности противоположно

-разобранному: линии будут входить в плоскость. Полученный результат только для бесконечной плоскости, так как только в таком случае могут быть использованы приведенные соображения

симметрии, однако приближенно он справедлив для пространства,

прилегающего к средней части Конечной плоскости, вдали от ее

краев.

21

www.mitht.ru/e-library

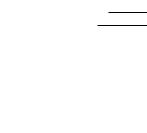
2. Поле двух бесконечных параллельных плоскостей,

+

Рис. 3.

Линии напряженности поля

двух параллельных плоскостей,

заряженных разноименными

зарядами с плотностями

+о" И -<J.

Решение можно получить непосредственно геометрическим

сложением полей двух плоскостей, заряженных разноименно. Из

рис. 3 видно, что напряженности полей обеих плоскостей между

плоскостями направлены в одну сторону следовательно, их

геометрическая сумма является их арифметической суммой.

Напряженность поля каждой плоскости, согласно предыдущему равна cr/2f,o, следовательно, полная напряженность между

Напряженности, создаваемые обеими плоскостями правее правой

левее левой плоскостей, направлены в противоположные стороны.

Следовательно, их геометрическая сумма равна разности их

численных значений; так как численное значение напряженности,

создаваемой каждой плоскостью, равно 21tcr, то результирующая

напряженность для точек вне плоскости равна нулю

Е=О. (4а)

3.Напряженность поля, создаваемоrо равномерно заряженной сферической поверхностью. Предположим, что сферическая

поверхность радиуса R заряжена положительным электричеством

и что поверхностная плотность заряда +о" постоянна во всех точках

поверхности. Общий заряд сферической поверхности обозначим через q. Задачу разобьем на две части: а) определение напряженности электростатического поля вне сферической поверхности, б) определение напряженности внутри сферической

поверхности.

22

www.mitht.ru/e-library

Рис. 4.

К определенЕПО напряженности

поля заряженной сферы.

Возьмем точку А, отстоящую от центра заряженной сферической

поверхности на расстоянииr r>R (рис. 29). Проведем через нее

мысленно сферическую поверхность S радиуса r с центром в

центре заряженной сферы. По соображениям симметрии ясно, что

напряженность будет численно равна во всех точках этой

поверхности. Также по соображениям симметрии ясно, что в каждой точке вектор напряженности должен быть направлен по

перпендикулярна к линиям напряженности, то полный поток через

нее получим, умножив напряженность Е на величину поверхности,

откуда полный поток равен Ео 4mJ.

По теореме Остроградского-- Гаусса имеем

Е ~'4Jff'2= ,. 4/Sо

т. е. напряженность, создаваемая равномерно заряженной

сферической поверхностью, вне нее такая же, как если бы весь

заряд нахQдuлся в ее центре.

Перейдем к точкам, лежащим внутри сферической поверхности.

Возьмем точку В (рис. 29), отстоящую от центра сферы на расстоянии r<R И проведем через эту точку сферическую поверхность S' с центром в центре заряженной сферы. Очевидно,

23

www.mitht.ru/e-library

что напряженности во всех точках этой поверхности будет

численно одинакова.

Так же, как и выше, по соображениям симметрии ясно, что напряженность (если она отлична от нуля) может иметь только

радиальное направление и, следовательно, перпендикулярна к

сферической поверхности S'. Применяя теорему Остроградского

- Гаусса к сферической поверхности S',получим

Е/'fш,2= О,

так как внутри поверхности S'заряд равен нулю; отсюда:

Следовательно, напряженность электростатического поля во

всех точках внутри равномерно заряженной сферической

поверхности равна нулю.

Можно показать (ер. § 132), что формулы (5) и (6) остаются справедливыми и для заряженного проводящего шара с зарядом q.

4. Напряженность поля, создаваемого равномерно заряженной

сферой. Возьмем сферу радиуса R, общий положительный заряд q которой распределен по объему сферы с постоянной плотностью

р- q - q

- v - 43 тcR3

Напряженность поля в произвольной точке А (рис. 29), находящейся вне заряженной сферы и отстоящей от центра сферы

на расстоянии r>R, очевидно, дается тем же выражением, что и напряженность от заряженной сферической поверхности:

q

Е=-- r 2

и направлена так же по продолжению радиуса, так как

соображения симметрии и расчет будут здесь те же. Таким

образом, равномерно заряженная сфера в точках вне ее создает

www.mitht.ru/e24-library

такую наnря.женность, как если бы весь ее заряд был

сосредоточен в центре.

Определим напряженность в точке В, лежащей внутри

заряженной сферы и отстоящей от центра сферы на расстоянии r<R. В этом случае условия симметрии те же, что и выше, откуда

следует, что напряженность численно одинакова на всех точках

сферической поверхности радиуса r' с центром в центре

заряженной сферы, причем в каждой точке напряженность имеет

радиальное направл~ние. Заряд q', находЯЩИЙСЯ внутри

п,)верхности радиуса [', равен:

a'=p~7l:r'3

. 3

а

или, так как р:::; _.--'~ ":;;',го

; ;rr:R J

ИЗ ФОРМУЛЫ (7) ВИДНО, ЧТО l-/f:l1РЯ;)II'еЮ{ОСI:n, 61Iутри равномерно

заряженной сферы возрастает nроnорцион(!,'lЬНО расстоянию от

центра сферы. Это оБСТОЯТСЛf,СТВО vОУСЛОЕЛI;НО тем фактом, что

напряженность создается лишь той ЧCtСТЬЮ общего заряда, которая отстоит от центра не дальше, чем та точка, в которой вычисляется

напряженность. Следовательно, чем дальше от центра берется

точка, тем больший заряд создает в ней напряженность.

25

www.mitht.ru/e-library

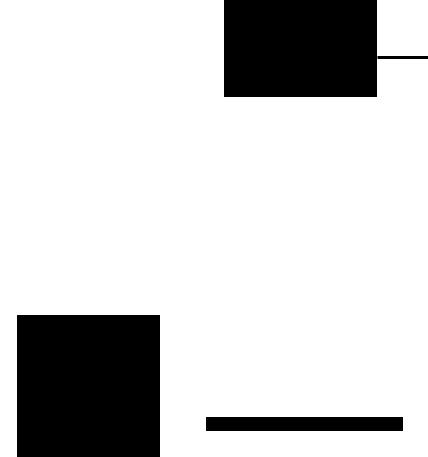
r

.:феры; б - объемно заряженной сферы,

5. Напряженность поля, со,щаваеМОJ'О равномерно заlНlжеllНОЙ f,ес~онсчной ЦИ.iшндрическоЙ НОЬЧ>ХifО(ТLЮ. Возьмем

1.iР!ПШllр!iческую поверхность ра)щуса Н. '3ilРЮ1,'енную с i~';(·1"('ЯШ-Юй. поверхностной плотно(тью -- (1, Определим

!j;tЛ;)1Iiкеш'ость В точке А, m~тоящсй Н,. р~,,-,:т()янии (>R от оси i~::ЛШДР3 (рис. 31). Симмеrрия 'Цl:ачи (1"':;"::, ЛОЧЮ;I9.ет :заключитr"

1::'1"(\ H:-\НРЯ'.Кt'нно(::ь в точке А до;т.ка::: 01ТР. вапрзвлена по

!.j~'~,'Д('ЛЖ-':НПЮ раДИУС<l-вектора r.

Рис, 6.

К (\ПРl::,·.-:iеннКJ !1апряж~ш,юсти

П'-JВ~РХНОСТИ, ось которой совnада~г (; ()с!,"-..; заряжеННQГО

цилиндра. а верхнее и нижнее Оt:нования llсрпендикулярны

у оси и отстоят друг от друга на рас,;,:тоянни 1. Полный

поток через эту поверхность выразится тольк() потоком

через боковую поверхность, так как напряженность

параллеJlьна основаниям, и поток через них равен нулю.

Так как линии напряженности перпендикулярны к боковой

26

www.mitht.ru/e-library

поверхности цилиндра, то мы получим полный поток N, умножая

значение напряженности Е на величину боковой поверхности 21lГZ:

В силу теоремы Остроградского-- Гаусса, поток численно равен произведению 4н на заряд, заключенный внутри поверхности,

через которую рассчитывается поток; этот заряд равен заряду,

приходящемуся на длину 1 цилиндра:

q=(1 '21l R /,

сравнивая это выражение для N с выражением (8), получим:

2н&о r

Так как 2JrR численно равно площади боковой поверхности цилиндра, отнесенной к единице длины цилиндра, то ч=2JrR(1 представляет собой заряд, отнесенный к е,динице длины цилиндра, Отсюда формуле (9) может быть также придан вид:

'7

Е=-- (9а) 2нво r

Наnряженuость поля убывает обратно nРОnОРЦИOJ.lа7ЫIO

расстоянию от оси цилиндра. Аналогичным приемом легко

показать, что наnряж'енность поля внутри paeHO;"tepHO

заряженной ЦWIU1lдрической поверхностиравна uулю. Рассмотренные приемы показывают, что применение теоремы Остроградского Гаусса дает возможность рассчитать

электростатичёское поле в тех случаях, когда оно симметрично, и

по соображения r симметрии можно наперед указать направление

линий напряженности.

27

www.mitht.ru/e-library