
Расчет теплообменных аппаратов с различной структурой потоков
.pdf
4. Расчет теплообменных аппаратов с различной структурой потоков.
4.1. Основы теплопереноса.
В основе расчета теплообменников лежит основное уравнение теплопередачи
Q=k∆срF |
(4.1) |
Где Q – тепловой поток (Вт), k – коэффициент теплопередачи (Вт/(м2К), ∆ср – средняя (по поверхности) движущая сила процесса теплопередачи (К), F - поверхность теплопередачи (м2).
Тепловой поток зависит от расходов теплоносителей G1 и G2, их теплоемкостей с1 и с2 и температур на входе Т′ и t′ и на выходе Т′′ и t′′:
Q=G1c1(T′-T′′)=G2c2(t′′-t′) |
(4.2) |
В выражении (4.2) произведения G1c1 и G2c2 – пропускные способности стадий подвода и отвода теплоты, соответственно.
Коэффициент теплопередачи от одного теплоносителя к другому через плоскую стенку толщиной δст и теплоемкостью λст зависит также от коэффициентов теплоотдачи α1 и α2 по обеим сторонам теплопередающей поверхности.
|
|
|
|
|
|
|
(4.3) |
|
|
|
ст |
|
|
|
|
|
|
|
|
||||
|
|
|
ст |
|
|||
домножив на F правую и левую части (4.3), получим |
|
||||||
|
|
|
|
ст |
(4.3а) |
||
|
|
|
|
|
|||
|
|
|
|
|
ст |
|
|
где kF – пропускная способность стадии теплопередачи α1F и α2F – пропускные способности стадий теплоотдачи, λстF/δст – пропускная способность стадии теплопроводности через стенку.
Результирующая пропускная способность стадии теплопередачи (kF), естественно, зависит от пропускных способностей отдельных стадий и всегда меньше наименьшей из них .
При расчете необходимой поверхности теплообменника (проектная задача) уравнение (4.1) решают относительно F и по найденной величине подбирают стандартный теплообменник.
Влияние структуры потоков теплоносителей на эффективность работы теплообменника удобнее проследить на примере эксплуатационной задачи. Эксплуатационные задачи рассматривают ситуации, когда известны потоки теплоносителей и их температуры на входе в аппарат Т′ и t′, а также параметры, определяющие интенсивность теплопереноса между теплоносителями. Для задач эксплуатации выражение (4.1) безусловно, остается справедливым, но для расчета теплового потока Q оно не может быть прямо использовано, так как известны лишь входные температуры. На выходе из теплообменника температуры Т′′ и t′′ не заданы, поэтому величину ∆ср найти нельзя (исключение - теплообмен между конденсирующимся паром и кипящей жидкостью, когда ∆ср = Т′–t′ известна по условиям процесса). В таких ситуациях методику расчета Q целесообразно основывать на разности входных температур теплоносителей ∆*= T′- t′.
Последовательно найдем тепловые потоки Q для некоторых простейших случаев.
4.2. Тепловой поток при движении теплоносителей в режиме идеального перемешивания.
Эта технологическая ситуация в расчетном плане — одна из самых простых. Рассмотрим теплообменник (рис. 4.1), в котором оба теплоносителя
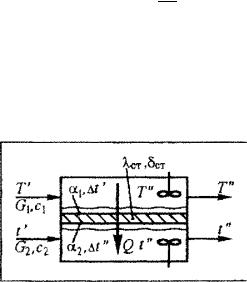
движутся (без изменения агрегатного состояния) в режиме идеального перемешивания (символ ИП, на рисунке — мешалки). Поэто му температуры в теплообменнике каждого теплоносителя — постоянны по поверхности теплообмена и равны таковым на выходе Т′′ и t′′. Подлежащи й последующему переносу к холодному теплоносителю поток т еплоты Q, вносимый с горячим теплоносителем (его пропускная способность G1c1), последовательно проходит через тепловой пограничный слой с горячей стороны (пропускная сп особность α1F), стенку (Fλст/δст), пограничный слой с холодной стороны (α2F) и уносится холодным теплоносителем (пропускная способность G2c2), Запи шем выражения для Q применительно ко всем отдельным стадиям:
(a)
причем θ1 и θ2 — температуры стенки (здесь постоянные вдоль F ) со стороны горячего и х олодного теплоносителей соответств енно.
Рис. 4.1 Расчетная схема эксплуатационной задачи при идеальном смешении теплоносителей.
Решим равенства (а) относительно частных разност ей температур и исключим все промежуточные температуры , оставив лишь известные T′ и t′:

−=
−=
−−="(=ст ст)
−= 
Сложим почленно правые и левые части. |
|
|
|
|
|
||||||||||||
− ≡ ∆ = ( |
1 |
+ |
1 |
+ |
( ст 1ст) |
+ |
1 |
+ |
1 |
) |
|||||||
Отсюда получается выражение для искомого потока теплоты: |
|||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.4) |
||
|
|
|
( ст ст) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Или в более лаконичной записи, если все (три) поверхностные
стадии теплопереноса объединить в одну стадию теплопередачи: |
|
|||||
= |
|
|
|
|
|
(4.5) |
|
|
|
|
|
||
Для большей общности с последующим изложением перепишем |
||||||
(4.5), подставив слагаемые в знаменателе правой части в форме |
|
|||||
безразмерных комплексов путем домножения на kF и знаменателя и |
|
|||||
числителя = |
( |
) |
|
= |
∆ |
(4.6) |
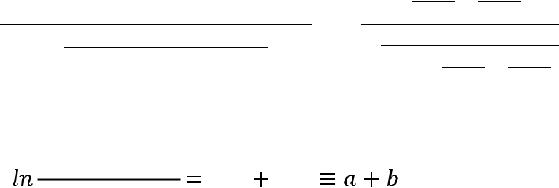
где символами a=kF/(G1c1) и b=kF/(G2c2) обозначены отношения пропускных способностей поверхностной с отдельных потоковых стадий теплообмена.
4.3 Тепловой поток при прямоточном и противоточном движении теплоносителей.
В случае прямоточного движения обоих теплоносителей (без изменения агрегатного состояния) в режиме идеального вытеснения температуры T и t изменяются вдоль F так, что анализ несколько усложняется. Выражения для Q с записью стадий теплопередачи (в целом) принимают вид:
Q=G1c1(T′-T′′)=kF∆ср=G2c2(t′′-t′) (б)
Чтобы исключить из конечных формул не известные заранее
температуры T′′ и t′′, выразим их из первого и последнего равенств (б): |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= |
− |
|
|
|
, |
|
|
|
|
|
= |
+ |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
и подставим в среднее равенство (б), раскрывая написание ∆ср: |
|||||||||||||||||||||||||||||||||
= |
( |
− |
) − ( |
|
|
− |
|
|
|
|
− ( + |
|
|
|
|
)) |
= |
( |
11 |
1 |
+ |
21 2 |
) |
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
− ′ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆ |
|
|
|
|
|||||
|
|
|
|
|
|
− |
|
|
|
− ( + |
|
|
|
) |
|
|
|
|
|
∆ − ( |
11 1 |
+ |
21 2 |
) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
Отсюда после сокращения на Q (при этом Q под знаком ln остается) |
|||||||||||||||||||||||||||||||||
|
|
|
∆ |
( |
|
∆ |
|
|
|
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(г) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
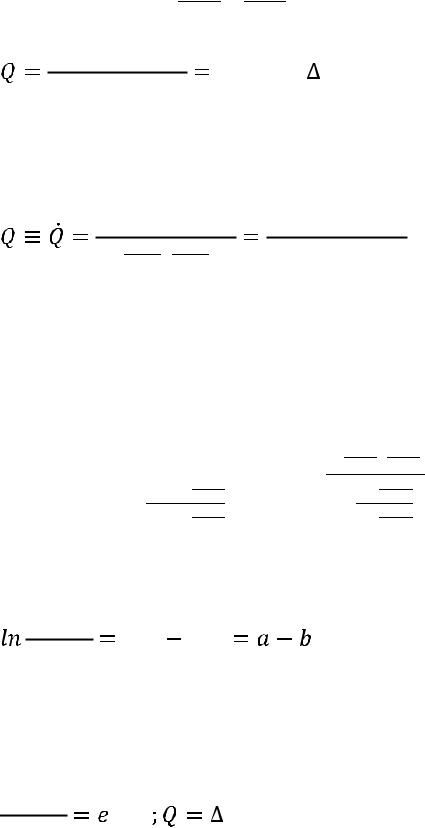
Потенцируем и разрешаем полученное равенство относительно искомого потока теплоты:
|
|
|
|
|
∆ |
|
|
|
|
|
) = |
|||
|
∆ − ( |
|
11 1 |
+ |
21 |
2 |
||||||||
( ( |
|
)∆ |
) |
|
|
|
( |
|
|
) |
|
|
||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||||
Как и в случае ИП, знаменатель (4.7) можно привести к
безразмерному виду, домножив его (числитель тоже) на kF. |
|||
∆ ( |
( )) |
∆ ( |
( )) |
(4.7)
(4.8)
В случае противоточного движения теплоносителей в режиме ИВ
(и также без изменения агрегатного состояния) остаются справедливы равенства (б), но ∆ср формируется по-иному . Подставим значения T′′ и t′′ в
выражение ∆ср для противотока:
=  = ( )
= ( )
|
Отсюда (после сокращения на Q) |
|
|
|
|
|
||||||||||
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
(д) |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
∆ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Потенцируем и разрешаем полученное равенство относительно |
|||||||||||||||
искомого потока теплоты: |
|
|
|
|
|
|
|
|
|
|||||||
|
∆ |
|
|
|
|
|
|
( ) |
|
(4.9) |
||||||
|
|
|
|
|
||||||||||||
|
∆ |
|
|
|
|
|
|
|
|
) |
||||||
|
|
|
|
|
|
|
|
( |
|
|||||||
|
|
|
|
|
|
|
|
|||||||||
Или с безразмерными комплексами в знаменателе:
|
(( |
)) |
(4.10) |
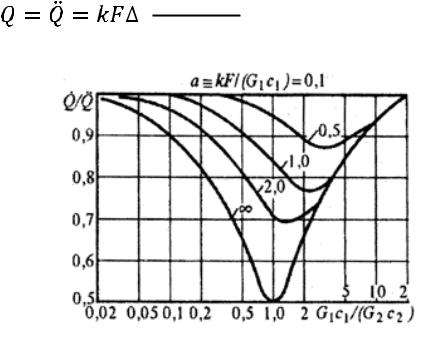
Рис. 4.2 Сравнительная интенсивность теплопереноса при прямотоке и противотоке в задачах эксплуатации.
Заметим, что в случаях прямотока и противотока из (4.8) и (4.10)
легко найти пропускные способности теплообмена в целом Q/∆* . |
|
̈ |
и |
Полученные выражения для потоков теплоты при прямотоке |
|
противотоке позволяют провести их сопоставление в условиях |
̇ |
эксплуатационной̇/ ̈ задачи теплообмена. На рис. 4.2 показана зависимость от (G1c1)/(G2с2) = b/a, при различных kF/(G1 c1 ) = а. Можно
констатировать, что при очень малых и очень больших значениях комплекса (G1c1)/(G2с2), а также при малых kF/(G1c1) прямоток и противоток в аспекте интенсивности теплопереноса равноценны. Это объясняется, малым изменением в указанных условиях температуры одного из теплоносителей вдоль теплообменной поверхности: например, согласно равенству (б), при (G1c1)/(G2с2) →0 очевидно t ≈ const (поскольку t ′′ - t'→ 0); соответственно при (G1c1)/(G2с2) →∞ будет Т ≈ const; наконец,
при kF/(G1c1) → 0 получается (Т' – T′′)/∆ср→ 0, т.е. опять-таки Т ≈ const. А при постоянстве температур одного из теплоносителей взаимное
направление их потоков перестает сказываться на интенсивности |
|
||||||||
теплообмена. Однако при сопоставимости значений G1c1, G2с2 и kF |
|
||||||||
|
|
|
|
|
|
|
/ |
|
|
интенсивность теплопереноса для прямотока всегда ниже, чем для |
|
||||||||
противотока: на рис. 4.2 в этом случае |
|
< 1, причем при G1c1 = G2с2 и kF |
|
||||||
̈ |
|
- |
|
|
|
|
показать и путем прямого деления |
|
|
>> G1c1 , G2с2 |
|
ровно вдвое. Это легко |
̇ ̈ |
̇ |
|||||
на с последующими предельными переходами - сначала с учетом а = b, а |
|||||||||
затем a→∞. |
|
|
|
|
|
|
|
|
|
|
Аналогичным способом получаются выражения для Q , если один |
|
|||||||
из теплоносителей движется в режиме ИВ, а другой — в режиме ИП. Надо |
|
||||||||
только соответственно записать выражение для среднелогарифмического |
|
||||||||
напора ∆ср. Еще проще получить формулу для Q, если один из потоков |
|
||||||||
изменяет агрегатное состояние. Например, в случае конденсации пара надо |
|
||||||||
учесть постоянство температуры Т = Т′ = const, приняв пропускную |
|
||||||||
способность этой стадии бесконечно большой: как бы G1c1→∞. Тогда а = |
|
||||||||
kF/(G1c1), и выражения (4.8) и (4.10) превращаются в более простое: |
|
||||||||
|
= |
∆ |
|
|
|
|
|
|
|
|
̈ |
|
|
|
|
|
|
(4.11) |
|
|
|
|
|
|
|
||||
Наконец, если оба теплоносителя изменяют агрегатное состояние, то проще всего воспользоваться выражением (4.5),
положив в нем G1c1, G2с2 →∞ или (4.6) с учетом a, b→0.
Тогда
Q=kF∆* |
(4.1), (4.6) |
Т.е. при изменении агрегатного состояния обоих теплоносителей задачи эксплуатации и проектирования применительно к отысканию ∆ср совпадают, поскольку температуры вдоль всей поверхности теплообмена заданы T=T′, t=t′ – и постоянны, а ∆* = ∆ср.
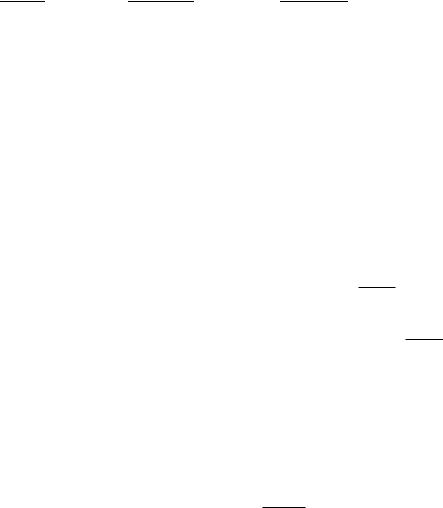
Для ряда более сложных схем движения теплоносителей (смешанные токи; движение теплоносителей в режимах, промежуточных между ИВ и ИП, и др.) также получены [м] выражения для Q.
Из выражений (4.6), (4.8), (4.10) легко получаются значения
средних температурных напоров – путем сопоставления с (4.1) для |
|
||||
рассматриваемых случаев соответственно: |
(( |
)) |
|
||
∆ср= ∆ |
; ∆ср= ∆ |
( ) ; ∆ср= ∆ |
(е) |
||
Для сложных схем движения теплоносителей тоже могут быть найдены выражения, связывающие ∆ср и ∆* с помощью пропускных способностей (a и b).
Пример Т 1. Сравнение эффективности теплообменников с различной структурой потоков.
В теплообменнике поверхностью F = 10 м2 потоком горячей воды G1
= 2,00 кг/с при температуре Т’=900С (ее теплоемкость с1 = 4,19 кДж )
кг × К
нагревается поток жидкости G2 = 4,00 кг/с с теплоемкостью с2 = 3,84
поступающей в теплообменник при температуре t ‘=200C.
Сравнить тепловые нагрузки теплообменника с различной структурой потоков теплоносителей и их температуры на выходе, приняв
одинаковым коэффициент теплопередачи k= 1200 .
Решение.
В основе расчета лежат следующие формулы (4.6), (4.8) и (4.10)
Располагаемая разность температур:
D* = T '-t'= 90 - 20 = 700 C .
Отношения пропускных способностей стадии теплопередачи (kF) и отдельных потоковых стадий теплообмена G1∙c1 и G2∙c2:
a = |
|
k × F |
= |
1200 ×10 |
=1,432 , |
||
|
G1 × c1 |
2 × 4,19 ×103 |
|||||
|
|
|
|
|
|
||
b = |
|
k × F |
|
= |
1200 ×10 |
|
= 0,781. |
G2 × c2 |
|
4 × 3,84 ×103 |
|
||||
|
|
|
|
|
|||
Для случая идеального перемешивания (ИП) обоих теплоносителей:
* |
1 |
|
1 |
|
5 |
Вт, |
||
Q = k × F × D |
× |
|
=1200 ×10 × 70 × |
|
|
= 2,62 ×10 |
|
|
a + 1 + b |
1,432 + 1 + 0,781 |
|
||||||
Q =262 кВт.
Температура горячего теплоносителя на выходе из теплообменника
равна:
T '' = T '- |
|
Q |
= 90 - |
|
262 |
= 58,70 C . |
|
G |
|
× c |
2 |
× 4,19 |
|||
|
|
|
|
||||
|
1 |
1 |
|
|
|
|
|
Температура холодного теплоносителя на выходе из теплообменника равна:
t'' = t'+ |
Q |
= 20 + |
|
262 |
= 20 +17,1 = 37,10 C . |
|
G2 × c2 |
4 |
× 3,84 |
||||
|
|
|
При прямотоке в режиме ИВ (расчет по формуле 4.8):
∙ |
* |
1 - e−(a+b) |
|
1 - е−(1,432+0,781) |
|
5 |
Вт, |
|
Q = k × F × D × |
|
=1200 ×10 × 70 × |
|
|
= 3,38 ×10 |
|
||
a + b |
1,432 + 0,781 |
|
||||||
∙
Q =338 кВт.
