
Законы электростатики
..pdfМосковская государственная академия тонкой химической технологии имени М.В. Ломоносова
Законы электростатики
МОСКВА 2010
Оглавление |
|
§ 1. Электростатическое поле в вакууме................................................................................................... |
3 |
Контрольные вопросы ................................................................................................................................ |
4 |
Задачи с решениями .................................................................................................................................... |
4 |
Задачи для самостоятельного решения ................................................................................................... |
10 |
§ 2. Диэлектрики и проводники в электрическом поле ....................................................................... |
11 |
Задачи с решениями .................................................................................................................................. |
11 |
Задачи для самостоятельного решения ................................................................................................... |
16 |
§ 3. Электроемкость. Энергия электрического поля.............................................................................. |
16 |
Задачи с решениями .................................................................................................................................. |
17 |
Задачи для самостоятельного решения ................................................................................................... |
25 |
ЛИТЕРАТУРА........................................................................................................................................... |
26 |
2

§ 1. Электростатическое поле в вакууме
Закон Кулона: Сила взаимодействия между точечными зарядами q1 и q1, находящимися на расстоянии r в среде с диэлектрической проницаемостью :
F |
|
q1q2 |
|
, |
|
||
4 |
0 |
r 2 |
|
||||
|
|
|
|
|
|
||
где 0 - электрическая постоянная. |
|
||||||
Напряженность поля |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
||
|
E |
|
|
|
. |
|
|
|
|
|
q |
|
|
||
|
|
|
|
|
|||
|
|
|
|
|
|
||
Связь между напряженностью E и электрическим смещением D : |
|||||||
|
|
|
|
|
|
||
D |
|
0 E . |
|
|
|
||
Напряженность поля точечного заряда, а также поля вне равномерно заряженного шара или сферы:
E |
|
q |
|
. |
|
|
|
||
4 |
0 |
r 2 |
||
|
|
|
|
Напряженность поля вне равномерно заряженного цилиндра на расстоянии r от его оси:
E 2 0 r ,
где  - заряд единицы длины цилиндра.
- заряд единицы длины цилиндра.
Напряженность поля плоскости, равномерно заряженной с поверхностной плотностью :
E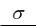 . 2 0
. 2 0
Напряженность поля в плоском, цилиндрическом и сферическом конденсаторах:
E |
|
; E |
|
|
|
; E |
|
q |
|
. |
|
|
|
|
|
|
|
||||
|
2 |
0 |
r |
4 |
0 |
r 2 |
||||
0 |
|
|
|
|
|
|
|
|||
Работа электрического поля по переносу заряда q из точки 1 в точку 2:
A qU ,
где U – разность потенциалов между точками 1 и 2.
Связь между напряженностью E и разностью потенциалов |
1 |
||
|
|
|
|
2 |
|
|
|
1 2 Ex dx; Ex |
|
. |
|
|
|
||
1 |
x |
|
|
Потенциал поля точечного заряда, а также поля вне заряженного шара или сферы на расстоянии R от центра:
q . 4 0 R
3
2 :
равномерно
Контрольные вопросы
1.Что называется силовыми линиями электростатического поля? Могут ли они пересекаться?
2.Является ли электростатическое поле потенциальным?
3.Что называется эквипотенциальной поверхностью?
4.Сформулируйте принцип суперпозиции для напряженности и потенциала.
5.Объясните принцип действия электроскопа.
Задачи с решениями
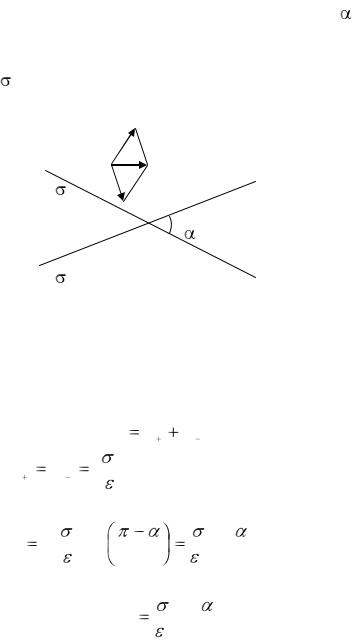
Задача 1. Две пересекающиеся под углом бесконечные плоскости делят пространство на четыре области. Чему равна напряженность электрического поля в областях 1 и 2, если поверхностные плотности зарядов плоскостей + 
и - ? |
|
|
E+ |
|
1 |
+ |
E- |
|
2 |
- |
|
|
Рис. 1.1. |
Решение:
В области 1 напряженность поля согласно принципу суперпозиции
электрических полей равна векторной сумме напряженностей полей, |
|||||||||||||
созданных каждой из плоскостей в отдельности: |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
E E , |
(1) |
|
где |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||
|
E |
|
|
|
E |
|
|
|
|
|
|
||
|
|
|
|
|
2 |
0 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
Следовательно, для модуля вектора напряженности имеем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
E |
|
2 |
|
cos |
|
|
|
|
|
|
|
|
|
sin |
|
. |
(2) |
|
|
|
2 0 |
2 |
|
|
|
|
0 |
2 |
||||||||||
|
|
|
|
|
|
|
|||||||||||||
В области 2 напряженность поля равна |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
(3) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
E |
|
|
|
|
cos |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
0 |
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 2. В вершинах квадрата с диагональю 2l находятся точечные заряды q и –q, как показано на рис. 1.2.
4
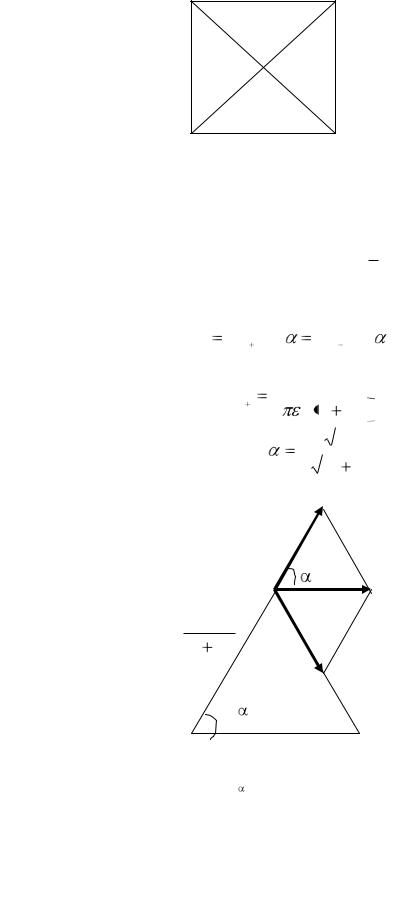
Найти модуль вектора напряженности электрического поля в точке, отстоящей на расстояние x от центра квадрата и расположенной симметрично относительно вершин квадрата.
+ q |
+ q |
- q |
- q |
Рис. 1.2.
Решение:
Точка наблюдения является вершиной пирамиды, основанием которой
является квадрат со стороной 
 2l / 2 .
2l / 2 .
Рассмотрим левую боковую грань, содержащую заряды + q и – q. Напряженность поля, созданного этими зарядами, равна
E1 2E cos |
|
2E cos |
, |
(1) |
||||||
где напряженность поля от одного заряда |
|
|||||||||
E |
|
|
q |
|
|
|
, |
(2) |
||
|
|
|
|
|
|
|
||||
4 |
0 |
l 2 |
|
x2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos |
|
|
|
|
2l |
|
. |
(3) |
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
2 |
|
l 2 |
|
x2 |
|||||
|
|
|
|
|
|
|
||||
E+
E1

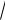 l 2 x2
l 2 x2
E-
+ q |
- q |
Рис. 1.3.
5

Вторая пара разноименных зарядов дает такую же напряженность E1 . Искомый модуль напряженности поля, созданного всеми четырьмя зарядами, равен
E 2E1 |
|
|
|
ql |
|
. |
(4) |
|
|
|
|
|
|||
|
|
|
l 2 |
x2 3 / 2 |
|||
2 |
0 |
||||||
|
|
|
|
|
|
|
Задача 3. На расстоянии h от бесконечной плоскости находится точечный заряд +q. Определить напряженность поля в точке А, отстоящей от плоскости и от заряда на расстояние h (см. рис.1.4.(а)).
Рис. 1.4. а) |
Рис. 1.4. б) |
Решение.
Для решения этой задачи удобно использовать «метод изображений». Потенциал бесконечной заряженной плоскости равен 0. Заменим эту задачу другой задачей, поместив по другую сторону от плоскости заряд (-q) и убрав мысленно плоскость (см. рис. 1.4.(б)).
В любой точке В, ранее принадлежавшей плоскости, потенциал попрежнему
|
q |
( |
q) |
0 . |
(1) |
||
В |
|
|
|
|
|||
4 0 r |
4 |
0 r |
|||||
|
|
|
|||||
Таким образом, в верхнем полупространстве (над плоскостью) граничные
условия для потенциала остались теми же, и таким же |
осталось поле в этой |
|||||||||||||||||||||||||||||||||||||
области. |
Тогда |
|
напряженность электрического поля |
в |
точке А равна |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
векторной сумме |
напряженности |
поля |
Е1 , созданной |
зарядом (+q), и |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
напряженности Е2 |
, созданной зарядом |
(-q). По теореме косинусов |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Е |
|
|
Е 2 |
|
|
Е 2 |
|
|
2Е Е |
2 |
cos . |
|
|
|
|
|
|
(2) |
|
|
|||||||||||||||||
|
|
|
|
|
1 |
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
С другой стороны, из прямоугольного треугольника КАL |
|
|||||||||||||||||||||||||||||||||||||
|
cos |
|
KA |
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
1 |
|
. |
|
|
|
|
(3) |
|
|
||||||||||
|
AL |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
h2 |
2h 2 |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Напряженности полей, созданных точечными зарядами q и (-q) , равны |
||||||||||||||||||||||||||||||||||||||
Е1 |
|
q |
|
|
, |
|
|
|
|
|
Е2 |
|
|
|
|
|
|
q |
|
|
|
|
q |
(4) |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4 |
0 h2 |
|
|
|
|
|
|
4 |
|
|
|
0 AL2 |
4 |
|
0 5h2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
q |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
E |
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
26 2 |
5 .(5) |
|
|
||||||||||||||
|
|
0 h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 h2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
4 |
|
|
|
|
|
|
25 |
|
|
5 |
|
|
5 20 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|

Задача 4. Имеются два тонких проволочных кольца радиуса R каждое, оси которых совпадают. Заряды колец равны q и q . Найти разность
потенциалов между центрами колец, отстоящими друг от друга на расстояние a .
q
a
- q
Рис. 1.5.
Решение:
Найдем сначала потенциал поля, созданного одиночным заряженным кольцом в точке наблюдения, лежащей на оси кольца на расстоянии r от его центра.
Разобъем кольцо на элементарные отрезки длиной dl и несущие заряд dq. Потенциал поля от элементарного заряда dq в точке на расстоянии r от центра кольца равен
d |
|
|
dq |
|
|
. |
(1) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|||||
4 |
0 |
|
R2 |
r 2 |
|
|||
|
|
|
|
|
|
|
|
|
Интегрируя (1) по всему кольцу, находим потенциал поля, созданного всем кольцом на расстоянии r от центра:
|
|
q |
|
|
. |
(2) |
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|||
4 |
0 |
R2 |
r 2 |
|
||
|
|
|
|
|
|
|
Используя (2) и принцип суперпозиции для потенциала, найдем потенциал в центре верхнего и нижнего кольца соответственно:
|
q |
|
q |
|
|
, |
(3) |
||
1 |
|
|
|
|
|
|
|
||
4 0 R 4 |
|
|
|
|
|||||
|
|
|
|||||||
|
R2 |
a2 |
|
||||||
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
7
|
q |
|
q |
|
|
. |
(4) |
||
2 |
|
|
|
|
|
|
|
||
4 0 R 4 |
|
|
|
|
|||||
|
|
|
|||||||
|
R2 |
a2 |
|
||||||
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
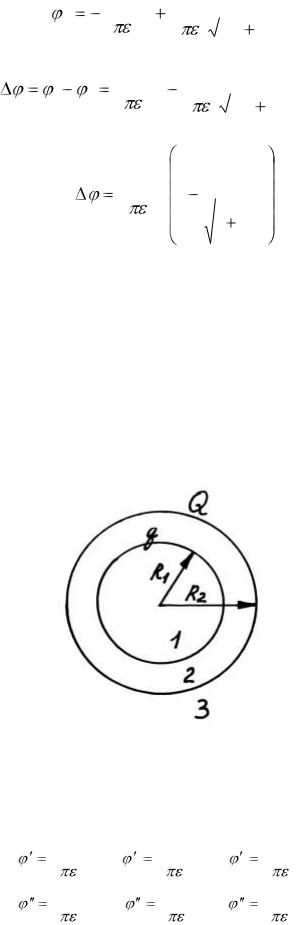
Следовательно, разность потенциалов между центрами колец равна
|
|
q |
|
q |
|
|
. |
(5) |
||
1 |
2 |
|
|
|
|
|
|
|
||
2 0 R 2 |
|
|
|
|
||||||
|
|
|
||||||||
|
R2 |
a2 |
|
|||||||
|
|
0 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
q |
1 |
|
|
1 |
|
|
|
. |
|
|
|
|
|
|
||||
2 0 R |
|
|
|
|
|
||||
1 |
|
a2 |
|
||||||
|
|
|
|
R2 |
|||||
|
|
|
|
|
|
||||
Задача 5. Система состоит из двух концентрических проводящих сфер, причем на внутренней сфере радиусом R1 находится заряд q, на внешней сфере радиусом R2 находится заряд Q. 1. Найти потенциал электрического поля во всем пространстве.
2. Каким должен быть заряд Q, чтобы потенциал внутренней сферы был равен 0? Нарисовать примерный график зависимости потенциала φ от расстояния до центра системы для этого случая, считая q<0.
Решение.
Рис. 1.6.
Воспользуемся принципом суперпозиции. Пусть 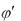 - потенциал, созданный только сферой R1 ,
- потенциал, созданный только сферой R1 ,  - потенциал, созданный только сферой R2 . Тогда в областях 1, 2, 3 соответственно (см. рис.)
- потенциал, созданный только сферой R2 . Тогда в областях 1, 2, 3 соответственно (см. рис.)
- 33 -
|
|
q |
, |
|
|
|
q |
, |
|||
1 |
|
|
2 |
|
|
|
|
||||
4 |
0 R1 |
4 |
0 r |
||||||||
|
|
|
|
|
|||||||
|
|
Q |
|
, |
|
|
|
Q |
, |
||
1 |
|
|
|
2 |
|
|
|
|
|||
4 |
0 R2 |
|
4 |
0 R2 |
|||||||
|
|
|
|
|
|||||||
|
|
q |
|
|
, |
(6) |
3 |
|
|
|
|
||
|
|
|
|
|||
|
4 |
|
0 r |
|
||
|
|
Q |
|
. |
(7) |
|
3 |
|
|
|
|||
|
|
|
||||
|
4 |
|
0 r |
|
||
|
|
|
8 |
|
||
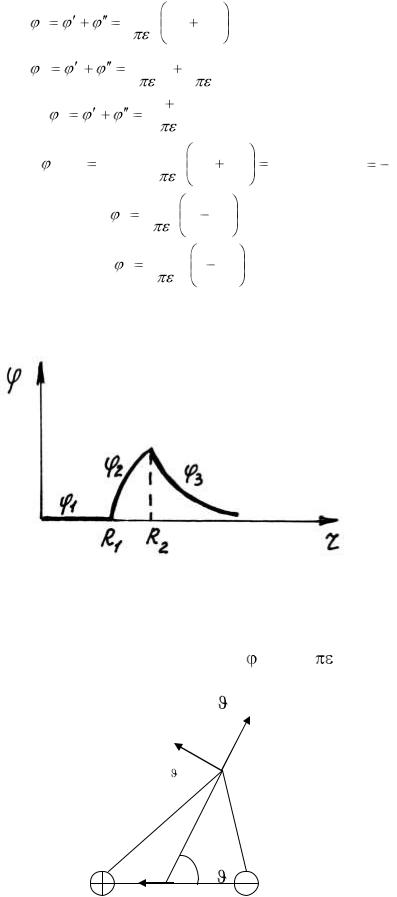
Тогда |
|
|
|
|
1 |
|
|
|
|
q |
|
|
|
Q |
|
|
, |
|
|
(8) |
|
|
|||||||||
1 |
1 |
1 |
4 |
|
|
|
|
|
R1 |
|
|
R2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
q |
|
|
|
|
|
|
|
|
|
Q |
|
|
|
|
|
|
|
(9) |
|
|
||||
|
2 |
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
0 r |
4 |
|
|
0 R2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
(q |
|
Q) |
. |
|
|
|
|
|
|
|
|
(10) |
|
|
||||||||||
|
|
3 |
3 |
3 |
|
4 |
|
0 r |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2. Если |
|
(R ) |
0 |
, то |
1 |
|
|
|
|
|
|
q |
|
|
|
Q |
0 , откуда Q |
qR2 |
. Тогда |
||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 |
|
|
|
|
4 |
|
|
|
|
|
|
|
R1 |
|
|
R2 |
|
R1 |
||||||||||||
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
q |
1 |
|
|
|
1 |
|
, |
|
(11) |
|
|
|||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
4 |
|
|
0 r |
|
|
|
R1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
q |
1 |
|
R2 |
. |
(12) |
|
|
||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
4 |
|
|
0 r |
|
|
|
|
R1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
График зависимости φ(r) для этого случая показан на рисунке.
Рис. 1.7.
Задача 6. Показать, что потенциал поля диполя с электрическим моментом p может быть представлен как = pr /4 0 r3 , где r – радиус-вектор. Найти с помощью этого выражения модуль вектора напряженности электрического поля диполя как функцию r и .
|
|
|
Er |
|
E |
|
|
|
r+ |
r- |
|
+ q |
- |
- |
- q |
|
|
9

Рис. 1.8.
Решение:
Потенциал электрического поля диполя в точке наблюдения на расстоянии r+ от положительного заряда и r- от отрицательного заряда равен
q |
|
q |
|
|
|
|
|
. |
(1) |
4 0 r |
4 0 r |
|||
Учитывая, что длина диполя l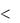 r, находим расстояния от зарядов диполя до точки наблюдения:
r, находим расстояния от зарядов диполя до точки наблюдения:
r r |
l cos |
, r r |
l cos |
. |
(2) |
|
|
|
|||||
2 |
2 |
|||||
|
|
|
|
Подставляя (2) в (1), получаем потенциал поля диполя:
|
|
|
|
|
|
|
|
|
|
|
|
pr |
|
, |
(3) |
|
|
4 |
0 |
r 3 |
|||
|
|
|
|
|
|
||
где |
|
|
|
|
|||
p |
ql - электрический момент диполя. |
|
|||||
Радиальная компонента вектора напряженности поля равна
Er |
|
|
p cos |
. |
(4) |
|||
|
|
|
|
|
||||
r |
2 |
0 |
r 3 |
|||||
|
|
|
||||||
|
|
|
|
|
|
|
||
Перпендикулярная (поперечная) компонента напряженности
|
|
|
p sin |
|
|||
E |
|
|
|
|
|
. |
(5) |
r |
4 |
0 |
r 3 |
||||
|
|
|
|
|
|
|
|
Модуль вектора напряженности электрического поля
|
|
|
|
|
p |
|
|
|
|
|
E E 2 |
E 2 |
|
|
1 3cos2 . |
(6) |
|||||
|
|
|
||||||||
|
r |
4 |
|
r 3 |
|
|
|
|
||
|
|
0 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Задачи для самостоятельного решения
1.Электростатическое поле создается шаром радиусом R = 0,10 м,
равномерно заряженным с объемной плотностью = 20 нКл/м3 . Определите разность потенциалов между точками, лежащими внутри шара на расстояниях r1 = 2 см и r2 = 8 см от его центра.
Ответ: |
1 |
2 |
|
|
r 2 |
r 2 |
= 2,26 В. |
|
|
||||||
|
6 |
2 |
1 |
|
|||
|
|
|
0 |
|
|
|
|
2. В вершинах квадрата со стороной a = 5 см находятся одинаковые положительные заряды Q = 2 нКл.
Определите напряженность электростатического поля: 1) в центре квадрата; 2) в середине одной из сторон
квадрата.
Ответ: 1) E1 = 0; 2) |
E2 |
|
4Q |
|
|
= 10,3 кВ/м. |
|
|
|
|
|
|
|||
|
|
|
|
a 2 |
|||
5 |
5 |
|
0 |
||||
|
|
|
|
||||
|
|
|
|
|
|
|
10 |
