ГВЕЛЕСИАНИ,ШЕЛОНИН-Основные особенности и параметры зонной структуры полупроводников (2010)

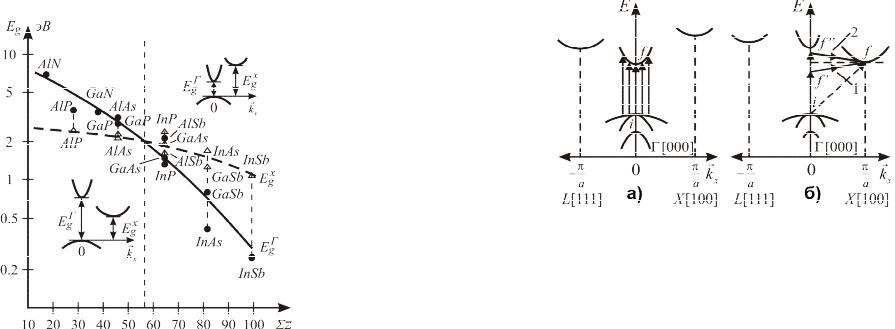
Формула Р. Бьюба дает достаточно хорошо согласованный результат с величинами экспериментальных значений Eg , за исключением очень малых и очень больших

значений Z , т.к. зависимость Eg от них нелинейная.

Интерес представляет раздельное рассмотрение зависимостей «прямой» запрещенной зоны Eg и «непрямой»

EgX от суммарного заряда ядра в соединениях AIIIBV (рис.6.3).

Рис.6.3. Зависимость ширины прямой Eg и непрямой EgX

запрещенных зон от суммарного заряда ядра соединений типа AIIIBV.

С увеличением ΣZ происходит монотонное опускание дна зоны проводимости, приводящее к уменьшению Eg ,

причем скорость уменьшения «прямой» запрещенной зоны

42

вектору и согласно закону сохранения импульса записывается как:

перехода в зону проводимости, а Pi , ki – в валентной зоне до воздействия фотона.

Рис.5.2. Прямые и непрямые оптические переходы электронов из валентной зоны в зону проводимости. а – прямые переходы; б – непрямые переходы с поглощением (1) и испусканием (2) фононов.

Для совершения переходов с изменением импульса электрона необходимо, кроме фотона, участие третьей частицы, способной передать электрону необходимые импульсы. Такой частицей чаще всего является фонон. Причем при передаче импульса от фонона возможно

поглощение или испускание фонона (рис.5.2.б). Под воздействием фотона электрон совершает прямой переход i f ' или i f '', а затем под воздействием фонона непрямой

испусканием фонона.

31

С учетом поглощения или испускания фонона, закон сохранения импульса записывается в виде:

где Pq , q – импульс и волновой вектор фонона.

Оптические переходы электронов без изменения

значений P или k называются прямыми, а с изменением – непрямыми. Очевидно, что вероятность непрямых переходов значительно меньше, чем прямых и, следовательно, непрямозонные полупроводники значительно слабее, чем прямозонные, поглощают или излучают энергию света.

6. Фундаментальные параметры зонной структуры полупроводников

1.Eg – ширина запрещенной зоны энергии,

энергетический интервал между главными экстремумами зоны проводимости и валентной зоны. Чем больше величина Eg , тем ярче выражены полупроводниковые свойства.

2. Eg – ширина запрещенной зоны энергии для прямых

переходов электронов (без изменения k ) в непрямозонном полупроводнике.

3.Es – интервал энергии между нижайшей и

следующей подзоной зоны проводимости.

4. – величина спинорбитального расщепления в валентной зоне – интервал энергии между экстремумом отщепленной подзоны и главным экстремумом валентной зоны. (при спинорбитальном взаимодействии происходит смещение зон с различным направлением спина относительно друг друга, из-за того, что различным направлениям спина в магнитном поле соответствует разная энергия).

32

механической прочностью через удельную поверхностную энергию ε111:

запрещенной зоны был предложен Р. Бьюбом. Этот расчет основан на анализе большого числа экспериментальных данных величин запрещенных зон полупроводниковых соединений. Р. Бьюб предложил эмпирическую формулу:

Eg CVB VA ,

Z

где C 43 – эмпирический коэффициент; VB , VA – валентности компонентов B и A соединения, Z – суммарный заряд соединения.

41

величиной. Коэффициент q учитывает природу химической связи и является функцией разности электроотрицательностей (для соединений) Χ, эффективных зарядов компонентов соединений qэфф. и атомного номера (заряда ядра Z).

Увеличение Z ослабляет ковалентную связь, а увеличение Χ и qэфф увеличивает прочность смешанной ковалентно-ионной связи.

С учетом ковалентной, ионной и металлической связи коэффициент q можно записать в виде:

(6.8)

где С, М, Р – условные величины, характеризующие степень влияния ковалентной, металлической и ионной связи, которые

разность электроотрицательностей, qэфф – коэффициент пропорциональности, который учитывает величины эффективных зарядов атомных остатков А+δ, В-δ, рост которых в ряду соединений приводит к усилению асимметрии амплитуд потенциального поля кристалла и увеличению Eg .

Эмпирически установлено, что величина Eg (при

прочих равных условиях) пропорциональна отношению чисел валентных электронов VA и VB в некоторой степени n.

Для расчета Eg в электрон-вольтах Б.Ф. Ормонтом были предложены несколько уравнений, одно из которых:

40

электронов и дырок. (индекс d от английского density – плотность).

полупроводников, являются эффективная масса и ширина запрещенной зоны.

6.1. Свойства эффективной массы

1.От величины эффективной массы с одной стороны зависят динамические свойства (подвижность) электронов и дырок в электрическом поле и при диффузии, с другой стороны – плотность разрешенных состояний в зонах и другие статистические параметры полупроводников.

2.От величины эффективной массы зависит форма зон

коэффициенты пропорциональности.

Кривизну функции E k характеризует 2-ая производная энергии электрона (дырки) по волновому

33

3. Так как k – вектор, то 2-ая производная является тензором 2-го ранга (совокупность 9-ти частных производных 2-го порядка) и определяет тензор обратной эффективной массы, а обратный ему тензор есть тензор эффективной массы:

Таким образом, в общем случае, эффективная масса анизотропна (зависит от направления движения электрона относительно кристаллографических осей). В изотропных кристаллах – скалярная величина.

Соответствующим выбором осей координат тензор можно привести к диагональному виду, в котором отличны от нуля только диагональные члены:

4. Величина и знак эффективной массы зависит от величины и знака обменного интеграла энергии:

34

где λ=0 для IV гр., λ=1 для AIIIBV, λ=2 для AIIBVI.

Наличие в полупроводниковых соединениях, наряду с ковалентной, некоторой доли ионной связи, зависящей от разницы электроотрицательностей компонентов соединения, приводит к упрочнению химической связи и увеличению Eg .

В приближении квазисвободного электрона увеличение Eg

соединений с повышением доли ионной связи объясняется усилением асимметрии электронного облака и соответственно увеличением разницы между максимумом и минимумом периодического потенциала кристалла, что и ведет к увеличению запрещенной зоны. При равных Z и Z Eg

соединений существенно больше, чем у простых полупроводников (см. рис.6.2).

6.3. Теоретический расчет ширины запрещенной зоны

Приведенный ниже расчет Eg был предложен

Б.Ф. Ормонтом.

По Б.Ф. Ормонту энергетическую прочность химической связи и соответственно величину запрещенной зоны в ковалентных кристаллах точнее всего можно выразить через энергию атомизации кристалла Ω. Действительно, чем прочнее связи между атомами, тем больше энергии необходимо для перевода электрона из валентной зоны в зону проводимости:

где q – коэффициент, который имеет одинаковое значение,

только для полупроводников в пределах своих групп: IV гр., AIIIBV и AIIBVI. При переходе от полупроводников IV гр. к AIIIBV и AIIBVI коэффициент q быстро растет. Это значит, что

Eg зависит не только от прочности, но и характера химической связи, т.е. является связечувствительной

39

В приближении квазисвободного электрона

(периодический потенциал учитывается как малое возмущение) увеличение Eg с уменьшением Z и размеров

электронного облака объясняется более резким изменением между максимумом и минимумом периодического потенциала в кристалле.

В ряду простых полупроводников: кремний, германий, серое олово, как и в ряду соединений аналогов, по мере увеличения заряда ядра (атомного номера) увеличивается длина связи валентных электронов с ядром, ковалентная связь слабеет и наблюдается переход к гомеополярной металлической связи. Экспериментально установлено, что значения Eg и длины связей d удовлетворяют условию:

Впростых полупроводниках кристаллический потенциал UIV(r) симметричен по отношению к перестановке двух соседних атомов.

Вполупроводниковых соединениях, из-за отсутствия

инверсионного центра симметрии, кристаллический потенциал содержит антисимметричную часть UA(r):

где λ – мера антисимметричной части кристаллического потенциала.

В изоэлектронных рядах (равное количество электронов на атом): Si-Si(Z=14)-AlP(14); Ge-Ge(32)- GaAs(32)-ZnSe(32); αSn(50)-InSb(50)-CdTe(50), каждое соединение можно представить как образованное из соединений IV-IV путем замены атомов IV гр. соседним из III

иV групп, или II и VI групп.

Сучетом асимметричной части кристаллического потенциала запрещенную зону можно выразить как:

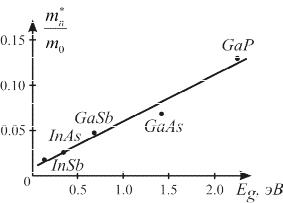
5. Эффективная масса электронов, в пределах определенной группы полупроводников, прямо пропорциональна величине запрещенной зоны Eg. У полупроводников с небольшой Eg небольшая величина mn и

наоборот. Подвижность квазисвободных электронов, следовательно, почти обратно пропорциональна ширине запрещенной зоны.

Рис.6.1. Зависимость величины эффективной массы электронов от ширины запрещенной зоны

в ряду соединений AIII BV .

35

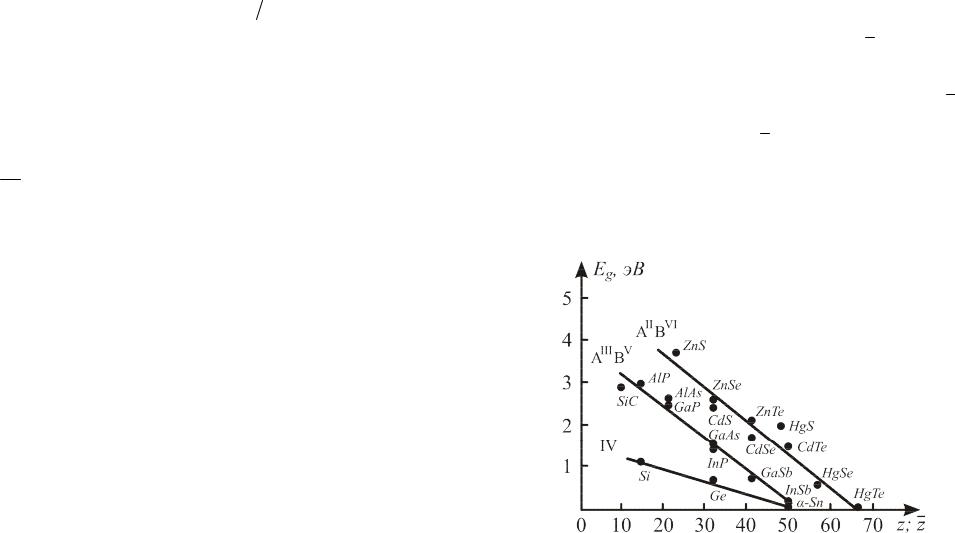
Таблица 6.1.

Эффективная масса электронов в -минимуме монотонно возрастает с увеличением «прямой» запрещенной зоны:

mn 0.05Eg . m0

Эффективная масса дырок с ростом Eg изменяется сравнительно слабо: от 0.45m0 для InSb (Eg=0,18 эВ) до 0,9m0

для GaP (Eg=2,26 эВ).

6. Эффективная масса имеет размерность массы покоя электрона, измеряют ее как долю этой массы, по величине она может быть как меньше, так и больше массы покоя, например mn =0,02m0, или mn =1,08m0.

6.2. Анализ величины запрещенной зоны энергии

Ширина запрещенной зоны – один из важнейших параметров полупроводников, от которого зависят электрические и оптические свойства полупроводников. Области применения полупроводников во многом связаны с величиной запрещенной зоны. Например, для полупроводниковых приборов, работающих в области высоких температур, высоковольтных приборов, светодиодов видимого диапазона требуются широкозонные полупроводники; для низковольтных приборов, фотоэлектрических приборов, принимающих или излучающих низкие энергии, требуются узкозонные полупроводники.

36

Величина запрещенной зоны определяется структурой внешних электронных оболочек полупроводника и зависит от заряда ядра атома Z в пределах группы простых полупроводников или от среднего заряда ядра Z в пределах группы соединений аналогов.

В приближении сильной связи электрона с атомом уменьшение ширины запрещенной зоны с ростом Z или Z объясняется увеличением обменного интеграла энергии.

Чем больше Z или Z , тем больше размеры электронного облака и степень перекрытия электронных оболочек соседних атомов, тем интенсивнее обмен электронами, больше величина обменного интеграла энергии и связанная с ним ширина разрешенных зон энергии, соответственно меньше величина запрещенной зоны.

Рис.6.2. Зависимость величины запрещенной зоны от заряда ядра простых полупроводников и среднего заряда ядра полупроводниковых соединений типа AIIIBV и AIIBVI.

37