
ГВЕЛЕСИАНИ,ШЕЛОНИН-Основные особенности и параметры зонной структуры полупроводников (2010)
.pdf
Министерство образования и науки Российской Федерации
Московская государственная академия тонкой химической технологии им. М.В. Ломоносова
Кафедра физики и химии твердого тела
Гвелесиани А.А., Шелонин Е.А.
Основные особенности и параметры зонной структуры полупроводников
Учебное пособие
2010
http://www.mitht.ru/e-library
ББК Г25 22.37 |
|
|
|
Издание учебное |
|
|
УДК 539.21 |
|
|
Рецензент |
|
|
|
|
|
|
|
|
|
|
к.т.н., доц. Батырев Н.И. (МИТХТ, кафедра материалов |
Гвелесиани Александр Александрович |
|||||
микро-, опто- и наноэлектроники) |
|
|
Шелонин Евгений Александрович |
|||
|
Гвелесиани А.А., Шелонин Е.А. |
|
|
|
||
|
Основные особенности и параметры |
|
Учебное пособие |
|
||
|
зонной структуры полупроводников. |
|
Под редакцией |
|
||
|
Учебное пособие |
|
|
д.т.н., проф. Яковенко Анатолия Георгиевича |
||
|
М.: МИТХТ им. М.В. Ломоносова, 2010. |
|
|
|||
|
71 с., таблиц 1, илл. 27. |
|
|
|
|
|
|
Утверждено Библиотечно-издательской комиссией |
|
|
|||
МИТХТ им. М.В. Ломоносова в качестве учебного пособия. |
Подписано в печать |
Формат 60х84/16 |
||||
Поз. |
/2010. |
|
|
|
Бумага писчая |
|
|
Данное учебное пособие является дополнением к курсу |
Отпечатано на ризографе. Уч. изд. листов |
||||
лекций по дисциплине «Физика и химия твердофазных |
Тираж 100 экз. |
|
||||
систем», читаемых для студентов, обучающихся по |
Заказ № |
|
||||
образовательной |
программе |
бакалавриата |
551600 |
|
|
|
«Материаловедение и технология новых материалов», и |
|
|
||||
может быть также полезным для студентов специалитета и |
|
|
||||
магистратуры. |
|
|
|
|
|
|
|
В пособии изложены основные представления об |
|
|
|||
особенностях и фундаментальных параметрах зонной |
Московская государственная академия тонкой химической |
|||||
структуры полупроводников, дана классификация зонных |
технологии им. М.В. Ломоносова |
|||||
структур, анализируются величины эффективных масс |
|
|
||||
электронов и дырок, ширина запрещенной зоны. Даны |
|
|
||||
представления об одномерной и трехмерной зонной структуре |
Издательско-полиграфический центр. |
|||||
полупроводников. |
|
|
|
119571, Москва, пр. Вернадского, 86. |
||
|
Данное учебное пособие должно способствовать более |
|
|
|||
глубокому пониманию студентами подходов к созданию |
|
|
||||
новых и модернизации традиционных полупроводников. |
|
|
||||
|
|
© МИТХТ им. М.В. Ломоносова |
|
|
||
|
|
2 |
|
|
|
71 |
http://www.mitht.ru/e-library
Рекомендуемая литература
1.Шалимова К.В. Физика полупроводников. Учебник для ВУЗов. М.: Энергоатомиздат, 1985 – 392с.
2.Фистуль В.И. Введение в физику полупроводников. Учебное пособие. М.: Высш. шк., 1984 – 352с.
3.Займан Дж. Принципы теории твердого тела. Пер. с
англ. М.: Мир, 1966 – 416с.
4.Ормонт Б.Ф. Введение в физическую химию и кристаллохимию полупроводников. М.: Высш. шк., 1968 – 488с.
5.Киреев П.С. Физика полупроводников. Учебное пособие для ВУЗов. М.: Высш. шк., 1975 – 584с.
6.Постников В.С. Физика и химия твердого состояния. Учебник для ВУЗов. М.: Металлургия, 1978 – 544с.
7.Зеегер К. Физика полупроводников. Пер. с англ. М.:
Мир, 1977 – 615с.
8.Горбачев В.В., Спицина Л.Г. Физика металлов и полупроводников. Учебное пособие. М.: Металлургия, 1976 – 368с.
9.Фистуль В.И. Физика и химия твердого тела. Ч. I. Учебник для ВУЗов. М: Металлургия 1995 – 320с.
10.Росадо Л. Физическая электроника и микроэлектроника. Пер с испан. Учебное пособие для ВУЗов. М.: Высш. шк., 1991 – 351с.
70
Содержание |
|
|
Введение |
5 |
|
1. |
Закон дисперсии свободных электронов в вакууме |
7 |
2. |
Закон дисперсии электронов, движущихся в кристалле |
8 |
|
2.1. Закон дисперсии электронов в кристалле |
15 |
|
в окрестности точки k 0 |
|
3. |
Образование гибридных sp3 зон энергии в кристаллах |
18 |
|
со структурой алмаза |
|
4. |
Трехмерные зоны в k -пространстве |
20 |
5. |
Особенности зонных структур полупроводников |
26 |
|
5.1. Классификация зонных структур полупроводников |
29 |
6. Фундаментальные параметры зонной структуры |
32 |
|
|
полупроводников |
|
|
6.1. Свойства эффективной массы |
33 |
|
6.2. Анализ величины запрещенной зоны энергии |
36 |
|
6.3. Теоретический расчет ширины запрещенной зоны |
39 |
|
6.4. Влияние температуры на ширину запрещенной |
43 |
|
зоны |
|
|
6.5. Влияние состава твердых растворов полупро- |
45 |
|
водников на ширину запрещенной зоны |
|
7. |
Зонная структура основных полупроводниковых |
49 |
|
материалов |
|
|
7.1. Зонная структура кремния |
51 |
|
7.1.1. Эффективная масса плотности состояний |
54 |
|
электронов |
|
|
3 |
|
http://www.mitht.ru/e-library
7.1.2 Структура валентной зоны. Эффективная |
55 |
масса плотности состояний дырок |
|
7.2. Зонная структура германия |
58 |
7.3. Зонная структура арсенида галлия |
61 |
7.4. Зонная структура антимонида индия. |
65 |
Заключение |
67 |
Рекомендуемая литература |
70 |
4
проводимости и валентной зоны) различают узкозонные и широкозонные полупроводники.
16. Различие в свойствах идеализированных (с идеальной кристаллической структурой) собственных полупроводников главным образом связано:
–с природой химической связи и типом кристаллической структуры;
–с особенностями зонной структуры (прямозонная, непрямозонная);
–с величинами запрещенных зон и эффективных масс электронов и дырок;
–с наличием в зонной структуре второго минимума энергии в зоне проводимости, разделенного небольшим интервалом энергии с абсолютным минимумом.
69
http://www.mitht.ru/e-library
прямозонного полупроводника уравнением сферы, непрямозонного полупроводника – уравнением эллипсоида вращения.
8.Чем больше величина объемного обменного интеграла энергии, тем больше ширина разрешенных зон энергии и тем меньше величина запрещенных зон.
9.Чем больше энергия дискретного уровня атома, тем шире образованная из него энергетическая зона и тем меньше запрещенная зона.
10.Эффективные массы электронов и дырок обратно пропорциональны величине обменного интеграла энергии и постоянной кристаллической решетки в квадрате.
11.В общем случае эффективная масса электронов является тензорной величиной, откуда деление эффективных масс квазисвободных электронов на продольные и поперечные.
12.Эффективные массы дырок – скалярные величины, но в валентной зоне полупроводников существуют два сорта дырок с разной величиной эффективных масс – тяжелых и легких, что связано с разной кривизной двух подзон с общим экстремумом энергии.
13.Для большинства полупроводников, имеющих алмазоподобную кристаллическую решетку, зонную структуру строят в направлениях волновых векторов вдоль осей <100> и <111>.
14.По особенностям зонной структуры (расположению абсолютного экстремума зоны проводимости относительно центра симметрии) полупроводники классифицируют на прямозонные и непрямозонные. Соответственно, различают прямые и непрямые запрещенные зоны.
15.По величине минимальной запрещенной зоны (интервал между абсолютными экстремумами зоны
68
Введение
Зонную структуру твердого тела описывают через энергию электрона в функции его волнового вектора
E kx,ky,kz .
Волновое число k является основным квантовым числом, определяющим состояние системы электронов в
кристалле, |
поэтому зависимость |
E kx,ky,kz |
имеет |
фундаментальное значение и определяет свойства твердых тел.
Значения k , в пространстве волновых векторов, ограничены размерами зон Бриллюэна. На границах зон Бриллюэна энергия электронов испытывает разрыв, вследствие чего энергетический спектр электронов в кристалле представляет собой чередование разрешенных и запрещенных зон энергии, т.е. имеет зонный характер. Таким образом, движение электронов в кристалле ограничено
размерами энергетической зоны в k -пространстве.
Для полного описания всей совокупности энергетических состояний электронов в кристалле, область
значений k достаточно ограничить элементарной ячейкой обратной решетки, т.е. одной (первой) зоной Бриллюэна.
Совокупность электронных уровней энергии,
описываемых функцией En k и ограниченных значениями k
называется энергетической зоной (n-номер зоны). Внутри зоны волновой вектор изменяется квазинепрерывно и определяет квазинепрерывный спектр состояний электронов в зонах. Таким образом, энергетическая зона состоит из подуровней энергии, а их количество равно количеству атомов N в единице объема кристалла. Интервалы между подуровнями ничтожно малы ~10-22 эВ.
5
http://www.mitht.ru/e-library

На каждом подуровне энергии находится не более 2-х электронов с разной ориентацией спина, а количество электронов в зоне равно 2N или 2gN, где g-фактор вырождения, равный для s-состояний электронов 1, а для p- состояний 3-м.
Внутри энергетической зоны изменение энергии электрона описывается функцией E k , характер зависимости которой вытекает из закона дисперсии электронов в кристалле. Такое название закона связано с волновым представлением об электроне, а именно с зависимостью частоты электронной волны от ее волнового вектора.
В настоящем учебном пособии рассматриваются зонные структуры идеализированных полупроводников, для которых кристаллическая структура считается идеальной, а потенциальное поле кристаллов строго периодическим.
6
Заключение
1. Зонную структуру полупроводников описывают функцией E k , которая изменяется квазинепрерывно в пределах энергетических зон обратной решетки и испытывает
разрывы при значениях волновых векторов электронов a
для одномерной и 2 для трехмерной обратной решетки. a
2.Обратная кристаллическая решетка строится в пространстве волновых чисел электронов и обладает всеми свойствами симметрии кристаллической решетки.
3.Трехмерную зонную структуру полупроводников с алмазоподобной кристаллической структурой, строят как элементарную ячейку Вигнера-Зейтца обратной Г.Ц.К. решетки, которая имеет форму кубоктаэдра.
4.Физической причиной образования зонного энергетического спектра электронов в кристалле является Вульф-Брегговское отражение и интерференция электронных волн.
5.Энергия квазисвободного электрона, движущегося в кристалле, ограничена пределами разрешенных зон энергии в
k-пространстве.
6.Закон дисперсии электронов в кристалле в окрестности абсолютных экстремумов зон для одномерного
k -пространства носит параболический характер, а коэффициентом пропорциональности между энергией и волновым вектором является эффективная масса электрона (дырки).
7. Законы дисперсии электронов в окрестности
абсолютных минимумов зон проводимости трехмерного k -
пространства |
E kx,ky,kz |
описываются, |
в |
случае |
|
|
67 |
|
|
http://www.mitht.ru/e-library
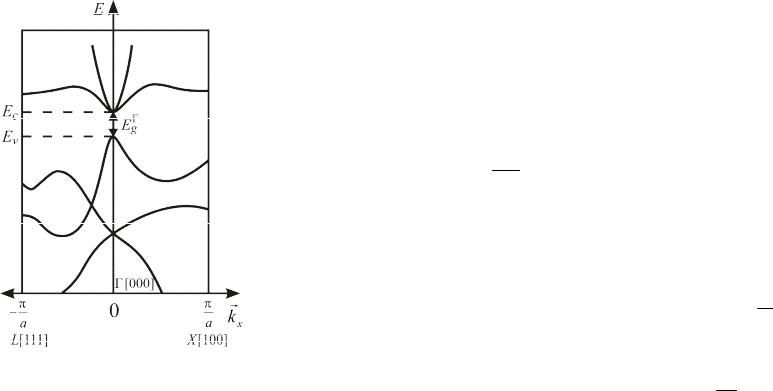
Рис.7.10. Одномерная зонная структура антимонида индия.
В валентной зоне, в области экстремумов подзон тяжелых и легких дырок, отщепленной подзоны, изоэнергетические поверхности – сферы. Эффективная масса плотности состояний для дырок mdp 0.6m0 , которая по
величине совпадает с эффективной массой тяжелых дырок.
66
1. Закон дисперсии свободных электронов в вакууме
Для свободного электрона в вакууме закон дисперсии записывается как:
|
|
|
2 2 |
|
|
E k |
|
pi |
, |
(1.1) |
|
|
|
||||
|
|
2m0 |
|
||
где pi , m0 – |
импульс и масса покоя электрона, i x, y,z; |
||||
2 – коэффициент пропорциональности между энергией и
2m0
импульсом электрона.
Электрон в вакууме движется неограниченно и обладает только кинетической энергией. Согласно де Бройлю электрону, движущемуся со скоростью v , соответствует волна, длина которой:
|
h |
|
или |
h |
. |
m v |
|
||||
i |
i |
i |
p |
||
|
0 |
|
i |
||
Так как длину волны можно выразить через волновое число k :
|
|
2 |
|
2 |
|
h |
|||
|
|
|
|
|
|
|
|
|
|
i |
k |
|
, то |
p , |
|||||
i |
k |
i |
|||||||
|
|
|
|
|
|
i |
|||
откуда импульс свободного электрона: pi ki .
Тогда закон дисперсии запишется как:
|
|
2 |
k |
2 |
|
|
E k |
|
|
|
. |
(1.2) |
|
|
|
|
||||
|
|
2m0 |
|
|||
Согласно формулам (1.1 и 1.2) закон дисперсии электрона в вакууме имеет параболический характер, его удобно изображать графически. Можно фиксировать 2 из 3-х
компонент ki , тогда зависимость (1.1) есть парабола на плоскости E kx , E ky , E kz .
7
http://www.mitht.ru/e-library
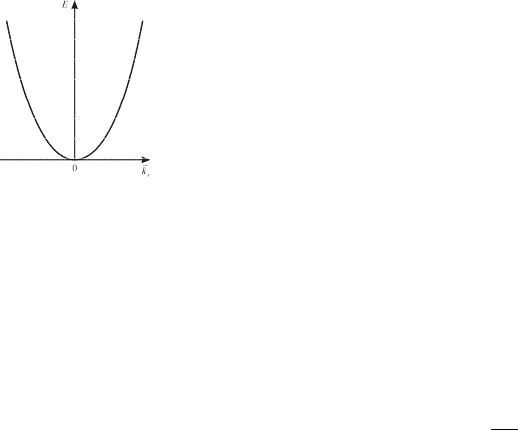
Рис.1.1. Зависимость E kx для электрона, движущегося в вакууме.
Совокупность парабол E kx , |
E ky , |
E kz полностью |
характеризует закон дисперсии. |
|
|
2. Закон дисперсии электронов, движущихся в кристалле
Ограничимся рассмотрением движения электрона в периодическом потенциальном поле простой кубической решетки, в которой каждый атом окружен шестью ближайшими атомами (Zk=6).
В кристалле электрон движется в периодическом потенциальном поле, замедляя (между атомами) или ускоряя (в области атомов) свое движение, его амплитуда изменяется с периодом кристаллической решетки (а).
Для электрона, движущегося в кристалле, можно ввести величину p k , называемую квазиимпульсом. Квазиимпульс, в отличие от импульса электрона в вакууме, изменяется, также как и волновой вектор, квазинепрерывно. Электрон в кристалле обладает и кинетической и потенциальной энергией, последняя связана с усредненным зарядом атомных ядер и электронов.
8
7.4. Зонная структура антимонида индия.
Антимонид индия InSb – типичный узкозонный, прямозонный полупроводник. Структурный тип и первая зона Бриллюэна такие же, как и у арсенида галлия. Доля ионной составляющей связи значительно меньше, чем у арсенида галлия.
Зонная структура строится в направлениях кристаллографических осей <100> и <111> (рис.7.10).
Основные особенности: небольшая величина прямой запрященной зоны, при 0 К Eg 0.24 эВ, при 300 К
Eg 0.18 эВ; сильная кривизна зоны проводимости в области
минимума энергии, вследствие чего очень малы эффективная масса электронов и плотность квантовых состояний в зоне проводимости; большая концентрация собственных носителей заряда, при 300 К ni 1016 см-3. Кроме того,
большое различие между эффективными массами электронов
mp |
46, где m |
|
0.6m , |
m |
|
0.013m , а |
||||
и тяжелых дырок |
T |
pT |
|
|||||||
|
|
|||||||||
m |
|
|
|
0 |
n |
|
0 |
|||
n |
|
|
|
|
|
|
|
|
|
|
также между эффективными |
массами |
тяжелых и |
легких |
|||||||
дырок mpT 50, где mp 0.012m0 . mpЛ Л
Изоэнергетическая поверхность в области минимума энергии зоны проводимости – сфера.
Вследствие малой величины эффективной массы электронов, а также небольшой доли ионной связи, антимонид индия отличает очень высокая подвижность электронов un 78000 см2/В·с.
65
http://www.mitht.ru/e-library
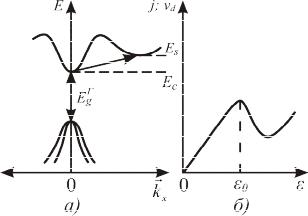
Рис.7.9. а – фрагмент зонной структуры арсенида галлия в направлении <100> (Δ);
б – зависимость дрейфовой скорости и плотности тока от напряженности сильного электрического поля
для арсенида галлия.
Зависимость дрейфовой скорости и плотности тока от напряженности сильного электрического поля будет иметь вид, представленный на рис.7.9.б.
0 – соответствует полю, при котором электроны
начинают заполнять второй минимум энергии.
На зависимости дрейфовой скорости от напряженности поля наблюдается участок с отрицательной дифференциальной подвижностью. На основе эффекта Ганна были созданы высокочастотные диоды Ганна.
64
Для получения закона дисперсии электрона в кристалле решают уравнение Шредингера в приближениях сильно связанных электронов или квазисвободных электронов. Оба приближения дают представления об общих закономерностях движения электрона в периодическом потенциальном поле кристалла. Приближение сильно связанных электронов дает более наглядное представление о физических свойствах полупроводников и позволяет
установить общий характер зависимости E k .
В приближении сильно связанных электронов решение уравнения Шредингера дает закон дисперсии электронов в кристалле в следующем виде:
|
E |
|
C A q |
n |
|
|
|
|
E k |
x |
a |
|
eikxq |
, |
(2.1) |
||
|
|
|
|
|
|
|
||
g
где Ea – дискретный уровень энергии атома; С – величина сдвига уровня Ea за счет кулоновского взаимодействия
электронов и ядер; g – номер узла кристаллической решетки; q – вектор, соединяющий соседние атомы.
A q gWr gdV – объемный обменный интеграл
V
энергии, характеризующий обменную энергию взаимодействия атомов по всему объему кристалла. V – объем кристалла; g – волновая функция электрона в g-атоме; g –
волновая функция электрона, комплексно сопряженная с g ;
Wr – энергия возмущения электрона в кристалле, равная разности потенциальных энергий электрона в кристалле и в изолированном атоме и имеет отрицательный знак.
Третий член уравнения (2.1) характеризует обменное взаимодействие между парой атомов, находящихся на расстоянии q один от другого.
9
http://www.mitht.ru/e-library
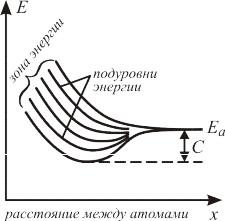
При сближении атомов перекрываются электронные оболочки (волновые функции) соседних атомов и электроны могут без изменения энергии, путем последовательных обменов соседних атомов переходить от атома к атому. Из-за обменного взаимодействия валентные электроны становятся общими (электрон пребывает на атоме ~10-15 с), уровень энергии Ea опускается на величину C и расщепляется на подуровни энергии, из которых формируется энергетическая зона, ширина которой зависит от величины A q .
Рис. 2.1. Расщепление дискретного уровня энергии Ea атома на подуровни энергии в процессе образования кристалла.
Величина обменного интеграла энергии зависит от степени перекрытия электронных оболочек (волновых функций электронов атомов), энергии возмущения и
симметрии кристаллической решетки. |
|
Границы зон определяются минимальным |
и |
|
|
максимальным значением 3-го слагаемого, в котором eikxq |
– |
некоторый структурный коэффициент, зависящий от реальной структуры кристаллов.
10
Эффективная масса электрона изотропна и является скалярной величиной. Абсолютный минимум энергии зоны проводимости единственный М=1.
Большим достоинством арсенида галлия является очень небольшая по величине эффективная масса электронов mn 0.07m0 и, следовательно, их высокая подвижность.
Ширина запрещенной зоны больше чем у кремния, при 0 К Eg 1.52 эВ, при 300 К Eg 1.43 эВ. Концентрация
собственных носителей заряда при 300 К ni≈107 cм-3. Валентная зона, также как и у простых
полупроводников, состоит из трех подзон: подзоны тяжелых дырок, легких дырок и подзоны, которая отщеплена из-за спин-орбитального взаимодействия. Эффективные массы дырок mpT 0.5m0 , mpЛ 0.12m0 , mdp 0.54m0 . Отношение эффективной массы электрона к эффективной массе тяжелых дырок равно 7.7, что приводит к большой разнице в подвижностях электронов и дырок.
Кроме того, отличительной особенностью зонной структуры арсенида галлия является близкое расположение минимума энергии Еs подзоны зоны проводимости в направлении <100> (Δ), с эффективной массой электрона mn 1.2m0 , к абсолютному минимуму энергии Еs-Ес=0,36 эВ
(рис.7.9.а). Наличие двух минимумов энергии, которые разделяет небольшой энергетический барьер, с существенно разными эффективными массами электронов, влияет на свойства, а именно, при воздействии сильного электрического поля между минимумами возможны перескоки электронов в обе стороны и поскольку эффективные массы разные, то и дрейфовые подвижности и токи будут изменяться с частотой перескоков. Этот эффект называется эффектом Ганна и используется для генерации высокочастотных сигналов.
63
http://www.mitht.ru/e-library
